相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、在郑州抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从A地出发,晚上到达B地,约定向东为正方向,当天的航行路程记录如下(单位:千米):
+14,﹣9,+8,﹣7,+13,﹣6,+12,﹣5.
(1)、救灾过程中,冲锋舟离出发点A最远处有多远?(2)、若冲锋舟每千米耗油0.5升,油箱容量为28L,求冲锋舟当天救灾过程中至少还需补充多少升油? -
2、如图,某同学设计了一种计算程序流程图,按要求完成下列任务:
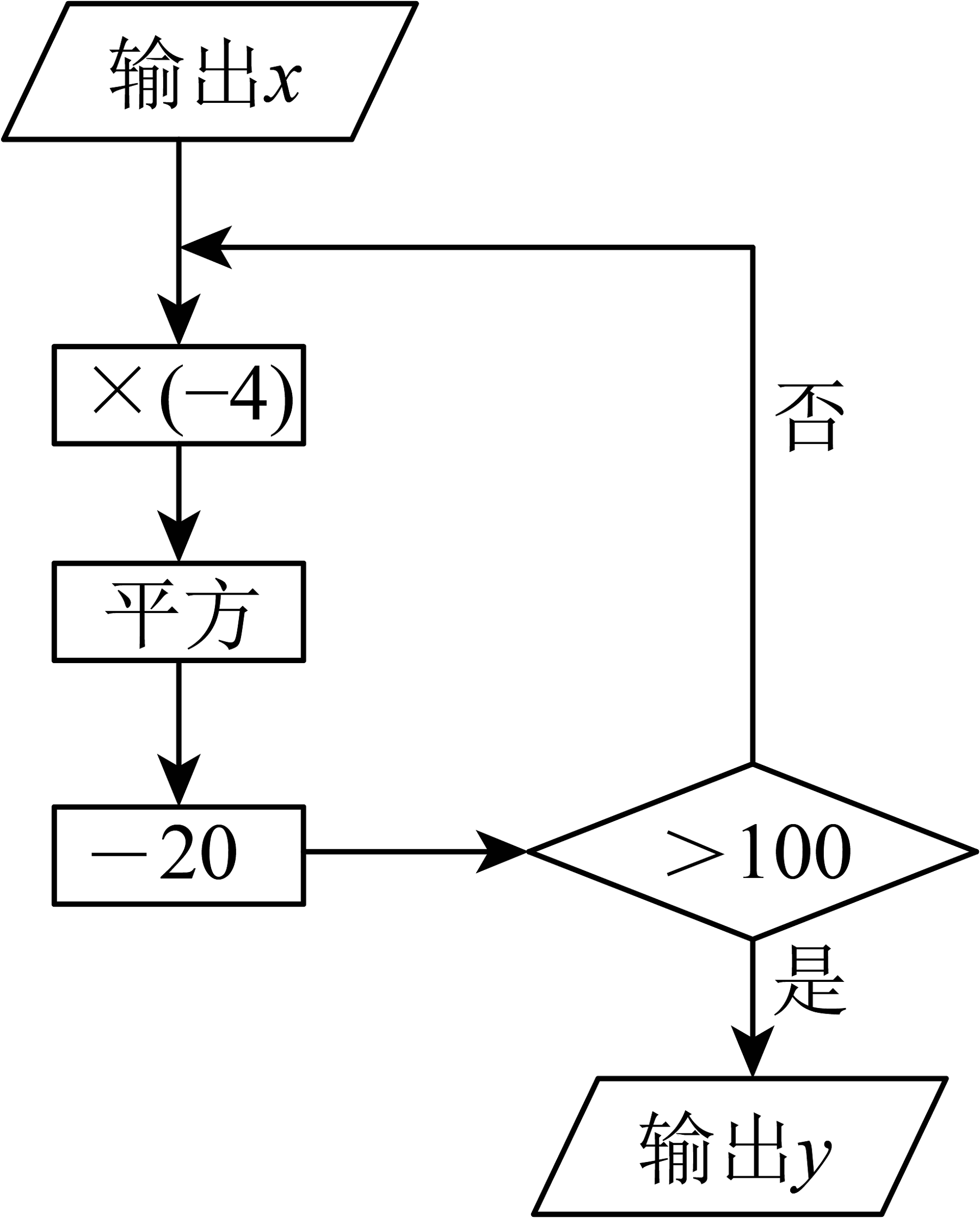 (1)、当输入的值为时,求输出的值;(2)、若输出的值为380,直接写出输入的值为__________;(3)、若输入的值为0,求输出的值.
(1)、当输入的值为时,求输出的值;(2)、若输出的值为380,直接写出输入的值为__________;(3)、若输入的值为0,求输出的值. -
3、如图所示的是某个几何体从三种不同方向所看到的图形.
(1)说出这个几何体的名称;
(2)根据图中有关数据,求这个几何体的表面积.
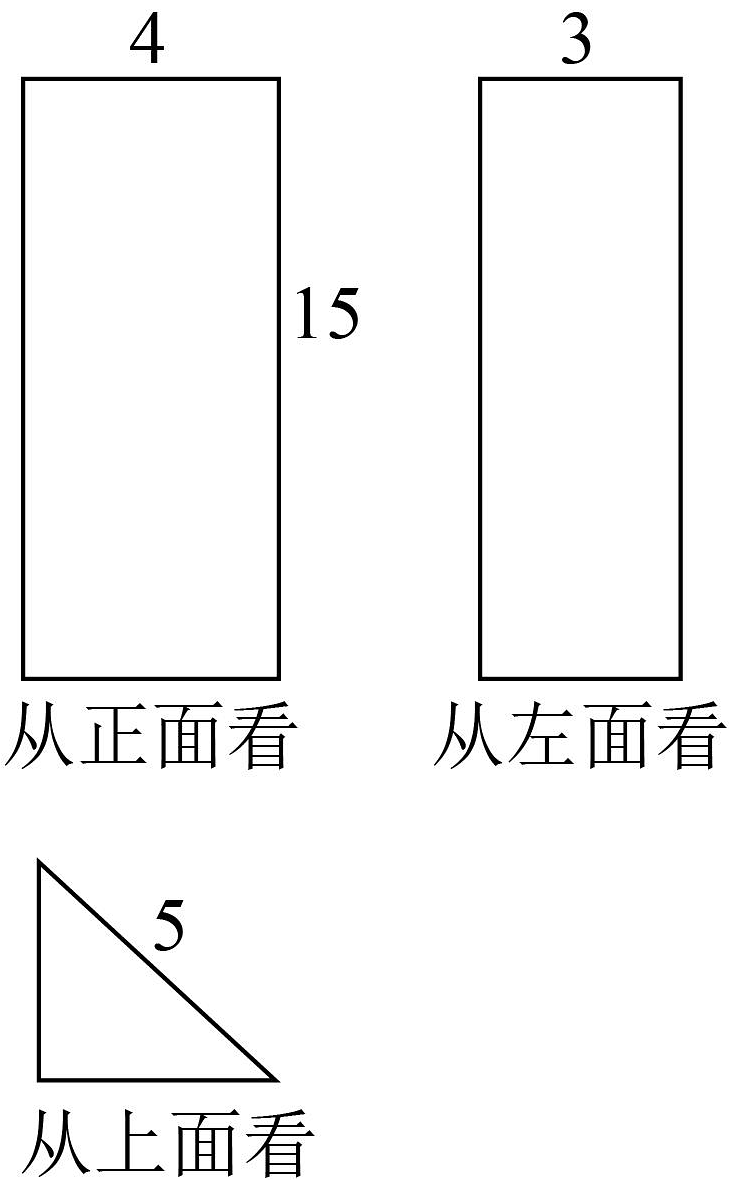
-
4、计算下列各题:(1)、(2)、(3)、(4)、
-
5、如图,10个大小相同的小立方块搭成一个几何体,在保持从正面看和从左面看到的形状图不变的情况下,最多可以拿掉个小立方块.

-
6、一个物体的主视图、左视图、俯视图都相同,这个几何体可能的形状是 . (至少2种)
-
7、点A在数轴上,点A所对应的数用表示,且点A到原点的距离等于8,则a的值为 .
-
8、直播购物成为一种新的购物方式,官方数据显示,某直播间累计观看人数达到了万,则万用科学记数法表示为 .
-
9、一只小球落在数轴上的某点处,第一次从处向右跳1个单位到处,第二次从向左跳2个单位到处,第三次从向右跳3个单位到处,第四次从向左跳4个单位到处…,若小球按以上规律跳了次时,它落在数轴上的点处所表示的数恰好是 , 则这只小球的初始位置点所表示的数是( )A、 B、 C、 D、
-
10、如果 , , 且 , 那么( )A、 B、 C、或 D、或1
-
11、在、、、、 , 负数有( )个.A、2 B、3 C、4 D、5
-
12、2024年巴黎奥运会上中国体育代表团获得40枚金牌,金牌数与美国队并列第一,创造了参加境外奥运会的最佳战绩.下列各组巴黎奥运会的项目图标中,是全等形的是( )A、
 B、
B、 C、
C、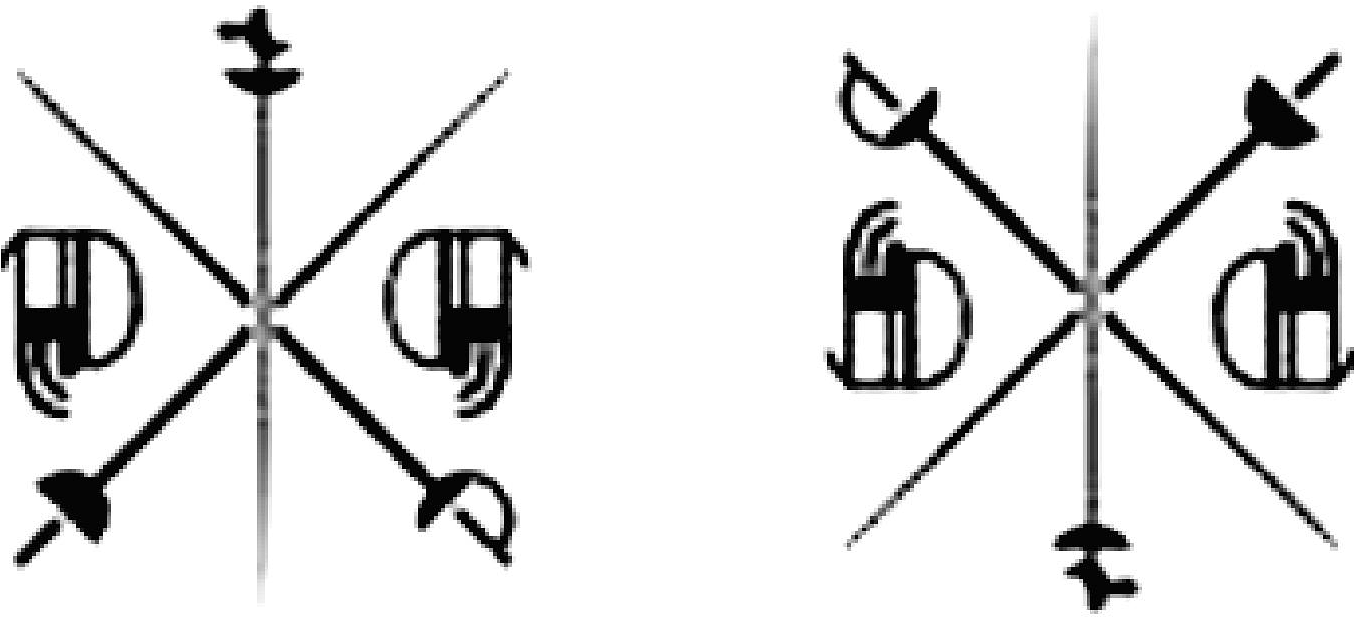 D、
D、
-
13、在等边三角形ABC中,点E为线段AB上一动点,点E与A,B不重合,点D在CB的延长线上,且ED=EC.
 (1)、当E为边AB的中点时,如图1所示,确定线段AE与BD的大小关系,并证明你的结论;(2)、如图2,当E不是边AB的中点时,(1)中的结论是否成立?若不成立,请直接写出BD与AE的数量关系;若成立,请给予证明;(提示:过E作交AC于点F)(3)、在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,的边长为1,AE=2,请直接写出CD的长.
(1)、当E为边AB的中点时,如图1所示,确定线段AE与BD的大小关系,并证明你的结论;(2)、如图2,当E不是边AB的中点时,(1)中的结论是否成立?若不成立,请直接写出BD与AE的数量关系;若成立,请给予证明;(提示:过E作交AC于点F)(3)、在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,的边长为1,AE=2,请直接写出CD的长. -
14、(1)如图①,点D、A、B在一条直线上, , , . 求证:;
(2)如图②,在中,于点G,以点A为直角顶点,分别以、为直角边,向外作等腰直角三角形和等腰直角三角形 , 过点E、F作射线的垂线,垂足分别为点P、Q,与之间有怎样的数量关系?证明你的结论.

-
15、已知, , , .
 (1)、如图①,求证:;(2)、如图②,与相交于点O,若点E是的中点,求证: .
(1)、如图①,求证:;(2)、如图②,与相交于点O,若点E是的中点,求证: . -
16、已知:线段、交于O,为钝角, , 于F,于E, . 求证: .

-
17、已知: , , , . 求证: .

-
18、如图,B处在A处的南偏西方向,C处在A处的南偏东方向,C处在B处的北偏东方向,则 .

-
19、如图,在中,和的平分线相交于点 , 过点作EFBC交于 , 交于 , 过点作于 , 下列选项中结论错误的是( )
 A、 B、 C、点到各边的距离相等 D、设 , , 则
A、 B、 C、点到各边的距离相等 D、设 , , 则 -
20、如图中, , , , 则=( )
 A、 B、 C、 D、
A、 B、 C、 D、