相关试卷
- 2017-2018学年北师大版数学八年级下册同步训练:6.4 多边形的内角和与外角和
- 2017-2018学年北师大版数学八年级下册同步训练:6.3 三角形的中位线
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.2 平行四边形的判定 ——用对角线的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.1 平行四边形的判定——用边的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.4分式方程课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.4 分式方程课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时1
-
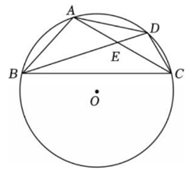
1、如图,四边形ABCD的外接圆⊙O的半径为5,对角线AC与BD的交点E,AE=EC,AB=AE,且BD=8,则四边形ABCD的面积为.
-
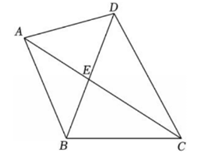
2、如图,已知 , , , , , 则
-
3、已知正数a,b满足 , 则的最小值为.
-
4、已知n为正整数,则末尾最多有个0.
-
5、已知a为正整数,若关于x的方程x4+(a+5)x3+(3a+10)x2-4a-16=0有四个互不相同的整数根,则a=.
-
6、若抛物线y=x2+bx+c与x轴、y轴交于三个不同的点A、B、C,当实数b、c变化时,△ABC的外接圆一定经过定点,此定点的坐标为.
-
7、在平面直角坐标系xOy中,抛物线y=-x2+4x与x轴的正半轴交于点A,其顶点为M,点P是该抛物线上位于A、M两点之间的部分上的动点,过点P作PB⊥x轴于点B,PC⊥y轴于点C,且交抛物线于点D,连接BC,AD,OP,当四边形ABCD被OP分成的两部分面积比为1:2时,点P的坐标为.

-
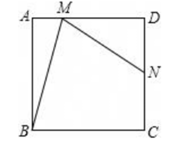
8、在正方形ABCD中,N是DC的中点,M是AD上异于D的点,且∠NMB=∠MBC,则tan∠ABM的值为.
-
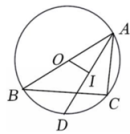
9、 AB为⊙O的直径,C为⊙O上一点,I为△ABC内心,AI与⊙O交于点D,OI⊥AD与点I,CD=4,则AC=.
-
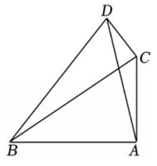
10、如图,∠BAC=∠BCD=90°,AC=2,三角形BCD面积始终为2,则AD的最大值为.
-
11、如图,△ABC是⊙O的内接三角形,将劣弧沿AC折叠后刚好经过弦BC的中点D.若AC=6,∠C=60°,则⊙O的半径长为.

-
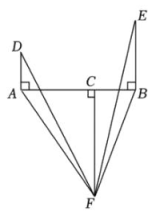
12、如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=53°,则∠DFE的度数是多少?
-
13、试求方程x2-2x-4|x-1|+4=0的四个根之和;当t<5时,再求方程x2-2x-4|x-1|+b=0的四个根之和.
-
14、已知a,b,c是三个非负数,并且满足3a+2b+c=5,2a+b-3c=1,设m=3a+b-7c,则m的最大值为.
-
15、已知x2+3x+1=0,则-8x+2025=.
-
16、已知a、b、c是实数,若(x2+2x+3)(3x2+4x-5)+(x2+x-4)2=(ax2+bx+lcl)2 , 则代数式a+20b+23|c|的值为( )A、0 B、1 C、-39 D、85
-
17、如果方程的三根可作为一个三角形的三边之长,则实数m的取值范围是( )A、 B、 C、 D、
-
18、已知 , , 则.
-
19、如图,在△ABC中,CB>AC,∠BAC=α,∠ABC=β,D为AB上一点,且CB-CA=BD,I为△ABC的三条角分线交点,则∠IDA=( )
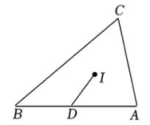 A、 B、 C、β D、
A、 B、 C、β D、 -
20、已知方程2|x|-k=kx-3无负数根,那么k的取值范围是( )A、-2≤k≤3 B、2<k≤3 C、2≤k≤3 D、k≥3或k≤2