相关试卷

1、如图，已知AB是⊙O的直径，弦DC⊥AB 于点E， G是AC上一点， AG， DC的延长线交于点 F. 连结AD， GC.

(1)、如图1，若E为半径OB的中点. 求∠DAB的度数.

(2)、连结DG. 求证： ∠AGD=∠CGF.

(3)、若∠F=30°， CG=2 $\sqrt{6}$ ， ⊙O 的半径为6. 求弦AD的长.

查看解析
2、已知二次函数 $y = x^{2} - (2 m - 1) x + m^{2} - m$ （m 是常数，且 m≠0）

(1)、证明：不论 m 取何值，该二次函数图象总与 x 轴有两个交点.

(2)、若.A（n-3， n²+2）， B（-n+1， n²+2）是该二次函数图象上的两个不同点，求二次函数表达式和 n 的值.

(3)、在（2）的条件下，若点 C（x₀y₁），点D （x₀+1，y₂）也均在此函数图象上，且满足y₁≥y₂ ，求x₀的取值范围.

查看解析
3、课堂上，老师组织同学们一起研究二次函数y=2（x+m-4）（x-m+2）的最值问题.

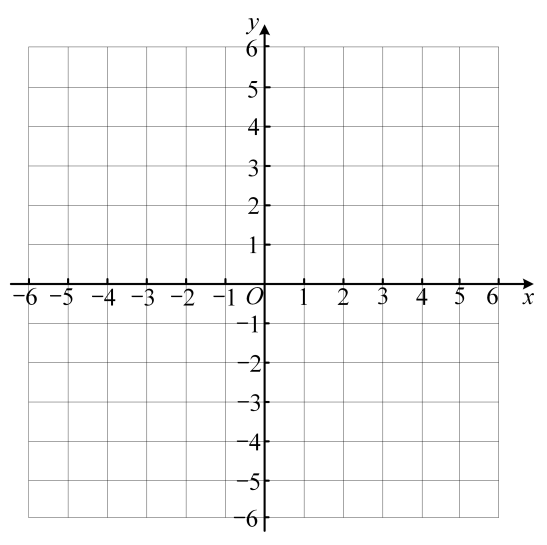
(1)、当m = 2时，
①画出函数的图象，并求出该二次函数的最值.
②根据函数图象，直接写出当0≤x<3时，y的取值范围。

(2)、当m取不同值时，函数的最小值会随之发生变化.小阳认为，这些最小值里面存在一个最大值，这个最大值为0.你认为小阳的想法是否正确?请说明理由.

查看解析
4、如图，在△ABC中， AB=AC，⊙O是△ABC的外接圆， BO的延长线交边AC于点 D.

(1)、求证： ∠BAC=2∠ABD.

(2)、若⊙O的半径为5，当∠ABD=30°时，求BC的长.

查看解析
5、如图， AB是⊙O的直径，四边形ABCD 内接于⊙O， OD交AC于点.E， $\hat{A D} = \hat{C D} .$

(1)、求证： OD∥BC；

(2)、若AC=12， DE=4，求⊙O的半径.

查看解析
6、 “保护环境，建设美好校园”是某校环保社团的宗旨，该社团要从学校4名同学：小航（女）、小舟（女）、小西（男）、小胡（男）中随机选取若干名成为校园环境“小卫士”，且每名同学被选中的可能性都相同.

(1)、若随机选取1名同学成为校园环境“小卫士”，则小西初选中的概率为；

(2)、若随机选取2名同学成为校园环境“小卫士”，请用树状图法或列表法求选中的两名学生恰好是一男一女的概率.

查看解析
7、如图，AB是半圆O的直径，点C为半圆O上一动点（除点A，B外），若圆弧BC沿BC所在的直线折叠后与直径AB交于点D，当AB=10， OD=3时，折痕BC=

查看解析
8、若二次函数 $y = 2 {(x + 1)}^{2} + 3$ 的图象上有三个不同的点， $A (x_{1}, 4) 、 B (x_{1} + x_{2} - 2, n) 、 C (x_{2}, 4),$ 则n的值为 .

查看解析
9、已知⊙O的半径为10cm，弦AB∥CD， AB=12cm， CD=16cm，则AB 与CD间的距离为.

查看解析
10、已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，则关于x的不等式 $a x^{2} + b x + c ＞$ 0（a≠0）的解集为.

查看解析
11、如图， A、B、C是⊙O上的三个点，若∠AOC=68°，则∠B=.

查看解析
12、如表是一位同学在罚球线上投篮的试验结果，根据表中数据回答问题：
试验总次数
100
200
300
500
1500
2000
3000
投中的次数
61
93
165
246
753
996
1503
投中的频率
0.610
0.465
0.550
0.492
0.502
0.498
0.501
根据表中的数据，估计这位同学投篮一次，投中的概率为.（保留一位小数）

查看解析
13、在平面直角坐标系中，如果点 P 的横坐标和纵坐标互为相反数，则称点 P 为“美丽点”.例如：点（1，-1），（-2， 2），（ $\sqrt{3}$ ， - $\sqrt{3}$ ）， ….都是“美丽点”.若二次函数 $y = a x^{2} + 3 x + 1 (a \neq 0)$ 的图象上有且只有一个“美丽点”，且当 -2≤x≤m时，函数 $y = (a - 1) x^{2} + 3 x + 1 (a \neq 0)$ 的最小值为 $\frac{1}{4}$ ，最大值为7，则m的取值范围是（.

A、 $m \leq - \frac{1}{2}$ B、 $m \geq - \frac{1}{2}$ C、 $- \frac{1}{2} \leq m \leq 1$ D、 $- \frac{1}{2} < m < 1$

查看解析
14、如图， AB是⊙O 的直径， CD是⊙O的弦， AB⊥CD于点E， OE=DE=2，点F是⊙O上一动点，连接CF，DF，点G是DF的中点，连接EG，当线段EG取得最大值时，点G到弦 CD的距离是（）

A、 $\frac{5}{2}$ B、2 C、 $\sqrt{2}$ D、 $1 + \sqrt{2}$

查看解析
15、已知二次函数 $y = {(x + 1)}^{2} - n$ 的图象上有三点A （1， y₁）， B （2， y₂）， C （-2， y₃），则y₁ ， y₂ ， y₃的大小关系为（）

A、y₁>y₂>y₃ B、y₂>y₁>y₃ C、y₃>y₁>y₂ D、y₃>y₂>y₁

查看解析
16、如图，以量角器的直径AB为斜边画直角三角形ABC，量角器上点D对应的读数是 $10 0^{\circ},$ 则 $∠ B C D$ 的度数为（）

A、40° B、45° C、50° D、80°

查看解析
17、下列说法中正确的是（）

A、三点确定一个圆 B、相等的圆心角所对的弧相等 C、过弦的中点的直径平分弦所对的两条弧 D、相等的弧所对的圆心角相等

查看解析
18、已知点A是⊙O外一点，且⊙O的半径为5，则OA 的长可能为（）

A、3 B、4 C、5 D、6

查看解析
19、盒子里有10个球，它们只有颜色不同，其中红球有6个，黄球有3个，黑球有1个.小军从中任意1一个球，下面说法正确的是（）

A、一定是红球 B、摸出红球的可能性最大 C、不可能是黑球 D、摸出黄球的可能性最小

查看解析
20、定义：如果一个三角形的三边长分别为a，b，c，且满足 $a^{2} + b^{2} = 2 c^{2},$ 那么称这个三角形为优美三角形。

(1)、判断等边三角形是不是优美三角形，并说明理由。

(2)、如图，在△ABC 中， $A B = A C = 3, B C = \sqrt{3},$ 在 AC 上取一点 D，使得 $A D = \frac{1}{2} C D,$ 连结 BD。求证：△ABD 是优美三角形。

查看解析

上一页 344 345 346 347 348 下一页跳转

试验总次数	100	200	300	500	1500	2000	3000
投中的次数	61	93	165	246	753	996	1503
投中的频率	0.610	0.465	0.550	0.492	0.502	0.498	0.501