相关试卷
- 2017-2018学年人教版数学七年级下册同步训练: 10.3《课题学习 从数据谈节水》
- 广东省韶关市2017-2018学年七年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年九年级上学期数学期末考试试卷
- 广东省韶关市2017-2018学年八年级上学期数学期末考试试卷
- 2017-2018学年人教版数学八年级下册同步训练:19.1.2《函数图像》
- 2017-2018学年人教版数学八年级下册同步训练: 20.3《体质健康测试中的数据分析》
- 2017-2018学年人教版数学八年级下册同步训练: 20.2《数据的波动程度》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.2《中位数和众数》
- 2017-2018学年人教版数学八年级下册同步训练: 20.1.1《平均数》
- 2017-2018学年人教版数学八年级下册同步训练:19.2.3《一次函数与方程、不等式》
-
1、某公路养护小组乘车沿一条南北向公路巡视养护,某天早晨他们从A地出发,晚上最终到达B地.约定向北为正方向,当天汽车的行驶记录(单位:)如下表所示.
第一次
第二次
第三次
第四次
第五次
第六次
第七次
第八次
(1)、汽车在巡视过程中,第______次离A地最远,最远距离为______;(2)、B地在A地的哪个方向,B地与A地相距多少千米?(3)、如果汽车行驶平均耗油 , 那么这天汽车共耗油多少升? -
2、先化简再求值: , 其中x,y满足 .
-
3、计算:(1)、;(2)、 .
-
4、把下面的有理数填入它们属于的集合内:15, , , , , 10, , , .(1)、整数集合:{ …}(2)、正有理数集合:{ …}(3)、负有理数集合:{ …}(4)、负分数集合:{ …}
-
5、如图,把半径为1的圆形纸片放在数轴上,圆形纸片上的A点对应2,将圆形纸片沿着数轴无滑动的逆时针滚动一周,点A到达点的位置,则点表示的数是 .

-
6、若 , 则的值为 .
-
7、我们把称为有理数()的差倒数,如:的差倒数是 . 如果 , 是的差倒数,是的差倒数,是的差倒数,…,以此类推,那么的值是( )A、 B、 C、 D、
-
8、当输入的值为时,按如图所示的程序运算,则输出的是( )
 A、1 B、3 C、 D、5
A、1 B、3 C、 D、5 -
9、如图,将按某种方式填入下图的圈内,使横、竖以及内、外两圈上的4个数字之和都相等,则a,b所在位置的两个数字之和是( )
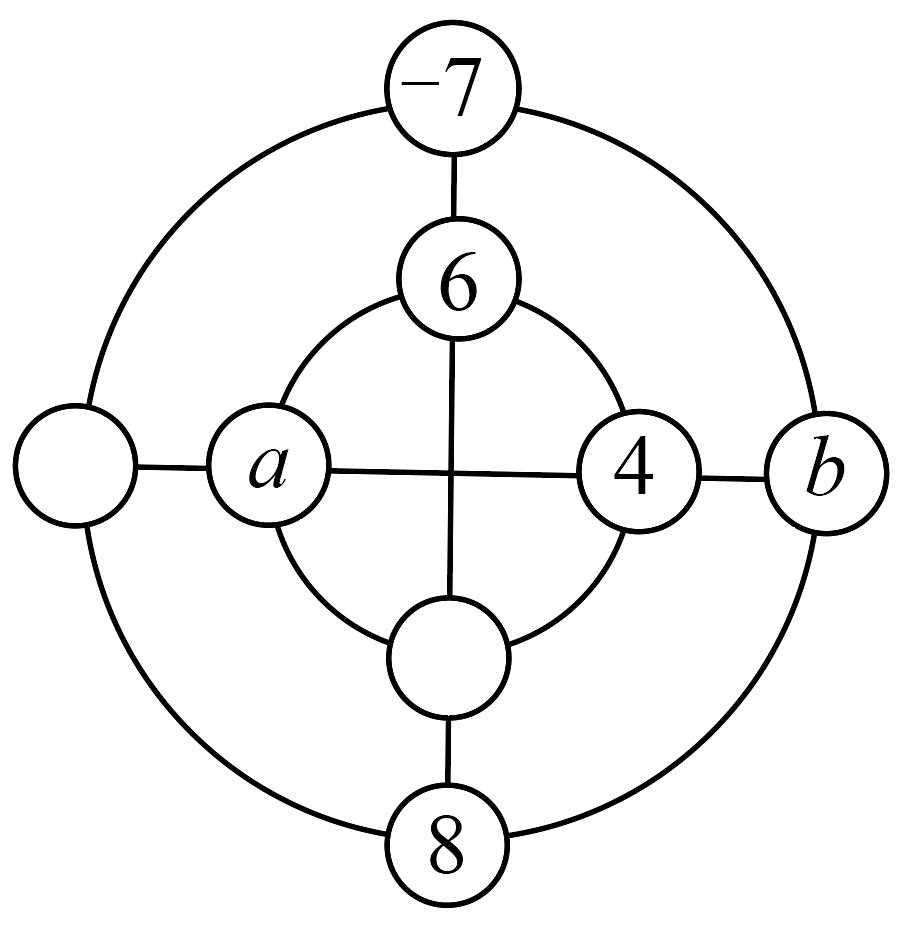 A、或 B、或 C、或 D、或
A、或 B、或 C、或 D、或 -
10、随着游戏《黑神话:悟空》话题热度持续上涨,山西作为游戏中取景地最多的省份,古建打卡热度在国庆假期达到新高.国庆期间,游戏涉及的山西个文物景点累计门票收入万元.数据“万”可用科学记数法表示为( )A、 B、 C、 D、
-
11、一个三位数,个位数字是 , 十位数字是 , 百位数字是 , 则这个三位数用代数式表示为( )A、abc B、 C、 D、
-
12、算式“”可以简便的表示为:( )A、 B、 C、 D、
-
13、如图,若点所表示的数分别为 , 则的大小关系为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、计算:( )A、 B、 C、5 D、
-
15、如图,已知数轴上的点A表示的数是6,点B是数轴上在A左侧的一点,且A、B两点间的距离为10个单位长度.动点P从点A出发,以每秒4个单位长度的速度沿数轴向左运动,设运动时间为秒.
 (1)、数轴上点B表示的数是 ;(2)、动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左运动,若点P、Q同时出发.
(1)、数轴上点B表示的数是 ;(2)、动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左运动,若点P、Q同时出发.①当点P运动多少秒时,点P追上点Q?
②当点P运动多少秒时,点P与点Q之间的距离为8个单位长度?
-
16、某校七年级准备组织学生到某社会实践基地参加社会实践活动,门票价为每人20元,由各班班长负责买票.“下面是1班班长与售票员咨询的对话:”
 (1)、1班学生人数为44,选择了方案一购票,1班购票需要______元;(2)、2班选择了方案二,购票费用为702元,求2班有多少人?(3)、3班买票时方案一和方案二的购票费用相同,3班有多少人?
(1)、1班学生人数为44,选择了方案一购票,1班购票需要______元;(2)、2班选择了方案二,购票费用为702元,求2班有多少人?(3)、3班买票时方案一和方案二的购票费用相同,3班有多少人? -
17、定义:如果两个一元一次方程的解之和为1,我们就称这两个方程为“美好方程”.
例如:方程和为“美好方程”.
(1)、方程与方程是“美好方程”吗?请说明理由;(2)、若关于的方程与方程是“美好方程”,求的值. -
18、请根据图示的对话解答下列问题:
 (1)、分别求出a和b的值;(2)、已知 , 求的值.
(1)、分别求出a和b的值;(2)、已知 , 求的值. -
19、如图,将边长为a的正方形按虚线剪成4个部分,去掉其中边长为b的小正方形,将剩余的3个部分重新拼成一个互不重叠且无缝隙的长方形.

问题:
(1)、请在图②中标注相应的数据;(2)、求拼好后长方形的周长;(3)、若 , , 求拼好后长方形的面积. -
20、轮船沿江从A港顺流行驶到B港,比从B港返回A港少用2h,船在静水中的速度为 , 水速为 .(1)、船在顺水中的速度为__________;船在逆水中的速度为__________;(2)、求A港和B港的距离是多少?