-
1、二次函数的部分图象如图所示,其对称轴为直线 , 且与x轴的一个交点坐标为 . 下列结论:;;;关于的一元二次方程有两个不相等的实数根.其中正确结论的个数是( )
 A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个 -
2、如图,若被击打的小球飞行高度h(单位:)与飞行时间t(单位:)具有函数关系为 , 则小球从飞出到落地的所用时间为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、如图,在平面首角坐标系中,点A,C在x轴上,点C的坐标为 , . 将先绕点C顺时针旋转 , 则变换后点A的对应点坐标是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
5、我们不妨约定:对角互补的凸四边形叫做“互补四边形”.根据约定,解答下列问题.
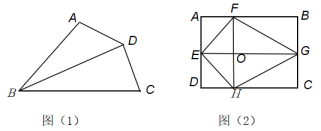 (1)、试判断下列图形一定为“互补四边形”?若是,请在括号内划“”;若不是,请在括号内划“”.
(1)、试判断下列图形一定为“互补四边形”?若是,请在括号内划“”;若不是,请在括号内划“”.①平行四边形( );②矩形( );③正方形( ).
(2)、如图(1),在四边形中,对角线平分∠ABC,DA=DC,AB<CB.求证:四边形是“互补四边形”.(3)、如图(2),若□ABCD是“互补四边形”,点是□ABCD内部一个动点,且不与四边重合,过动点作的平行线,交□ABCD的边于点连接 , AB=8,AD=6.当点运动时,求四边形周长的最小值. -
6、如果关于的一元二次方程有两个实数根,其中一个实数根是另一个实数根的3倍,那么称这样的方程是“3倍根方程”.例如一元二次方程的两个根是 , 则方程 是“3倍根方程”.(1)、通过计算,判断是否是“3倍根方程”.(2)、若关于x的方程是“3倍根方程”,求代数式的值;(3)、已知关于x的一元二次方程(是常数)是“3倍根方程”,请写出的值.
-
7、已知,如图,在中, , D是的中点, 连接 , F是的中点,过点C作交的延长线于点E,连接 .
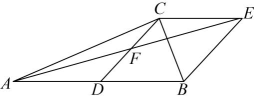 (1)、求证:四边形是菱形.(2)、若∠CAB=30 , AB=8,求菱形CDBE的面积.
(1)、求证:四边形是菱形.(2)、若∠CAB=30 , AB=8,求菱形CDBE的面积. -
8、为进一步发展基础教育,自 2023年以来,某县加大了教育经费的投入,2023年该县投入教育经费 7000万元,2025年投入教育经费 10080万元.假设该县这两年投入教育经费的年平均增长率相同.(1)、求这两年该县投入教育经费的年平均增长率;(2)、若该县教育经费的投入还将保持相同的年平均增长率,请你预算 2026 年该县投入教育经费多少万元.
-
9、 学校组织七、八年级学生参加了“国家安全知识”测试,已知七、八年级各有人,现从两个年级分别随机抽取名学生的测试成绩(单位:分)进行统计:
七年级:86 94 79 84 71 90 76 83 90 87
八年级:88 76 90 78 87 93 75 87 87 79
整理如下:
年级
平均数
中位数
众数
方差
七年级
84
a
90
44.4
八年级
84
87
b
36.6
根据以上信息,回答下列问题:
(1)、填空:a= , ;(2)、A同学说:“这次测试我得了分,位于年级中等偏上水平”,由此可判断他哪个年级的学生,并说明理由;(3)、学校规定测试成绩不低于分为“优秀”,估计该校这两个年级测试成绩达到“优秀”的学生总人数. -
10、解方程:(1)、(2)、 .
-
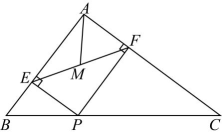
11、如图6,在直角三角形ABC中,AB=3,AC=4,BC=5,P为边上一动点,于 , 于 , 为的中点,则的最小值为 .
-
12、设x1 , x2是一元二次方程x2-2x-1=0的两根,则.
-
13、如果菱形的两条对角线的长分别为a和b,且a,b满足 , 那么菱形的面积等于 .
-
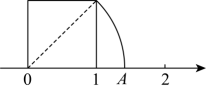
14、把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A , 则点A对应的数是 .
-
15、经过点(2,﹣3)的正比例函数的解析式为 .
-
16、函数中,自变量x的取值范围是 .
-
17、已知函数y=kx+b的图象如图3所示,则函数y=-bx+k的图象大致是( )
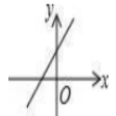 A、
A、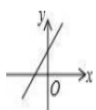 B、
B、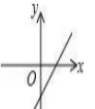 C、
C、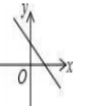 D、
D、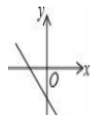
-
18、 如图,在直角三角形中, , , , 为直角三角形ABC的中线,则的长为( )
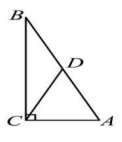 A、 B、 C、 D、
A、 B、 C、 D、 -
19、 已知关于x的一元二次方程x2-2x=m有两个不相等的实数根,则m的取值范围是( )A、m<1 B、m<-2 C、m=0 D、m>-1
-
20、 如图,在矩形中, , 相交于点.若的面积为2,则矩形的面积为( )
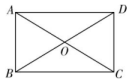 A、4 B、6 C、8 D、10
A、4 B、6 C、8 D、10