相关试卷

1、下列二次函数图象与 $y = x^{2}$ 的开口大小、方向、形状完全相同的是（）

A、 $y = x^{2} + 1$ B、 $y = - {(x - 1)}^{2}$ C、 $y = 2 x^{2}$ D、 $y = - x^{2} + 1$

查看解析
2、如图，在 $△ A B C$ 中， $∠ C = 30 °$ ， $A D ⊥ A B$ ，垂足为点 $A$ ，交 $B C$ 于点 $D$ ，过点 $D$ 的直线 $m$ 恰好垂直平分线段 $A C$ ， $A D = 3$ ，则 $B C$ 的长是（）．

A、 $6$ B、 $9$ C、 $12$ D、 $18$

查看解析
3、【阅读理解】
我们知道，任意两点关于它们所连线段的中点成中心对称，在平面直角坐标系中，任意两点 $P (x_{1}, y_{1})$ ， $Q (x_{2}, y_{2})$ 的对称中心的坐标为 $(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$
【观察应用】
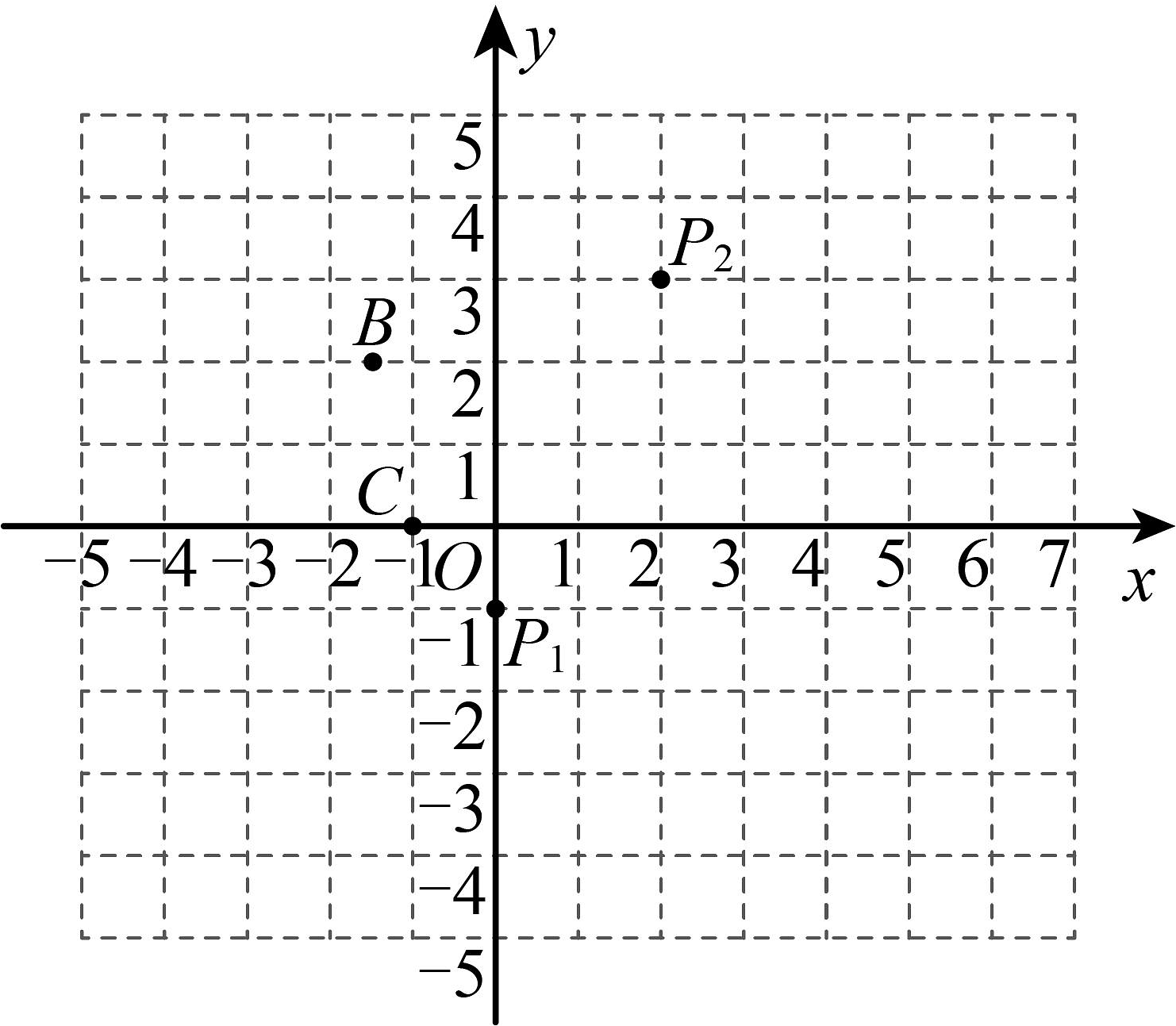
（1）如图，在平面直角坐标系中，若点 $P_{1} (0, - 1)$ ， $P_{2} (2, 3)$ 的对称中心是点 $A$ ，则点 $A$ 的坐标为；
（2）另取两点 $B (- 1.6, 2.1)$ ， $C (- 1, 0)$ ．有一电子青蛙从点 $P_{1}$ 处开始依次关于点A，B，C做循环对称跳动，即第一次跳到点 $P_{1}$ 关于点A的对称点 $P_{2}$ 处，接着跳到点 $P_{2}$ 关于点B的对称点 $P_{3}$ 处，第三次再跳到点 $P_{3}$ 关于点C的对称点 $P_{4}$ 处，第四次再跳到点 $P_{4}$ 关于点A的对称点 $P_{5}$ 处，……则 $P_{3}$ ， $P_{8}$ 的坐标分别为；
【拓展延伸】
（3）求出点 $P_{2023}$ 的坐标，并直接写出在x轴上与点 $P_{2023}$ ，点 $C$ 构成等腰三角形的点的坐标．

查看解析
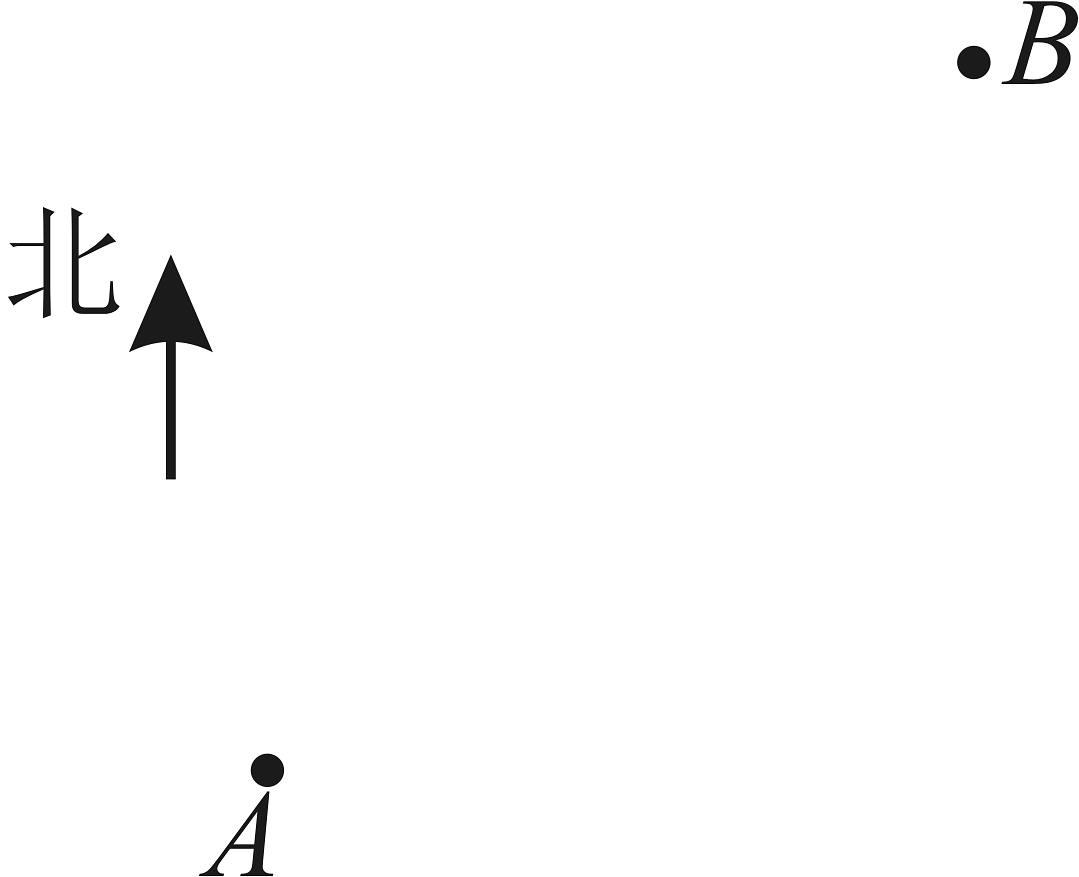
4、如图所示，这是某市地图的一部分，分别以正东，正北方向为x轴，y轴的正方向建立直角坐标系，规定一个单位长度表示 $1 km$ ，甲、乙两人对着地图如下描述A处的位置．
甲：A处的坐标是 $(8, 0)$ ；乙：A处在B处南偏西 $45 °$ 方向，相距 $16 \sqrt{2} km$ ．求B处的坐标．

查看解析
5、如图，正方形 $A B C D$ 的边长为 $6$ ， $A D ∥ y$ 轴， $A (1, 4)$ ．

(1)、写出 $B$ ， $C$ ， $D$ 三个顶点的坐标；

(2)、写出 $C D$ 中点 $P$ 的坐标．

查看解析
6、交通规则上有许多标志，如图 $①$ 所示是某地的两个限制数量，某货车的迎面的截面图形坐标如图 $②$ 所示，问该车能否通过此路段，并说明理由．

查看解析
7、计算．

(1)、 $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$

(2)、 ${(\sqrt{2} + \sqrt{3})}^{2} + (\sqrt{2} - 2 \sqrt{3}) (2 \sqrt{3} + \sqrt{2})$

查看解析
8、在 $△ A B C$ 中， $∠ C = 90 °$ ，设 $A B = c$ ， $B C = a$ ， $A C = b$ ．

(1)、已知 $a = 8$ ， $b = 15$ ，求c；

(2)、已知 $c = 13$ ， $b = 5$ ，求a．

查看解析
9、在平面直角坐标系 $x O y$ 中，横、纵坐标都是整数的点叫做整点．已知点A的坐标为 $(2, 4)$ ，点B的坐标为 $(1, 1)$ ，点C为第一象限内的整点．若不共线的A，B，C三点构成轴对称图形，满足题意的点C的个数为．

查看解析
10、如图是一足球场的半场平面示意图，已知球员A 的位置为 $(- 1, - 1)$ ，球员C的位置为 $(0, 1)$ ，则球员B的位置为．

查看解析
11、若规定一种运算为： $a ★ b = \sqrt{2} \times (b - a)$ ，如 $3 ★ 5 = \sqrt{2} \times (5 - 3) = 2 \sqrt{2}$ ，则 $\sqrt{2} ★ \sqrt[3]{8} =$ ．

查看解析
12、对于直角坐标平面内的任意两点 $A (x_{1}, y_{1}), B (x_{2}, y_{2})$ ，定义它们之间的一种“距离”：
$||A B|| = |x_{2} - x_{1}| + |y_{2} - y_{1}|$ ．给出下列三个命题：
①若点C在线段 $A B$ 上，则 $||A C|| + ||C B|| = ||A B||$ ；
②在 $△ A B C$ 中，若 $∠ C = 90 °$ ，则 ${||A C||}^{2} + {||C B||}^{2} = {||A B||}^{2}$ ；
③在 $△ A B C$ 中， $||A C|| + ||C B|| > ||A B||$ ．其中真命题的个数为（　　）

A、0 B、1 C、2 D、3

查看解析
13、将△ABC各顶点的横坐标都乘以﹣1，纵坐标不变，顺次连接这三个点，得到另一个三角形，下列选项正确的是（　　）

A、 B、 C、 D、

查看解析
14、点P(－m＋2，m－1)在y轴上，则点P的坐标为(　　)

A、(0，－2) B、(1，0) C、(0，1) D、(0，2)

查看解析
15、如图，点P是平面坐标系内一点，则点P到原点的距离是（）

A、3 B、 $\sqrt{2}$ C、 $2 \sqrt{2}$ D、 $\sqrt{7}$

查看解析
16、如图，在直角坐标系中卡片盖住的数可能是(　　)

A、(2，3) B、(－2，1) C、(－2，－2.5) D、(3，－2)

查看解析
17、点A的位置如图所示，则关于点A的位置，下列说法中最准确的是（）

A、距点O $4 km$ 处 B、北偏东 $30 °$ 方向上 $3 km$ 处 C、在点O北偏东 $60 °$ 方向上 $3 km$ 处 D、在点O北偏东 $30 °$ 方向上 $3 km$ 处

查看解析
18、下列各组数中是勾股数的是（）

A、3，3，5 B、4，6，8 C、7，24，25 D、6，12，13

查看解析
19、如图，点 $A, B$ 在数轴上，点 $C$ 表示 $- 3.5$ ，点 $D$ 表示 $|- 2|$ ．

(1)、点 $A$ 表示________，点 $B$ 表示________；

(2)、在数轴上表示出点 $C$ 和点 $D$ ；

(3)、用“ $<$ ”把点 $A, B, C, D$ 表示的数连接起来．

查看解析
20、【问题背景】
如图1，已知正方形 $A B C D$ 的边长为 $3$ ，点 $E$ 是边 $A B$ 上的一点，把 $△ A D E$ 沿直线 $D E$ 对折后，点 $A$ 落在点 $F$ 处．
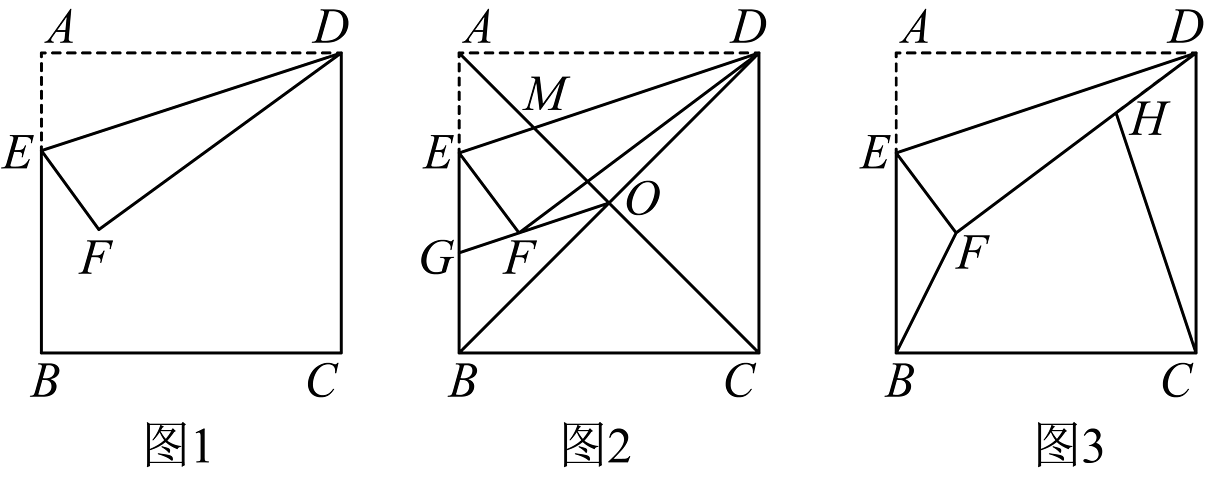
【问题探究】
（1）如图2，当 $A E = 1$ 时，正方形的对角线 $A C$ 与 $D E$ 相交于点 $M$ ，与正方形另一条对角线 $B D$ 相交于点 $O$ ，连接 $O F$ 并延长，交线段 $A B$ 于点 $G$ ．
①证明点 $M$ 是 $O A$ 的中点；
②试探究 $O G$ 与 $D E$ 有怎样的关系，并说明理由．
【拓展延伸】
（2）如图3，点 $H$ 是线段 $D F$ 上的一点，且 $D H = 1$ ，连接 $B F$ 、 $C H$ ．在点 $E$ 从点 $A$ 运动到点 $B$ 的过程中，求 $B F + C H$ 的最小值．

查看解析

上一页 1152 1153 1154 1155 1156 下一页跳转