-
1、比较大小: .
-
2、如图,在中,长为 , 长为 , 在中,长为 , 正方形的面积为

-
3、的平方根是;的相反数是 .
-
4、如图,在平面直角坐标系中,点 . 点第次向上跳动个单位长度至点 , 紧接着第次向左跳动个单位长度至点 , 第次向上跳动个单位长度至点 , 第次向右跳动个单位长度至点 , 第次又向上跳动个单位长度至点 , 第次向左跳动个单位长度至点……照此规律,点第次跳动至点 , 则点的坐标是( )
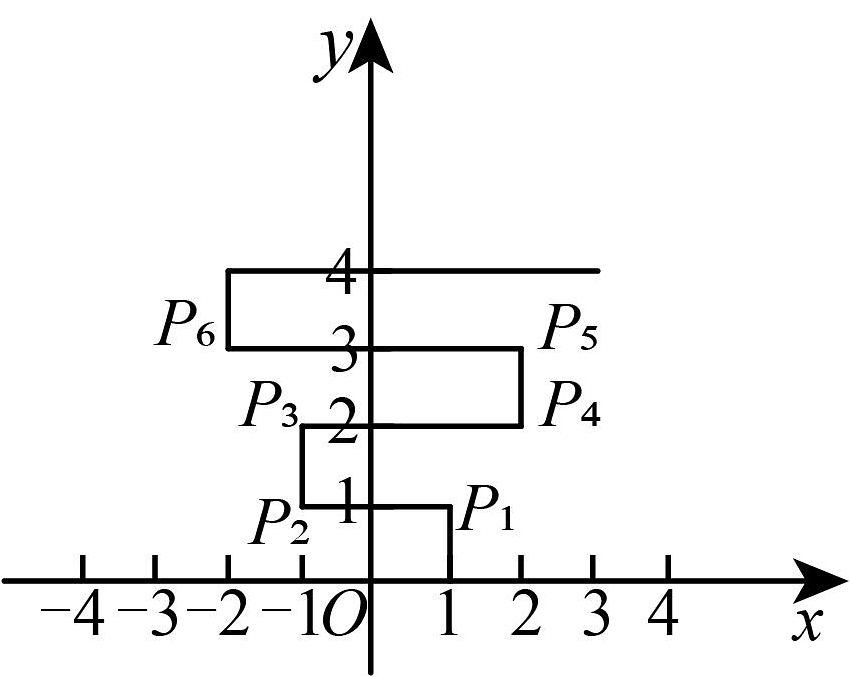 A、 B、 C、 D、
A、 B、 C、 D、 -
5、直线可以看成直线向_____平移______个单位得到的.( )A、上,1 B、下,3 C、上,4 D、下,4
-
6、已知点和关于y轴对称,则的值为( )A、0 B、 C、1 D、
-
7、如图,点是平面坐标系中一点,则点到原点的距离是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、若点在轴上,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
9、△ABC在平面直角坐标系中的位置如图所示. A、B、C三点在格点上.
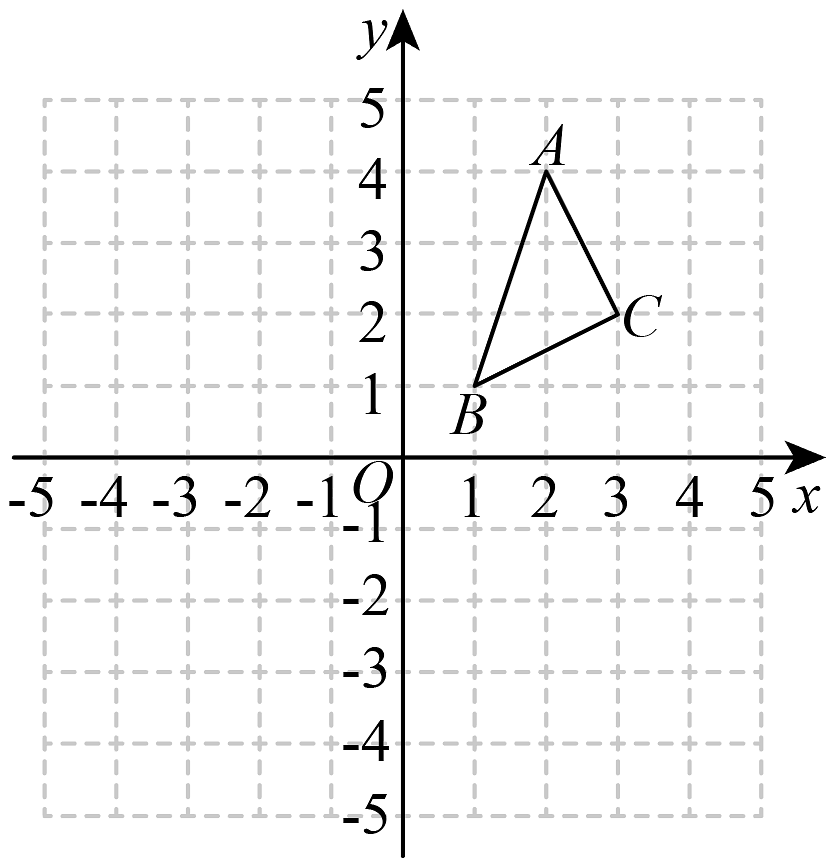
(1)作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标;
(2)作出△ABC关于y对称的△A2B2C2 , 并写出点C2的坐标.
-
10、【阅读材料】:如图(1),有A型、B型、C型三种不同的纸板,其中A型是边长为m的正方形,B型是长为m、宽为n的长方形,C型是边长为n的正方形.由图(2)中四块纸板拼成的正方形的面积关系可以说明成立.

【解决问题】:如图,有A型、B型、C型三种不同的纸板,其中A型:边长为a厘米的正方形;B型:长为a厘米,宽为1厘米的长方形;C型:边长为1厘米的正方形.
①A型2块,B型4块,C型4块.此时纸板的总面积为________平方厘米;
②从这10块纸板中拿掉1块A型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形.这个大正方形的边长为________厘米;
③从这10块纸板中拿掉2块同类型的纸板,使得剩下的纸板在不重叠的情况下,可以紧密的排出两个相同形状的大正方形,请问拿掉的是2块哪种类型的纸板?此时大正方形的面积是多少平方厘米?(计算说明)

-
11、画出数轴,并在数轴上画出表示下列各数的点,并按从小到大的顺序排列用“”号连接起来:
, , , 0, ,

-
12、已知 , 则代数式的值为 .
-
13、A、B两地相距 , 用科学记数法表示为 .
-
14、下列各式中,运算正确的是( )A、 B、 C、 D、
-
15、如图,在中, , , 是边上的中线,的垂直平分线交于点E,交于点F, .
 (1)、求证:;(2)、试判断的形状,并说明理由.
(1)、求证:;(2)、试判断的形状,并说明理由. -
16、如图,三个顶点的坐标分别为、、
 (1)、若与关于轴成轴对称,作出;并计算的面积.(2)、若P为y轴上一点,使得最小,在图中作出点P,并写出P点的坐标为______.
(1)、若与关于轴成轴对称,作出;并计算的面积.(2)、若P为y轴上一点,使得最小,在图中作出点P,并写出P点的坐标为______. -
17、计算:(1)、;(2)、
-
18、如图,在中,和的角平分线与相交于点O,过点O作 , 与分别相交于点M,N,若 , , 则的周长是 .

-
19、计算 .
-
20、如图,是的中线,是的中线,若的面积为 , 则的面积为( )
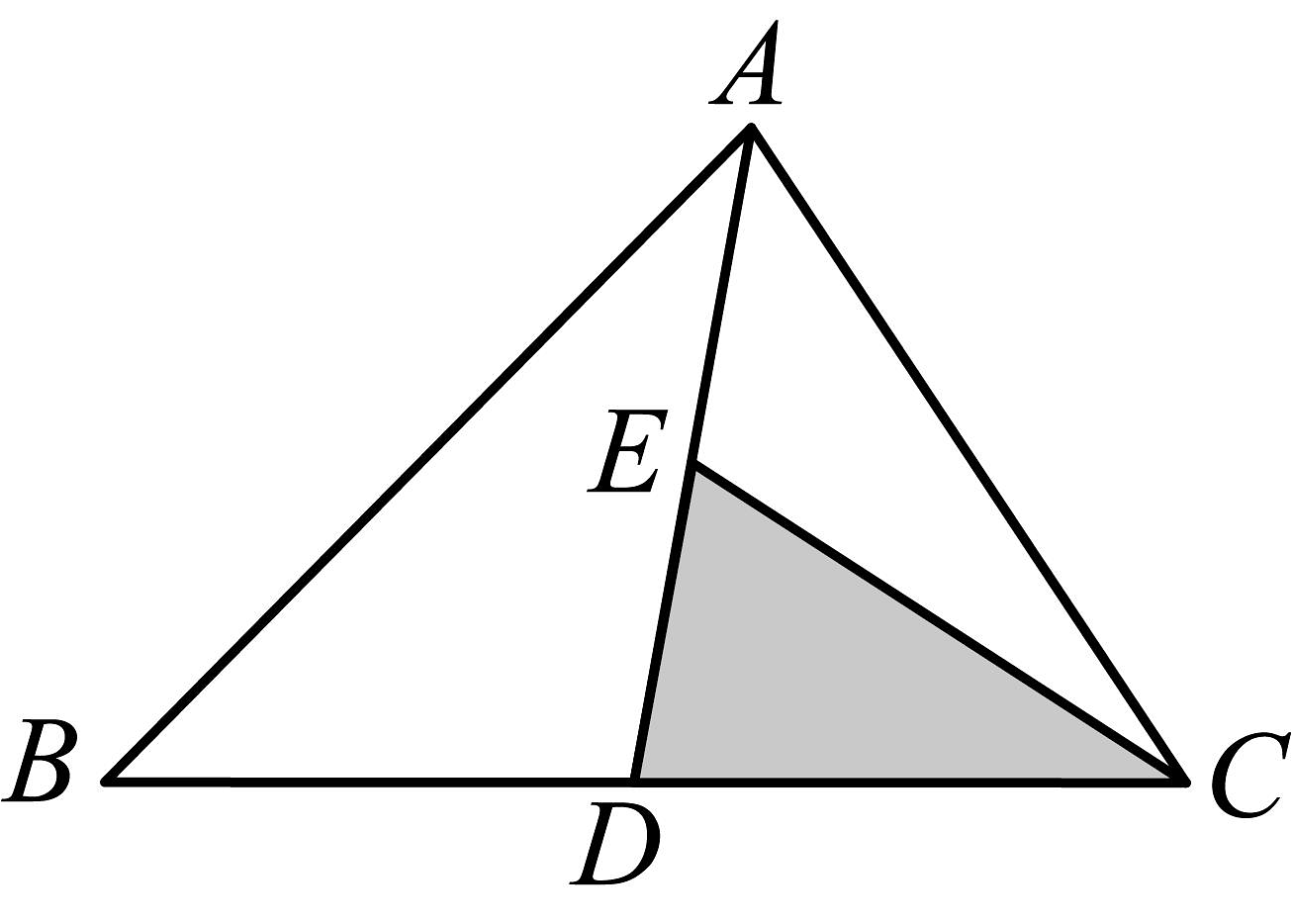 A、 B、 C、 D、
A、 B、 C、 D、