相关试卷

1、为执行国家药品降价政策，给人民群众带来实惠，某药品经过两次降价，每盒零售价由48元降为27元，设平均每次降价的百分率是x，则可列方程为（）

A、 $48 {(1 - x)}^{2} = 27$ B、 $48 {(1 + x)}^{2} = 27$ C、 $48 (1 + 2 x) = 27$ D、 $48 (1 - 2 x) = 27$

查看解析
2、如图，矩形 $O A B C$ 的顶点A，C分别在y轴和x轴上，点B的坐标为 $(2 ， 4)$ ，将矩形 $O A B C$ 绕点O逆时针旋转 $90 °$ ，得到矩形 $O A^{'} B^{'} C^{'}$ ，则点 $B^{'}$ 的坐标为（）

A、 $(- 4, - 2)$ B、 $(- 4, 2)$ C、 $(2, 4)$ D、 $(4, 2)$

查看解析
3、若 $x_{1}$ ， $x_{2}$ 是方程 $5 x^{2} + x - 5 = 0$ 的两个根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值为（）

A、 $- 1$ B、 $- \frac{1}{5}$ C、5 D、 $\frac{1}{5}$

查看解析
4、如图， $A B$ 是 $⊙ O$ 的直径， $∠ B O D = 110 °$ ，则 $∠ A E D =$ （）

A、 $28 °$ B、 $30 °$ C、 $35 °$ D、 $40 °$

查看解析
5、将抛物线 $y = x^{2}$ 向下平移3个单位长度，再向右平移5个单位长度，所得到的抛物线为（）．

A、 $y = {(x - 3)}^{2} + 5$ B、 $y = {(x - 5)}^{2} + 3$ C、 $y = {(x + 3)}^{2} - 5$ D、 $y = {(x - 5)}^{2} - 3$

查看解析
6、用配方法解一元二次方程 $x^{2} - 6 x + 4 = 0$ ，此方程可化为（）

A、 ${(x + 3)}^{2} = 1$ B、 ${(x - 3)}^{2} = 13$ C、 ${(x + 3)}^{2} = 9$ D、 ${(x - 3)}^{2} = 5$

查看解析
7、将一元二次方程 $3 x^{2} + 1 = 6 x$ 化成一般形式后，二次项系数为正，则一次项系数是（）

A、1 B、6 C、 $- 6$ D、 $- 1$

查看解析
8、定义：把在数轴上表示数 $a$ 的点与原点的距离叫做数 $a$ 的绝对值，记作 $|a|$ ．可以理解为 $|a - 0| = |a|$ ．
【运用】
（1）若 $|a| = 3$ ，则 $a =$ _____；
【拓展】根据 $|a|$ 的几何意义，式子 $|a - 2|$ 的几何意义可以理解为在数轴上表示数 $a$ 的点与2所对应的点之间的距离；式子 $|a + 1| = |a - (- 1)|$ ，所以 $|a + 1|$ 的几何意义就是在数轴上表示数 $a$ 的点与 $- 1$ 所对应的点之间的距离．
（2）式子 $|a + 5|$ 的几何意义为_____；
（3）求 $|a - 3| + |a + 5|$ 的最小值．

查看解析
9、【阅读材料】
当有理数x不等于0时，
把2个相同的有理数x的除法运算记作 $f (2, x) = x \div x$ ；
把3个相同的有理数x的除法运算记作 $f (3, x) = x \div x \div x$ ；
把4个相同的有理数x的除法运算记作 $f (4, x) = x \div x \div x \div x$ ；
…．
特别地，规定 $f (1, x) = x$ ．
【解决问题】

(1)、若 $f (n, - 2) = (- 2) \div (- 2) \div (- 2)$ ，则 $n =$ ______；

(2)、计算： $f (5, \frac{1}{4})$ ；

(3)、计算： $f (2, \frac{1}{3}) \div f (3, - 3) \times f (4, \frac{1}{2}) \times f (1, - 1)$ ．

查看解析
10、阅读例题的计算方法．
例：计算： $- 5 \frac{5}{6} + (- 9 \frac{2}{3}) + 17 \frac{3}{4} + (- 3 \frac{1}{2})$ ．
解：原式 $= [(- 5) + (- \frac{5}{6})] + [(- 9) + (- \frac{2}{3})] + (17 + \frac{3}{4}) + [(- 3) + (- \frac{1}{2})]$
$= [(- 5) + (- 9) + 17 + (- 3)] + [(- \frac{5}{6}) + (- \frac{2}{3}) + \frac{3}{4} + (- \frac{1}{2})]$
$= 0 + (- 1 \frac{1}{4})$
$= - 1 \frac{1}{4}$ ．
上面这种解题方法叫做拆项法．

(1)、计算： $(- 16 \frac{11}{17}) + (+ 14 \frac{3}{7}) + (+ 12 \frac{11}{17}) + (- 15 \frac{3}{7})$ ；

(2)、计算： $(+ 2024 \frac{4}{5}) + (- 1890 \frac{5}{9}) + (+ 1008 \frac{3}{5}) + (- 1142 \frac{4}{9})$ ．

查看解析
11、如图，长为 $60 cm$ ，宽为 $x cm$ 的大长方形被分割成7小块，除阴影部分A，B外，是形状、大小完全相同的小长方形，其较短一边长为 $y cm$ ．

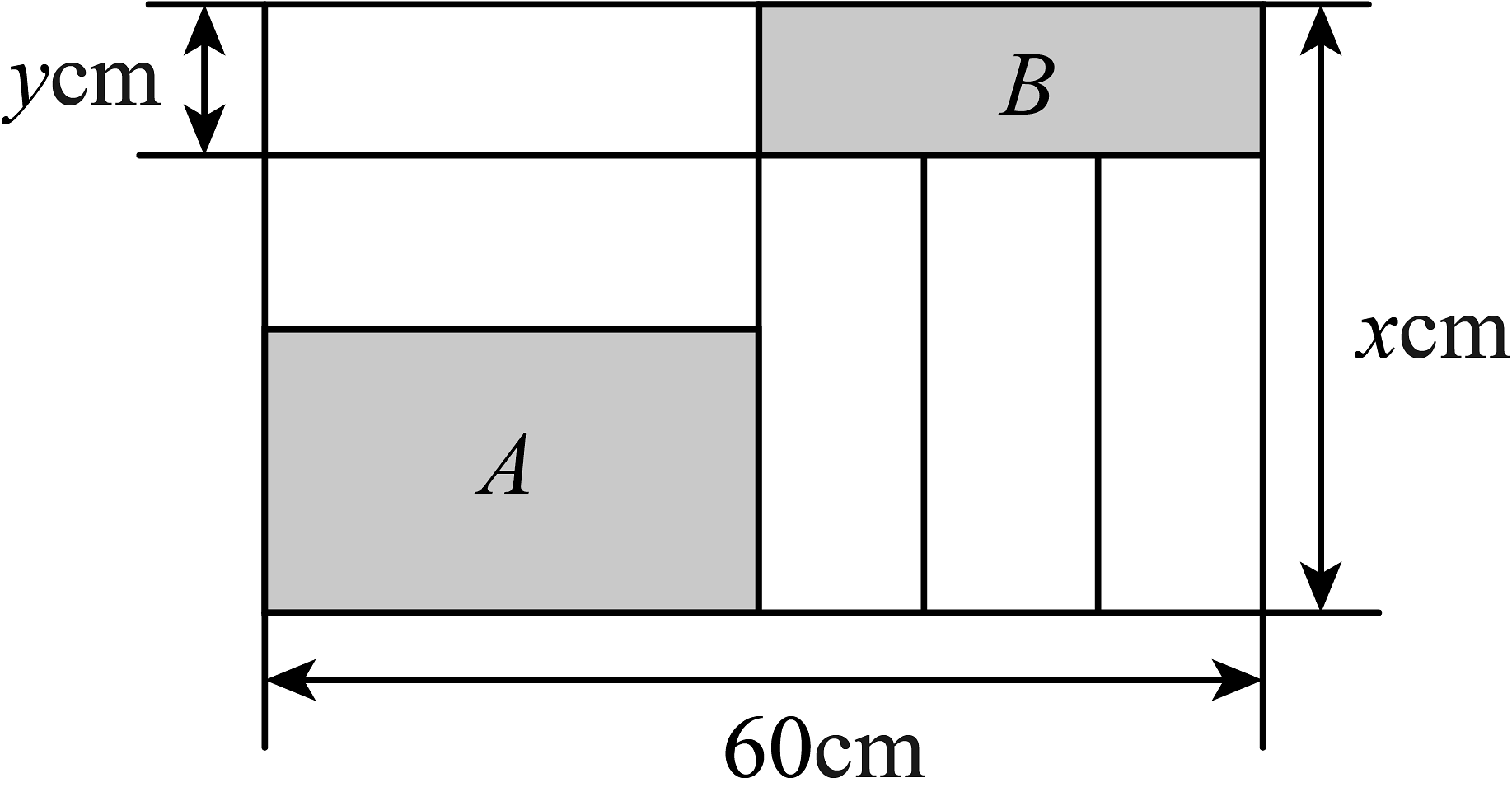(1)、由图可知，这5块完全相同的小长方形较长边的长是______ $cm$ ；（用含y的代数式表示）

(2)、当 $x = 40, y = 10$ 时，分别计算阴影部分A，B的面积．

查看解析
12、下列图形都是由同样大小的⊙按一定规律所组成的，其中第1个图形中一共有4个⊙，第2个图形中一共有7个⊙，第3个图形中一共有10个⊙，⋯，按此规律排列．

(1)、第5个图形中一共有_______个⊙；

(2)、第100个图形中一共有_______个⊙；

(3)、想一想：第n个图形中一共有多少个⊙？（用含n的代数式表示）

查看解析
13、若定义一种新的运算“*”，规定有理数 $a * b = 4 a b$ ，如 $2 * 3 = 4 \times 2 \times 3 = 24$ ．

(1)、求 $5 * (- 3)$ 的值；

(2)、求 $(- \frac{1}{6}) * (\frac{3}{2} * 5)$ 的值．

查看解析
14、在国庆节的七天长假中，某风景区10月1日的旅游人数为6万人，后面的六天与10月1日相比每天旅游人数变化如下表：（正数表示人数增加）
日期
2日
3日
4日
5日
6日
7日
人数变化（单位：万人）
$+ 0.6$
$- 0.4$
$- 0.3$
$+ 0.3$
$+ 0.1$
$+ 0.1$

(1)、七天长假中游客人数最多的一天比最少的一天多几万人？

(2)、据测算，平均每位游客为风景区带来的旅游收入约为200元，则该风景区在这七天假期的旅游总收入约为多少元？（结果用科学记数法表示）

查看解析
15、先化简，再求值： $2 (3 a^{2} b - a b^{2}) - 3 (- a b^{2} + 2 a^{2} b)$ ，其中 $a = 2, b = - 3$ ．

查看解析
16、计算： ${(- 3)}^{2} - {(1 \frac{1}{2})}^{2} \times \frac{4}{9} - 16 \div |- \frac{2}{3}|$ ．

查看解析
17、已知 $|x| = 3$ ， $|y| = 5$ ．
（1）若x，y异号，则 $x y$ 的值是；
（2）若 $x + y < 0$ ，则 $x - y$ 的值是．

查看解析
18、比 $- 2024$ 大2025的数是．

查看解析
19、比较大小： $|- 2024|$ 2023．（填“ $<$ ”“ $=$ ”或“ $>$ ”）

查看解析
20、如图是一个数据运算程序，如果开始输入的x的值为10，那么第1次输出的结果是5，返回进行第二次运算，则第2次输出的结果是16，…，以此类推，第2024次输出的结果是（）

A、2 B、4 C、8 D、1

查看解析

上一页 1069 1070 1071 1072 1073 下一页跳转

日期	2日	3日	4日	5日	6日	7日
人数变化（单位：万人）	$+ 0.6$	$- 0.4$	$- 0.3$	$+ 0.3$	$+ 0.1$	$+ 0.1$