-
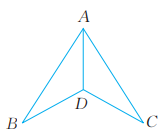
1、 已知:如图,AD平分. 求证:
-
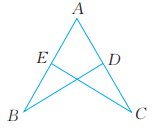
2、 已知:如图,点D,E分别在AC,AB上, 求证:AE=AD。
-
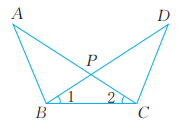
3、已知:如图,AC与DB相交于点P,∠1=∠2,∠ABC=∠DCB。求证:AP=DP,BP=CP。
-
4、已知:如图,在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B',BC=B'C'。求证:△ABC≌△A'B'C'。

-
5、一块三角形玻璃被摔成三片(如图)。如果只带上其中的一片,玻璃店的师傅就能重新配一块与原来相同的三角形玻璃,那么你知道应带哪一片碎玻璃吗?请说明理由。

-
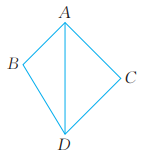
6、 如图,已知四边形ABDC的面积为14,AD平分∠BAC,AB+AC=7。求点D到AB的距离。
-
7、已知△ABC(如图),在△ABC所在的平面内,用直尺和圆规求作一点D,使点D到AB,AC的距离相等,且DC=DB。

-
8、 如图,在△ABC中,∠C=90°,AD平分∠CAB,BD=2CD。若点D到AB的距离DE为5.6cm,求BC的长。

-
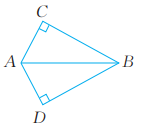
9、 已知:如图,AB平分∠CAD,∠C=∠D=90°。求证:BC=BD。
-
10、如图,已知△ABC,用直尺和圆规分别作出∠A和∠C的平分线。

-
11、用直尺和圆规过已知直线上一点作已知直线的垂线。
-
12、证明:三角形的两条角平分线的交点到各边的距离相等。
-
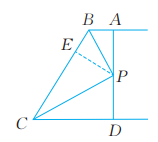
13、已知:如图,AB∥CD,PB,PC分别平分∠ABC,∠DCB,AD过点P,且与AB垂直。求证:PA=PD。
-
14、任意作一个角,记为∠BAC,P是∠BAC的平分线上的一点,PB⊥AB于点B,PC⊥AC于点C。比较PB和PC的大小,并证明你的结论。

-
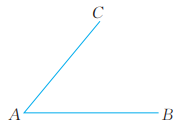
15、已知∠BAC(图),用直尺和圆规作 的平分线AD。
-
16、从报刊、图书、网络等搜集一些能用一元一次不等式解决的问题,分析其中的数量关系,建立不等式模型加以解决。
-
17、两根木棒的长分别是5cm和7cm。要选择第三根木棒,将它们首尾相接钉成一个三角形。若第三根木棒的长为偶数,则第三根木棒长的取值情况有几种?
-
18、小聪用100元钱购买笔记本和黑色中性笔共30件。已知每本笔记本5元,每支黑色中性笔2元。问:小聪最多能买多少本笔记本?
-
19、 已知-1<a<2,-2<b<-1,求a+2b和a-2b的取值范围。
-
20、求满足不等式组 的x的整数值。