-
1、 已知：如图，在△ABC中，D是AB上一点，∠1=∠B，∠A=∠2。求证：△ABC是直角三角形。
-
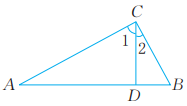
2、在如图的方格纸上画三个互不全等的直角三角形，使其顶点都在格点上，并用符号“Rt△”和字母将它们表示出来。
-
3、已知：如图，在△ABC中，CD是AB边上的中线，
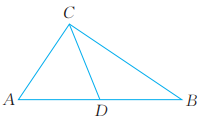
求证：△ABC是直角三角形。
-
4、根据下列条件判断△ABC是不是直角三角形，并说明理由。(1)、 有一个外角为90°；(2)、 ∠A=36°，∠B=54°；(3)、 如图，∠1与∠2互余，∠B=∠1。
-
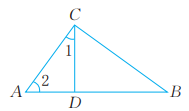
5、 已知：如图，AB=AD，AC=AE，∠BAC=∠DAE=90°。求证：
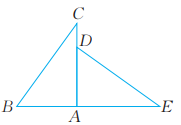(1)、∠C=∠E。(2)、 ED⊥BC。 -
6、 已知：如图，AB∥DE，AB=DE，点B，E，C，F在一条直线上，且BE=CF。求证：AC∥DF。
-
7、 已知：如图，AC=BD，∠CAB=∠DBA。求证：
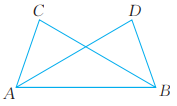(1)、 △ABC≌△BAD。(2)、 BC=AD，∠C=∠D。 -
8、已知：如图， 。求证：
-
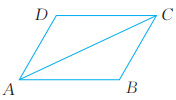
9、如图，已知线段a，c和 ， 用直尺和圆规作 使
-
10、(1)、设计实验来探究。如图，木条AB，AC的长度确定，均可绕点A转动。若 的大小确定，则 的形状、大小唯一确定吗?
(2)、用尺规作图来验证你的猜想。 -
11、为了测量池塘两端A，B间的距离，小红在地面上选择了点O，D，C，使 且点A，O，C和点B，O，D分别都在一条直线上。 小红认为只要量出点D，C间的距离，就能知道点A，B间的距离。你认为正确吗?请说明理由。
-
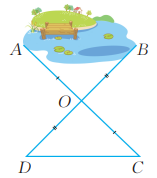
12、 已知：如图，AB=AC，点D，E分别在AC，AB上，且AD=AE。
求证：BD=CE(填空)。
证明：在和 ▲ 中，
因为 ，
所以 ▲ ≌ ▲ ( )，
所以BD=CE ( ) 。
-
13、已知：如图，AB=DB，BC=BE，∠1=∠2。求证：∠C=∠E。
-
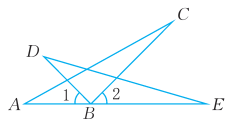
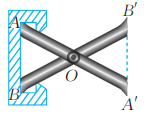
14、如图，把两根钢条AA'，BB'的中点钉在一起，可以做成一个测量工件内槽宽的卡钳。说明卡钳的工作原理。
-
15、已知：如图，AC与BD相交于点O，且OA=OC，OB=OD。
求证：△AOB≌△COD。
-
16、已知：如图，AB∥CD，∠A=∠C。求证：AD=BC。
-
17、阅读下面一段文字：
泰勒斯(Thales，约前624~前547)是古希腊哲学家。相传“两个角及其夹边对应相等的两个三角形全等”就是由泰勒斯首先提出的。泰勒斯利用这个判定三角形全等的依据求出了岸上一点到海中一艘船的距离。
如图，A是观测点，船P在A的正前方。过A作AP的垂线l，在垂线l上截取任意长AB，O是AB的中点。观测者从点B沿垂直于AB的BK方向走，直到点K和船P、点O在一条直线上，那么BK的长度即为船离岸的距离。
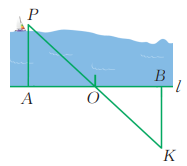
请给出证明。
-
18、已知：如图， 。求证： .
-
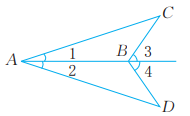
19、根据所给条件，下列各题中的两个三角形一定全等吗?若不一定，请举出反例；若一定，说明理由。(1)、 △ABC和△MNP中，∠A=∠M，AB=MN；(2)、△RST和△XYZ中，∠R=∠X，∠S=∠Y，∠T=∠Z。
-
20、如图，在. 和 中，点B，E，C，F在同一条直线上。下面给出四个论断：
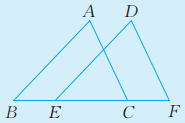
①； ②
③∠ABC=∠DEF； ④BE=CF。
任选三个作为已知条件，余下一个作为结论，可得到几个命题?其中真命题有几个?分别给出证明。