-
1、(1)实验操作:如图1,将两个含角的全等的三角尺摆放在一起,你能通过实验操作,借助这个图形,找到的直角边与斜边之间的数量关系.
教材中有这样的结论:在直角三角形中,如果一个锐角等于 , 那么它所对的直角边等于斜边的一半.请结合图2,写出已知,求证,并证明该结论;
(2)实践思考:如图3,四边形是一张长方形纸片,将纸片折叠,使点A与点D,点B与点C重合,得到折痕后再把纸片展平;在上选一点P,沿折叠 , 使点D恰好落在折痕上的点M处.求证: .
(3)拓展运用:如图4,已知三角形衣架中, , , 求的面积.

-
2、在中, , 为边中点,点在 , 所在直线上, .
 (1)、若 , 如图1,画点 , 使点与点关于所在直线对称,连 , , 直接写出的大小;(2)、如图2,点在延长线上,点在延长线上,点为点关于所在直线的对称点,连 , 求证: .
(1)、若 , 如图1,画点 , 使点与点关于所在直线对称,连 , , 直接写出的大小;(2)、如图2,点在延长线上,点在延长线上,点为点关于所在直线的对称点,连 , 求证: . -
3、由小正方形组成的3×6网格,每个小正方形的顶点叫做格点.的三个顶点均是格点,仅用无刻度的直尺在给定网格中完成画图.
 (1)、请在图①中完成画图:先在上画点D,连 , 使于点D,再画的高;(2)、请在图②中完成画图:先在上画点F,连 , 使刚好平分的面积,再在上画点G,连 , 使 .
(1)、请在图①中完成画图:先在上画点D,连 , 使于点D,再画的高;(2)、请在图②中完成画图:先在上画点F,连 , 使刚好平分的面积,再在上画点G,连 , 使 . -
4、一个等腰三角形的一边长为 , 周长为 , 求其他两边的长.
-
5、如图,D是的边上一点,点E是中点,连DE并延长至点F,使 .
 (1)、求证:;(2)、添加一个条件,使 , 请直接写出这个条件(不用说明理由).
(1)、求证:;(2)、添加一个条件,使 , 请直接写出这个条件(不用说明理由). -
6、如图,线段 , 交于点O,连 , , , . 求证: .

-
7、如图,点D为的边延长线上一点, , 若 , , 则的度数为 .

-
8、如图,在中,有如下操作:

(1)分别以点B,C为圆心,大于的长为半径画弧,分别交于点M,N;
(2)直线交 , 于点D,E;
(3)以点A为圆心,任意长为半径画弧交 , 于点G,H;
(4)分别以点G,H为圆心,大于的长为半径画弧,在的内部交于点P;
(5)射线交直线于点Q,交于点F.现有以下结论:
①若 , , 则;
②点D为中点;
③若 , , 则的面积是的面积的2倍;
④若 , , , 的面积为 , 则的长为1.
其中正确的结论序号是 .
-
9、如图1, , 如图2, , 如图3, . 依此类推:的度数和是°.

-
10、如图, , 为方格纸中格点上的两点,若以为边,在方格中取一点(在格点上),使得为等腰三角形,则点的个数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、马小虎在计算凸多边形内角和时,把其中一个内角多加了一次,得到内角和为 , 则这个多边形的边数是( ).A、4 B、5 C、6 D、7
-
12、过边形的一个顶点可以画条对角线,将它分成个三角形,则的值是( )A、 B、 C、 D、
-
13、一个凸多边形的每个内角均为 , 则这个多边形对角线的条数是( ).A、1条 B、2条 C、3条 D、4条
-
14、等腰三角形的一边长为4,一边长为9,则它的周长是( ).A、17 B、22 C、17或22 D、1
-
15、如图,在人字梯的中间一般会设计一拉杆,这样做的原理是( )
 A、两点之间,线段最短 B、三角形的稳定性 C、两点确定一条直线 D、两直线平行,同位角相等
A、两点之间,线段最短 B、三角形的稳定性 C、两点确定一条直线 D、两直线平行,同位角相等 -
16、已知三角形的两边分别为和 , 则第三边可能是( ).A、 B、 C、 D、
-
17、观察下列方程及解的特征: ⑴x+=2的解为x1=x2=1;
⑵x+=的解为x1=2,x2=;
⑶x+=的解为x1=3,x2=;
解答下列问题:
(1)请猜想:方程x+=的解为________;
(2)请猜想:关于x的方程x+═________ 的解为x1=a,x2=(a≠0);
(3)下面以解方程x+=为例,验证(1)中猜想结论的正确性.
-
18、如图,M是的半径的中点,弦于点M,过点C作交的延长线于点D,连接 .

(1)求的值;
(2)求证:是的切线.
-
19、把两个大小相同的含角的三角尺如图放置,若 , 求三角尺各边的长.
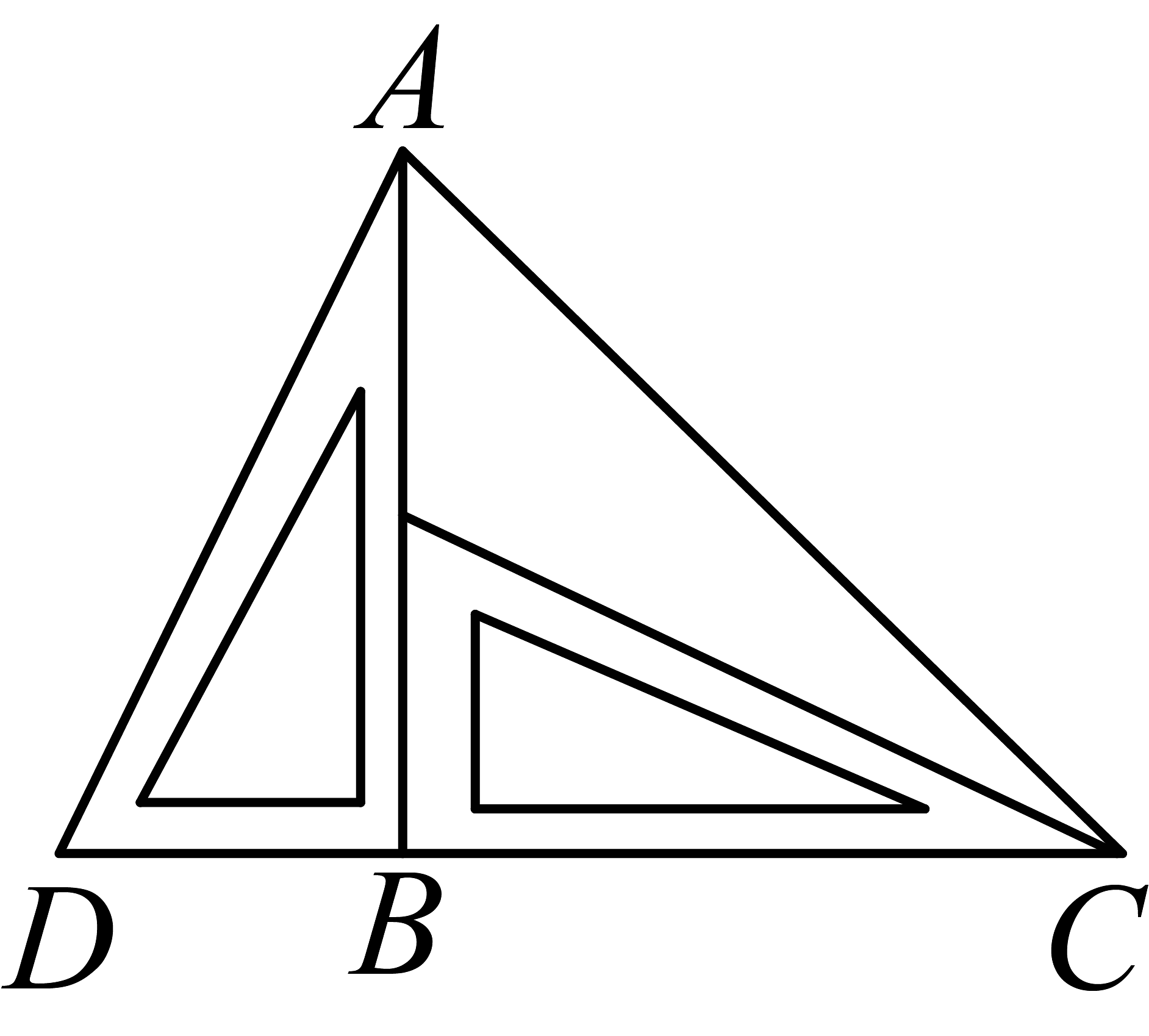
-
20、中, .(1)、如果 , , 求的长;(2)、如果 , , 求的长.