相关试卷

1、小明从家里出发骑车去舅舅家做客，他骑了一段时间后，想起要买个礼物送给表弟，于是又折回到刚经过的一家商店，买好礼物后继续骑车去舅舅家，如图是小明离家的距离与随时间变化而变化的情况．观察图象并回答下列问题：

(1)、请直接写小明家到舅舅家路程是多少米？小明在商店停留了几分钟？

(2)、在去舅舅家的行程中，求小明一共骑行了多少米？一共用了多少分钟？

(3)、在去舅舅家的途中哪个时间段小明骑车速度最快？最快的速度是多少米 $/$ 分？（请说明理由）

查看解析
2、如图所示方格纸中，每个小正方形的边长均为1，点 $A$ ，点 $B$ ，点 $C$ 在小正方形的顶点上．

(1)、画出 $△ A B C$ 中边 $B C$ 上的高 $A D$ ；

(2)、画出 $△ A B C$ 中边 $A C$ 上的中线 $B E$ ；

(3)、直接写出 $△ A B C$ 的面积为________．

查看解析
3、 $△ A B C$ 在平面直角坐标系中的位置如图所示．将 $△ A B C$ 向右平移5个单位长度，再向下平移4个单位长度得到 $△ A_{1} B_{1} C_{1}$ ， $△ A B C$ 内部有一点 $D (m, n)$ 平移后的对应点为 $D_{1}$ ．（图中每个小方格边长均为1个单位长度）．

(1)、在图中画出平移后的 $△ A_{1} B_{1} C_{1}$ ；

(2)、直接写出下列各点的坐标： $C_{1}$ ______， $D_{1}$ ______；

查看解析
4、如图，在平面直角坐标系中，直线 $y = k x + b$ 和 $y = m x + n$ 相交于点（2，－1），则关于 $x$ 、 $y$ 的方程组 $\{\begin{matrix} k x = y - b \\ m x + n = y \end{matrix}$ 的解为．

查看解析
5、不等式 $- 3 \leq 2 x + 3 \leq 7$ 的解集是．

查看解析
6、已知a、b、c分别是 $△ A B C$ 的三边长，a、b满足 $|a - 7| + {(b - 1)}^{2} = 0$ ， c为奇数，则 $△ A B C$ 的周长为．

查看解析
7、甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离A城的距离 $y (km)$ 与甲车行驶的时间 $t (h)$ 之间的函数关系如图所示．下列结论：①A，B两城相距 $300 km$ ；②乙车比甲车晚出发 $1 h$ ，却早到 $1 h$ ；③甲车的速度为 $60 km/h$ ；④乙车的速度为 $80 km/h$ ．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看解析
8、棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图是局象棋残局，若在中国象棋盘上建立平面直角坐标系，使表示棋子“馬”和“車”的点的坐标分别为（4，3），（﹣2，1），则表示“炮”的点的坐标为（　　）

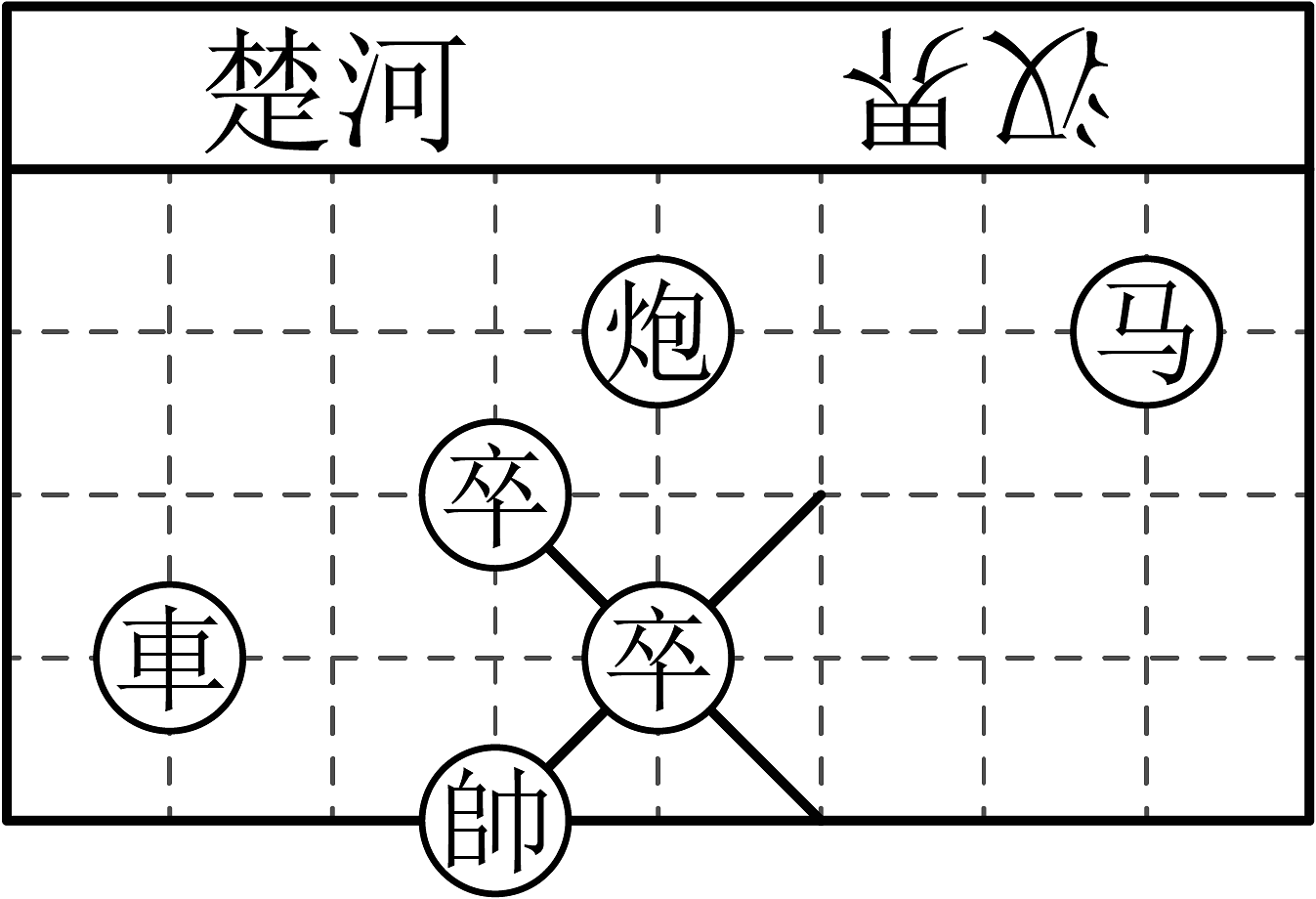A、（1，3） B、（3，1） C、（2，3） D、（1，2）

查看解析
9、函数 $y = \frac{1}{x + 1}$ 中自变量 $x$ 的取值范围是（）

A、 $x < 0$ B、 $x \leq - 1$ C、 $x > - 1$ D、 $x \neq - 1$

查看解析
10、点P在第二象限内，且P到x轴的距离是4，到y轴的距离是3，那么点P的坐标为（）

A、 $(- 4, 3)$ B、 $(4, - 3)$ C、 $(- 3, 4)$ D、 $(3, - 4)$

查看解析
11、在平面直角坐标系中，下列各点位于第四象限的是（）

A、 $(- 2, 1)$ B、 $(- 1, - 2)$ C、 $(1, 2)$ D、 $(1, - 2)$

查看解析
12、【问题背景】
我们知道 $| x |$ 的几何意义是：在数轴上数 $x$ 对应的点与原点 $O$ 的距离，这个结论可以推广为： $|x_{1} - x_{2}|$ 表示在数轴上数 $x_{1}$ ， $x_{2}$ 对应点之间的距离．
【问题解决】
（1）在数轴上， $A$ 点表示的数是 $2$ ， $B$ 点表示的数是 $- 3$ ，则点 $A$ 与点 $B$ 之间的距离 $A B =$ ______．
（2）如果点 $A$ 在数轴上表示的数为 $x$ ，点 $B$ 在数轴上表示的数为 $- 4$ ，点 $A$ 与点 $B$ 之间的距离 $A B$ 为5，那么 $x =$ ______．
（3）若 $| - 1 - x | + |2 - x| = 3$ ，且 $x$ 为整数，则 $x$ 的值为______．
【关联运用】
如图，点 $A$ 、 $B$ 、 $C$ 是数轴上的三点， $A$ 点表示数是 $- 2$ ， $B$ 点表示数是1， $C$ 点表示数是7．点 $A$ ， $B$ ， $C$ 开始在数轴上运动，若点 $A$ 以每秒1个单位长度的速度向左运动，同时，点 $B$ 和点 $C$ 分别以每秒2个单位长度和4个单位长度的速度向右运动，假设 $t$ 秒钟过后，求点 $A$ 与点 $B$ 之间的距离，点 $B$ 与点 $C$ 之间的距离．（用含 $t$ 的代数式表示）．

查看解析
13、理解与思考：整体代换是数学的一种思想方法．例如：若 $x^{2} + x = 0$ ，则 $x^{2} + x + 1186 =$ ______；我们将 $x^{2} + x$ 作为一个整体代入．则原式 $= 0 + 1186 = 1186$ ．仿照这样的解题方法，完成下面的问题：

(1)、若 $x^{2} + x - 1 = 0$ ，则 $x^{2} + x + 2024 =$ ______；

(2)、若 $a + b = 3$ ，求 $2 (a + b) - a - b + 21$ 的值：

(3)、若 $a^{2} + 2 a b = 20$ ， $b^{2} + 2 a b = 8$ ，则 $a^{2} + b^{2} + 4 a b =$ ______．

(4)、当 $x = 1$ 时，代数式 $a x^{5} + b x^{3} + c x - 5$ 的值为 $m$ ，求当 $x = - 1$ 时，代数式 $a x^{5} + b x^{3} + c x - 5$ 的值．

查看解析
14、已知关于 $x$ 的多项式 $A$ ， $B$ ．其中 $A = m x^{2} + 2 x - 1$ ， $B = x^{2} - n x + 2$ （ $m$ ， $n$ 为有理数），若 $2 B - A$ 的结果不含 $x$ 项和 $x^{2}$ 项，求 $m - n$ 的值．

查看解析
15、（1）化简： $2 (a b^{2} - 2 a^{2} b) - 3 (a b^{2} - a^{2} b) + (2 a b^{2} - 2 a^{2} b)$
（2）已知： $A = 4 x^{2} - 4 x y + y^{2}$ ， $B = x^{2} + x y - 5 y^{2}$ ，求 $A - 2 B$ 的值．

查看解析
16、观察下列各式：
$\frac{1}{2} \times \frac{2}{3} = \frac{1}{3}$
$\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} = \frac{1}{4}$
$\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} \times \frac{4}{5} = \frac{1}{5}$
…
将一根长2025厘米的绳子先截去它的 $\frac{1}{2}$ ，再截去余下的 $\frac{1}{3}$ ，再截去余下的 $\frac{1}{4}$ ，再截去余下的 $\frac{1}{5}$ ，以此类推，直到最后截去余下的 $\frac{1}{2025}$ ，最后还剩是厘米．

查看解析
17、如图，某同学设计了一种计算程序流程图，当输入的 $x$ 的值为 $- 3$ 时，输出的 $y$ 的值为．

查看解析
18、某商品原价是每件 $a$ 元，第一次降价打九折，第二次降价再打八折，则第二次降价后的售价为每件元．（用含 $a$ 的式子表示）

查看解析
19、有理数 $a$ ， $b$ 在数轴上的位置如图所示，化简 $| b - a | - | a + b |$ 的结果为．

查看解析
20、若关于 $x$ 的整式 $(m + 3) x^{m} + x^{2}$ 是三次二项式，则 $m =$ ．

查看解析

上一页 1025 1026 1027 1028 1029 下一页跳转