-
1、若 , 且 , 则( )A、5或7 B、或 C、或5 D、或7
-
2、数轴上点P表示的数为 , 与点距离为4个单位长度的点表示的数为( )A、1 B、 C、1或 D、1或
-
3、某面粉厂加工的面粉袋上,标有标准质量为的字样,从中产品中任意拿出一袋称重,质量不符合标准重量的要求的是( ).A、 B、 C、 D、
-
4、若 , 则的值是( )A、 B、4 C、0 D、1
-
5、下列说法错误的是( )A、是一次三项式 B、是二次三项式 C、是五次二项式 D、是二次二项式
-
6、如图,这个方格中每个方格都表示一个数,且每相邻三个数之积为 , 则表示的数是( )A、 B、 C、 D、
-
7、在等边三角形的两边所在直线上分别有两点M、N,P为外一点,且 , , . 探究:当点M、N分别在直线移动时,之间的数量关系.
 (1)、如图①,当点M、N在边上,且时,的数量关系是.(2)、如图②,当点M、N在边上,且时,上述结论还成立吗?试说明理由.(3)、如图③,当点M、N分别在边的延长线上时,请直接写出之间的数量关系.
(1)、如图①,当点M、N在边上,且时,的数量关系是.(2)、如图②,当点M、N在边上,且时,上述结论还成立吗?试说明理由.(3)、如图③,当点M、N分别在边的延长线上时,请直接写出之间的数量关系. -
8、在平面直角坐标系中,将一个直角的顶点放在点处,直角的两边分别交两坐标轴正半轴于A、B两点,
 (1)、求证:;(2)、求四边形的面积;
(1)、求证:;(2)、求四边形的面积; -
9、如图,已知△ABC的顶点分别为A(-2,2)、B(-4,5)、C(-5,1)和直线m(直线m上各点的横坐标都为1).
(1)作出△ABC关于x轴对称的图形 , 并写出点的坐标;
(2)作出点C关于直线m对称的点 , 并写出点的坐标;
(3)在x轴上画出点P,使PA+PC最小.

-
10、如图,已知和均是等边三角形,点在同一条直线上,与相交于点 , 与交于点 , 与相交于点 , 连接 , 则下列结论:①;②;③;④;⑤;其中正确结论的序号是 .

-
11、如图,两根竹竿AB和BD斜拿在墙上,量得 , 的度数分别为38°,26°,则的度数为 .

-
12、如图,四边形ABCD中,∠BAD=121°,∠B=∠D=90°,在BC、CD上分别找到一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
 A、118° B、121° C、120° D、119°
A、118° B、121° C、120° D、119° -
13、如图,中,分别平分和 , 过点作交于点 , 交于点 , 那么下列结论:
①;②为等腰三角形;③的周长等于的周长;④ . 其中正确的是( )
 A、①② B、①③ C、①②④ D、①②③④
A、①② B、①③ C、①②④ D、①②③④ -
14、如图,已知 , , 是正边形的三条边,在同一平面内,以为边在该正边形的外部作正方形 . 若 , 则的值为( )
 A、12 B、10 C、8 D、6
A、12 B、10 C、8 D、6 -
15、杭州亚运会,作为亚洲体育盛事的一次精彩呈现,不仅展示了各国运动员的卓越才能,也彰显了杭州这座城市的独特魅力.下列关于体育运动的图标中,是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、
-
16、如图1, , 为中点,点在上方,连接 , .
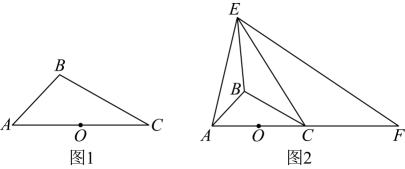 (1)、尺规作图:作点关于点的对称点(保留作图痕迹,不写作法),连接 , , 并证明:四边形为平行四边形;(2)、如图2,延长至点 , 使得 , 当点在直线的上方运动,直线的上方有异于点的动点 , 连接 , , , , 若 , 且 .
(1)、尺规作图:作点关于点的对称点(保留作图痕迹,不写作法),连接 , , 并证明:四边形为平行四边形;(2)、如图2,延长至点 , 使得 , 当点在直线的上方运动,直线的上方有异于点的动点 , 连接 , , , , 若 , 且 .①求证:;
②的长是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
-
17、某玩转数学小组发现隧道前通常设有涉水线和限高架等安全警示,为探究其内在的数学原理,该小组考察了如图1所示的双向通行隧道.以下为该小组研究报告的部分记录,请认真阅读,解决问题.

发现问题确定目标
涉水线设置
限高架设置
数学抽象绘制图形
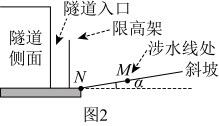
隧道及斜坡的侧面示意图,可近似如图2所示.
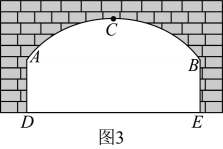
图3为隧道横截面示意图,由抛物线的一部分和矩形的三边构成.
信息收集资料整理
当隧道内积水的水深为0.27米时,(即积水达到涉水线处),车辆应避免通行.
车辆进入隧道,应在行驶车道内通行(禁止压线),且必须保证车辆顶部与隧道顶部在竖直方向的空隙不小于0.3米.
实地考察数据采集
斜坡的坡角为 , 并查得: ,
,
.
隧道的最高点C到地面距离为5.4米,两侧墙面高米,地面跨度米.车辆行驶方向的右侧车道线(宽度忽略不计)与墙面的距离为1米.
问题解决:
(1)、如图2,求涉水线离坡底的距离(精确到0.01米);(2)、在图3中建立适当的平面直角坐标系,求抛物线的解析式;(3)、限高架上标有警示语“车辆限高h米”(即最大安全限高),求h的值(精确到米). -
18、宽与长的比是(约为)的矩形叫做黄金矩形.现有一张黄金矩形纸片 , 长 . 如图1,折叠纸片 , 点B落在上的点E处,折痕为 , 连接 , 然后将纸片展开.
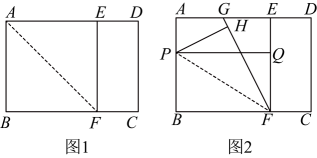 (1)、求的长;(2)、求证:四边形是黄金矩形;(3)、如图2,点G为的中点,连接 , 折叠纸片 , 点B落在上的点H处,折痕为 , 过点P作于点Q . 四边形是否为黄金矩形?如果是,请证明:如果不是,请说明理由.
(1)、求的长;(2)、求证:四边形是黄金矩形;(3)、如图2,点G为的中点,连接 , 折叠纸片 , 点B落在上的点H处,折痕为 , 过点P作于点Q . 四边形是否为黄金矩形?如果是,请证明:如果不是,请说明理由. -
19、智能机器人广泛应用于智慧农业.为了降低成本和提高采摘效率,某果园引进一台智能采摘机器人进行某种水果采摘.(1)、若用人工采摘的成本为a元,相比人工采摘,用智能机器人采摘的成本可降低 . 求用智能机器人采换的成本是多少元;(用含a的代数式表示)(2)、若要采摘4000千克该种水果,用这台智能采摘机器人采摘比4个工人同时采摘所需的天数还少1天,已知这台智能采摘机器人采摘的效率是一个工人的5倍,求这台智能采摘机器人每天可采摘该种水果多少千克.
-
20、如图,曲线过点 .
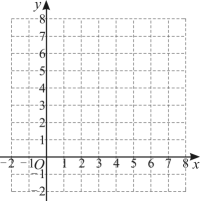 (1)、求t的值;(2)、直线也经过点P , 求l与y轴交点的坐标,并在图中画出直线l;(3)、在(2)的条件下,若在l与两坐标轴围成的三角形内部(不包含边界)随机取一个格点(横、纵坐标都是整数的点),求该格点在曲线G上的概率.
(1)、求t的值;(2)、直线也经过点P , 求l与y轴交点的坐标,并在图中画出直线l;(3)、在(2)的条件下,若在l与两坐标轴围成的三角形内部(不包含边界)随机取一个格点(横、纵坐标都是整数的点),求该格点在曲线G上的概率.