-
1、如图,在和中, , , .
 (1)、求证: .(2)、若 , 求的度数.
(1)、求证: .(2)、若 , 求的度数. -
2、阅读材料:求的值.
解:设①,将等式①的两边同乘以2,
得②,
用得, ,
即 ,
即 .
请仿照此法计算:
(1)、请直接填写的值为______;(2)、求值;(3)、请直接写出的值. -
3、电动车厂某周5天(周六、周日休息)计划生产辆电动车,平均每天生产电动车辆,由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
星期
一
二
三
四
五
减增
(1)、该厂星期一生产电动车______辆;(2)、生产量最多的一天比生产量最少的一天多生产电动车______辆;(3)、该厂实行计件工资制,每生产一辆电动车可得元,那么该厂工人这周的工资总额是多少元? -
4、用四舍五入法将精确到百分位,所得到的近似数为 .
-
5、如图,线段 , 点C在线段上,点N在线段上,且 , M是线段的中点.
 (1)、求线段的长度;(2)、若 , 求线段的长度.
(1)、求线段的长度;(2)、若 , 求线段的长度. -
6、如图,直线AD、BC交于点O, , 若 , , , 则的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、胶票每天的涨、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.已知一只股票某天跌停,之后两天时间又涨回到原价.若这两天此股票股价的平均增长率为x,则x满足的方程是( )A、 B、 C、 D、
-
8、大自然是美的设计师,一个盆景也会产生最具美感的黄金分割比.如图,点B为的黄金分割点 , 则( )
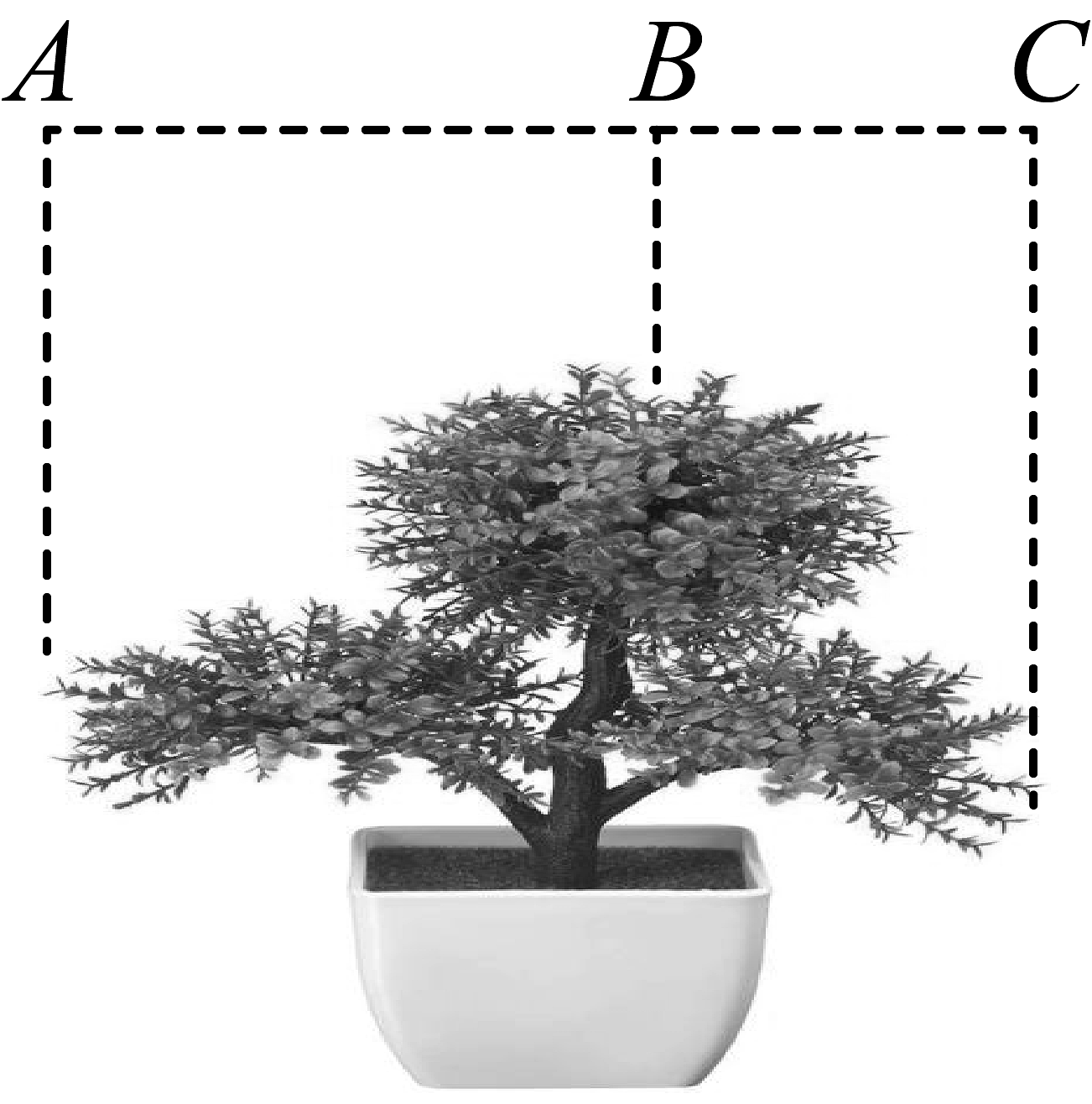 A、 B、 C、 D、
A、 B、 C、 D、 -
9、如图1,这是一个3阶魔方,由三层完全相同的小立方体组成,体积为27.
 (1)、求出这个魔方的棱长.(2)、图中阴影部分是一个正方形 , 求出阴影部分的面积及其边长.(3)、在图2的方格中画一个面积为10的正方形;并将数轴补充完整,然后用圆规在数轴上表示实数 .
(1)、求出这个魔方的棱长.(2)、图中阴影部分是一个正方形 , 求出阴影部分的面积及其边长.(3)、在图2的方格中画一个面积为10的正方形;并将数轴补充完整,然后用圆规在数轴上表示实数 . -
10、某校在2021年组织七年级学生参加研学活动,租用二种不同型号的客车,每辆座位如下表:
客车型号
A
B
人数/辆
28
49
若租用 A型客车5辆和 B型客车2辆,则需要租金2500元;若租用 A型客车1辆和 B型客车5辆,则需要租金 2800 元.
(1)、求租用A,B两种型号客车,每辆车租金分别是多少元?(2)、现有七年级14个班级的学生588人,现计划同时租用两种型号客车,一次送完,且恰好每辆车都坐满,为节约成本,则租用 A型客车和 B型客车各多少辆,需要花费多少钱? -
11、随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场,一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲,乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
A种水果/箱
B种水果/箱
甲店
11元
17元
乙店
9元
13元
有两种配货方案(整箱配货):
方案一:甲,乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店几箱,乙店几箱?B种水果甲店几箱,乙店几箱?
(1)、如果按照方案一配货,请你计算出经销商能盈利多少元;(2)、请你将方案二补充完整,写出所有结果,并将你填写的方案二与方案一做比较,得出哪一种方案盈利较多. -
12、4的平方根是 , 算术平方根是 .
-
13、如图所示,下列语句描述正确的是( )
①若∠1=∠3,则AB∥DC;②若∠C+∠1+∠4=180°,则AD∥BC;③∠A=∠C,∠ABC=∠ADC,则AB∥DC;④若∠2=∠4,BD平分∠ABC,则BC=CD;⑤若AD∥BC,∠A=∠C,则AB∥DC.
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、五月份学校将举办“雅信杯”校园好声音大赛,某班进行了预选赛,为鼓励同学们,老师花了48元钱买了甲、乙两种(两种都买)励志标语牌作为奖品.已知甲种励志标语牌每个6元,乙种励志标语牌每个4元,则老师购买励志标语牌的方案共有( )A、1种 B、2种 C、3种 D、4种
-
15、如图,已知直线AB与CD平行,直线EF与AB,CD分别交于点E,F,若∠1=125°,则∠2=( )
 A、65° B、55° C、50° D、45°
A、65° B、55° C、50° D、45° -
16、若与是同位角,且 , 则是( )A、 B、 C、或 D、不能确定
-
17、某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知 , , , 则的度数是( )
 A、38° B、44° C、46° D、56°
A、38° B、44° C、46° D、56° -
18、在生活中,密码的应用随处可见,密码学是一门既古老又新兴的学科,它主要研究如何安全地传递和存储保密信息.如图,现制定一种密码规则,这种规则在正整数和字母、字符之间建立了一种对应关系,其中正整数为密文,字母、字符为明文.例如,密文“2”翻译成明文为“C”,密文“258”翻译成明文为“CZ”.
 (1)、明文“A”对应的密文为“_______”(写出符合条件的一种情况即可),密文“483847”翻译成明文为“_______”;(2)、为了增加密码的破译难度,对于密文按如下规则又进行了再次加密,原密文记为“密文I”,再次加密的密文记为“密文Ⅱ”.
(1)、明文“A”对应的密文为“_______”(写出符合条件的一种情况即可),密文“483847”翻译成明文为“_______”;(2)、为了增加密码的破译难度,对于密文按如下规则又进行了再次加密,原密文记为“密文I”,再次加密的密文记为“密文Ⅱ”.密文I:
1
2
3
4
…
密文Ⅱ:
7
10
13
16
…
①若密文I中的正整数每增加1,则密文Ⅱ中正整数的变化规律为_______;
②若密文I中的“t”对应的明文与密文Ⅱ中的“3t+4”直接利用原规则对应的明文相同,求该明文.
-
19、如图,已知 , 轴于点B,且满足 .
 (1)、求A点坐标;(2)、分别以 , 为边作等边和等边 , 如图1,试判断线段和的数量关系,并说明理由;(3)、如图2,若P为y轴上异于原点O和点B的一个动点,连接 , 过P点作 , 且 , 连接 , 射线交延长线于Q,当P点在y轴上移动时,线段的值是否发生变化.若不变化,直接写出长度的值;若变化,请说明理由.
(1)、求A点坐标;(2)、分别以 , 为边作等边和等边 , 如图1,试判断线段和的数量关系,并说明理由;(3)、如图2,若P为y轴上异于原点O和点B的一个动点,连接 , 过P点作 , 且 , 连接 , 射线交延长线于Q,当P点在y轴上移动时,线段的值是否发生变化.若不变化,直接写出长度的值;若变化,请说明理由. -
20、解分式方程:(1)、;(2)、 .