-
1、尺规作图:在矩形中,要求用直尺和圆规作菱形 , 使点分别在边上.

小明:如图1,作的中垂线分别交于点 , 连结 .
小刚:如图2,连结 , 作的中垂线分别交于点 , 连结 .
请选择一位同学的作法,判断是否正确,并说明理由.(注:若全选,按第一种作答评分)
-
2、某校举行班容班貌评比活动,以班级为单位,评比项目包括文化卫生、板报宣传和特色栏目.三个班级各项目得分如下表(单位:分)所示:
项目
班级
文化卫生
板报宣传
特色栏目
班
92
88
93
班
94
93
89
班
89
94
96
(1)、已知两班的平均分分别是91分、92分,通过计算指出哪个班级平均分最高.(2)、若将文化卫生、板报宣传和特色栏目的得分按的比例计算总成绩,此时班的总成绩分别为分和分,求班的总成绩,并根据总成绩从高到低给出班级排名. -
3、如图,为四边形的对角线,已知 .
 (1)、求证:四边形是平行四边形.(2)、分别为的中点,连结 . 若 , 求的长.
(1)、求证:四边形是平行四边形.(2)、分别为的中点,连结 . 若 , 求的长. -
4、(1)计算: .
(2)解方程: .
-
5、如图,矩形的顶点在轴正半轴上,A为的中点,反比例函数(为常数,)的图象经过点 , 交于点 . 若与的面积之和为4,则的值为 .

-
6、每年4月23日是世界读书日,某校为了解学生周末课外阅读情况,随机抽取了30名学生,得到统计图如图所示,则该30名学生周末课外阅读时间的众数为小时.
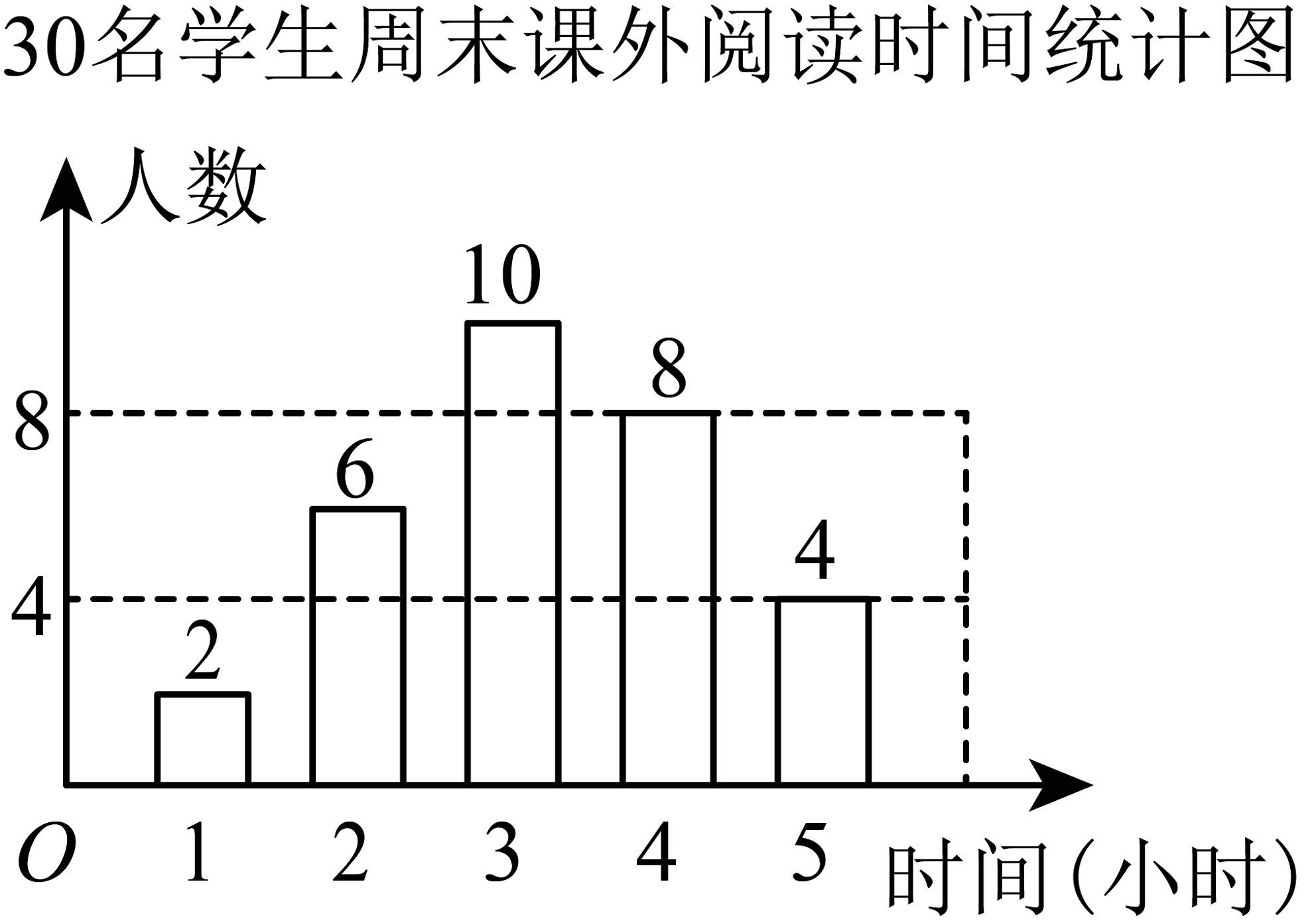
-
7、小马同学在解方程时,等号左边的一个数字不小心被墨水污染了,如右式:
 . 已知一个根 , 则另一个根 .
. 已知一个根 , 则另一个根 . -
8、计算: .
-
9、如图,点在线段上,射线 , 连结 , 以为邻边作 , 连结 , 记的长为的长为 . 若 , , , 则在点的运动过程中,下列代数式的值不变的是( )
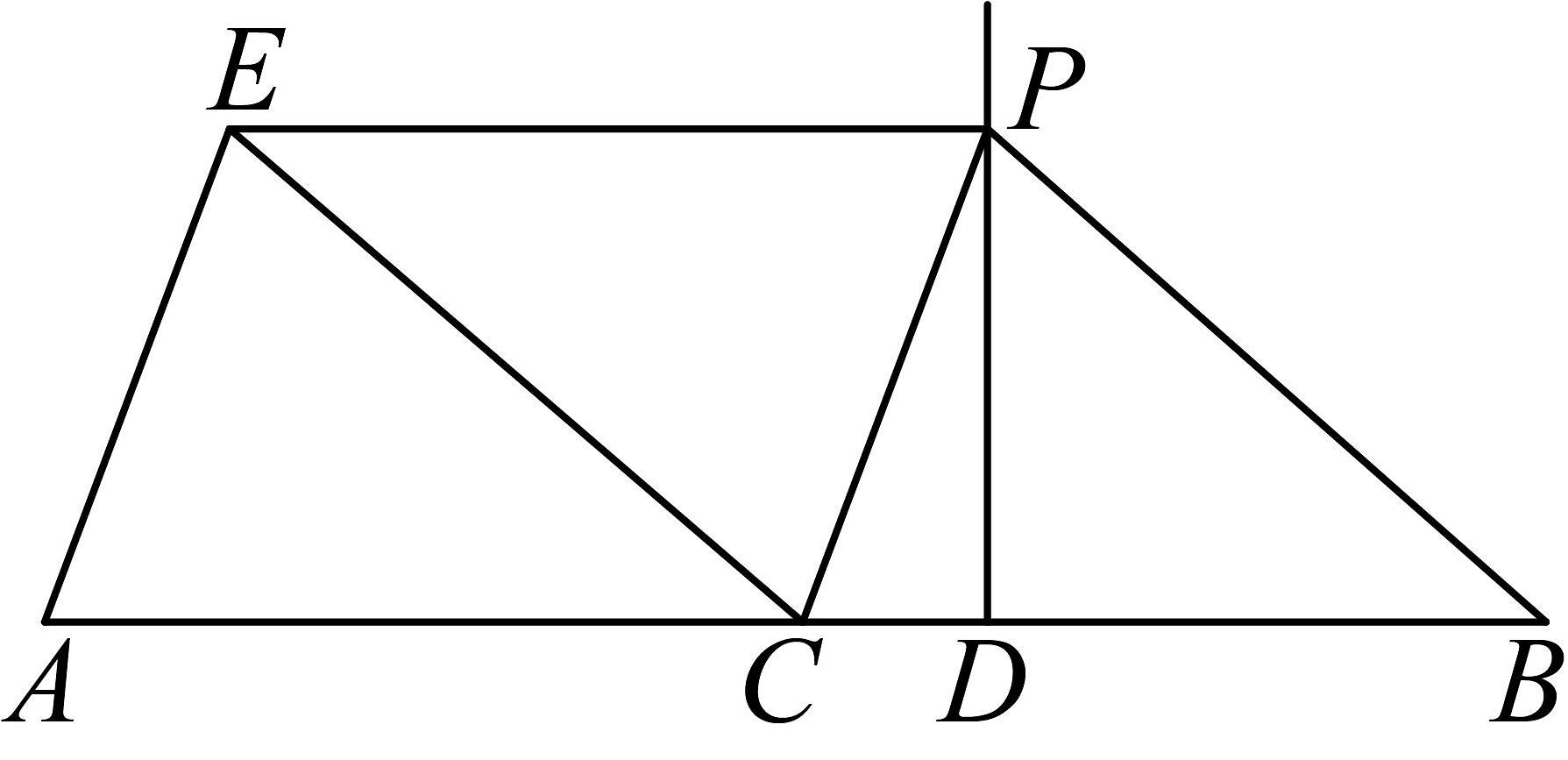 A、 B、 C、 D、
A、 B、 C、 D、 -
10、王老师设计了接力游戏:每人只能看到前一人的方程,并继续进行变形,将结果传递给下一人,最终求出方程的解,过程如图所示.
上述求解过程中,错误的是( )
A、甲 B、乙 C、丙 D、丁 -
11、温州市2022年(国内生产总值)约为8030亿元,2024年约为9719亿元.设这两年温州市的平均增长率为 , 则可列出方程( )A、 B、 C、 D、
-
12、若算式的结果是有理数,则※表示的运算符号是( )A、 B、 C、 D、
-
13、若点都在反比例函数的图象上,则下列判断正确的是( )A、 B、 C、 D、
-
14、用反证法证明命题“在中,如果 , 那么”时,应假设( )A、 B、 C、 D、
-
15、如图,在菱形中,交于点 . 若 , 则的长为( )
 A、5 B、6 C、8 D、10
A、5 B、6 C、8 D、10 -
16、下列四个人工智能的图标中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
17、小明作业本中有一页被墨水污染了,已知他所列的方程组是正确的,写出题中被墨水污染的条件,并求解这道应用题.
应用题:小东在某商场中看中的一台电视和一台空调在“五一”前共需要5500元.由于该商场开展“五一”促销活动,同样的电视打八折销售,
 ,于是小东在促销期间购买了同样的电视一台.空调两台,共花费7200元.求“五一”前同样的电视和空调每台各多少元?
,于是小东在促销期间购买了同样的电视一台.空调两台,共花费7200元.求“五一”前同样的电视和空调每台各多少元?解:设“五一”前同样的电视每台x元,空调每台y元,根据题意,得

-
18、如图,直线与直线相交于点 , 与轴分别交于两点.
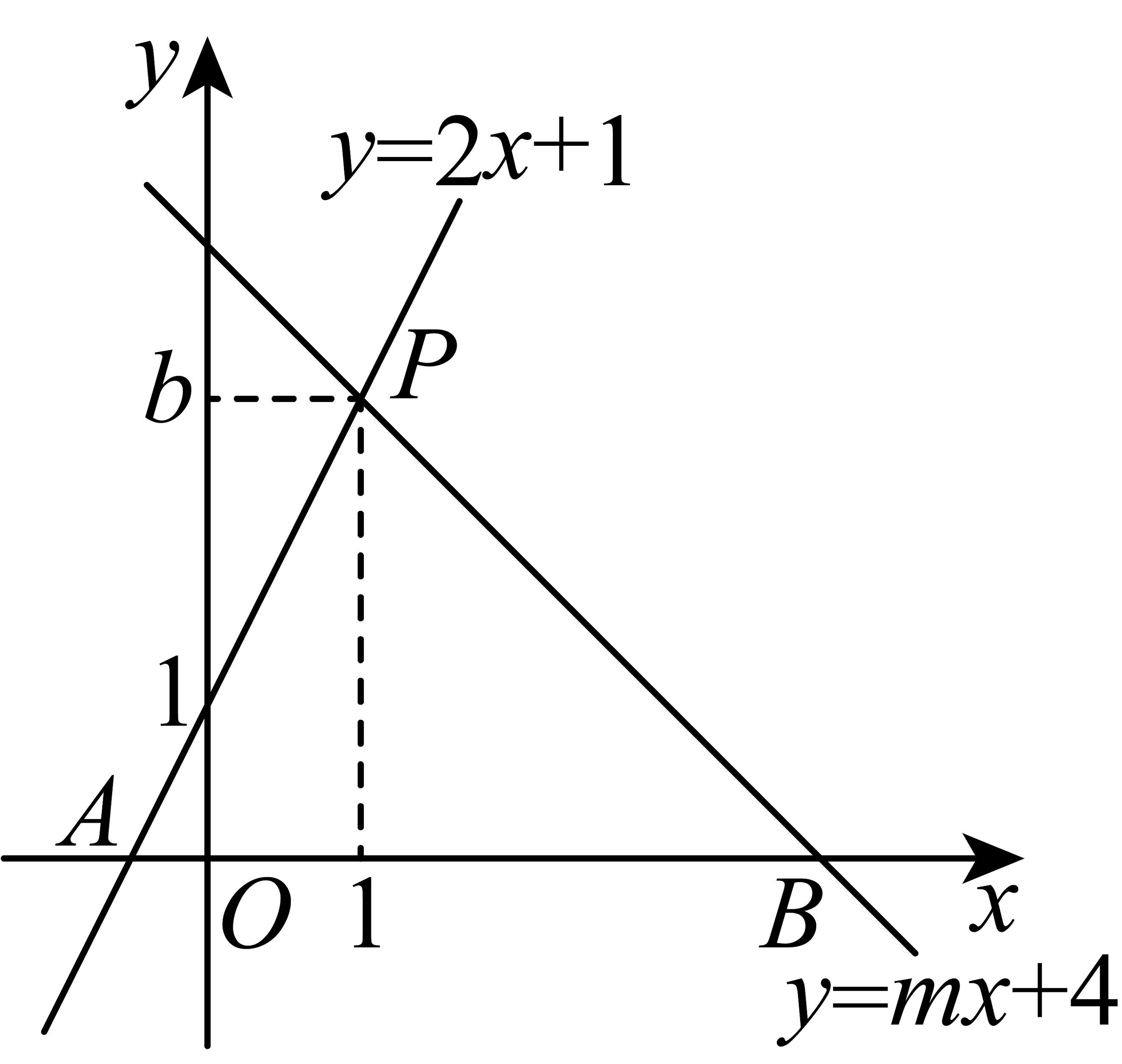 (1)、求的值,并结合图象写出关于的方程组的解;(2)、根据图象,直接写出关于的不等式的解集;(3)、求的面积.
(1)、求的值,并结合图象写出关于的方程组的解;(2)、根据图象,直接写出关于的不等式的解集;(3)、求的面积. -
19、【项目背景】《中华人民共和国保守国家秘密法》是规范围家秘密保护的基础性法律,首次颁布于年,历经了年和年两次重大修订,最新修订版本于年月日起实施,今年月日是该部法律实施一周年纪念日,某校为了解同学们对该部法律的了解情况,选取了部分同学进行调查.
【数据的收集与整理】
该校道德与法治老师从七、八年级中各随机抽取了相同人数的学生进行答卷测评将抽查学生的成绩进行如下分组:
组别
并将抽查学生的成绩制成如下的统计图表:
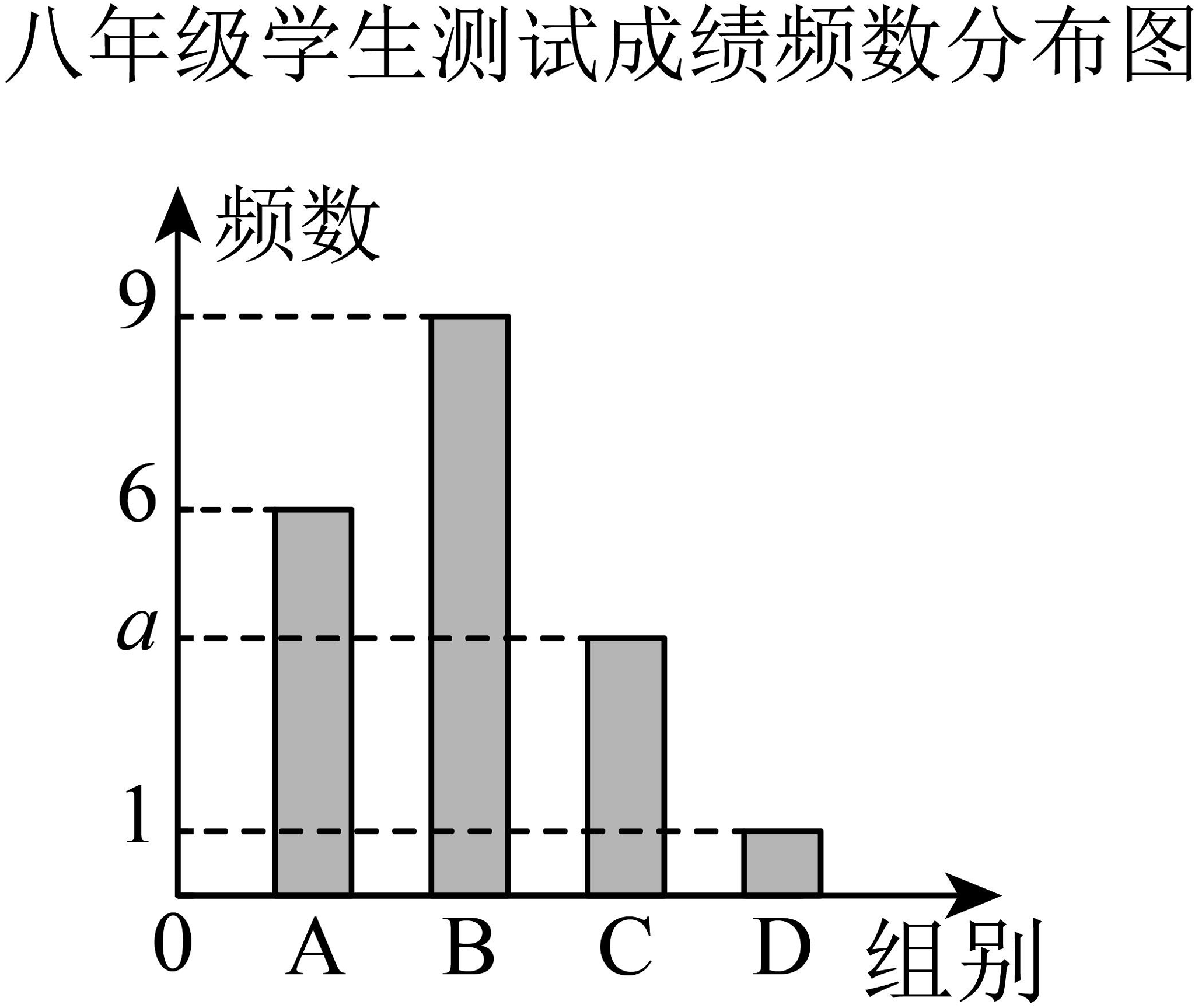
八年级学生测试成绩频数分布表
组别
频数
频率
—
七年级组学生成绩(单位:分)为 .
【数据分析与应用】
任务:本次抽查的七、八年级学生共多少人?的值是多少?
任务:该校七年级共人,请估计七年级全体学生对法律了解情况是组别的学生数量;
任务:从七年级组学生中选取名男生和名女生,从八年级组学生中选取名男生和名女生组成《中华人民共和国保守国家秘密法》宣讲团,某天该校从宣讲团中任选一名同学到六年级宣讲该法律,求抽到的同学是女生的概率.
-
20、如图,已知锐角 , . 请用尺规作图法,在内部求作一点P,使 , 且 (保留作图痕迹,不写做法).