安徽省合肥市庐江县2015-2016学年八年级上学期数学期末考试试卷
试卷更新日期：2018-02-26 类型：期末考试
一、单选题
-
1. PM2.5是指大气中直径小于或等于0.000 002 5米的颗粒物，将0.000 002 5用科学记数法表示为（ ）A、0.25×10﹣5 B、2.5×10﹣5 C、2.5×10﹣6 D、2.5×10﹣72. 下列汽车标志图案中，不是轴对称图形的是（ ）A、
B、
C、
D、
3. 下列运算中，正确的是（ ）A、4a•3a=12a B、a•a2=a3 C、（3a2）3=9a6 D、（ab2）2=ab44. 如图，AB∥CD，AD和BC相交于点O，∠A=20°，∠COD=100°，则∠C的度数是（ ）
A、80° B、70° C、60° D、50°5. 与分式 的值相等的分式是（ ）A、 B、 C、 D、﹣6. 一个多边形的内角和是外角和的2倍，则这个多边形的边数为（ ）A、4 B、5 C、6 D、77. 如果9x2+kx+25是一个完全平方式，那么k的值是（ ）A、15 B、±5 C、30 D、±308. 等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的底边为（ ）A、3cm B、7cm C、7cm或3cm D、8cm9. 若P=（a+b）2 ， Q=4ab，则（ ）A、P＞Q B、P＜Q C、P≥Q D、P≤Q10. 如图，已知：∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A5B5A6的边长为（ ）
A、6 B、16 C、32 D、64二、填空题
-
11. 因式分解a3﹣4a的结果是 ．12. 已知点A（1﹣a，5）与点B（3，b）关于y轴对称，则a﹣b的值是 ．
13. 请写出同时满足以下两个特点的一个分式：①分式有意义时字母的取值范围是x≠1；②当x=2时，分式的值为3，这样的分式可以是 ．
14. 如图，C为线段AE上一点（不与点A、E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，以下四个结论：①△ACD≌△BCE；②△CDP≌△CEQ；③PQ∥AE；④∠AOB=60°．一定成立的结论有（把你认为正确结论的序号都填上）．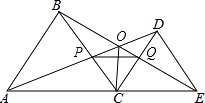
三、解答题
-
15. 先化简（ ﹣ ）÷ ，然后从﹣1、﹣ 、1中选取一个你认为合适的数作为a的值代入求值．
16. 画出△ABC关于y轴对称的图形△A1B1C1；在x轴上找出点P，使得点P到点A、点B的距离之和最短（保留作图痕迹）
17. 阅读下面求y2+4y+8的最小值的解答过程．解：y2+4y+8=y2+4y+4+4=（y+2）2+4
∵（y+2）2≥0
∴（y+2）2+4≥4
∴y2+4y+8的最小值为4．
仿照上面的解答过程，求x2﹣2x+3的最小值．
18. 如图，在△ABC中，AC=BC，AD平分∠BAC，∠ADC=60°，求∠C的度数．
19. 如图，在边长为（2m+3）的正方形纸片中剪出一个边长为（m+3）的正方形之后，剩余部分可剪拼成一个长方形，若拼成的长方形一边长为m，求另一边长．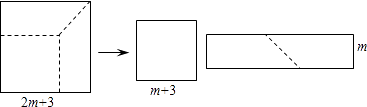
20. 如图：已知等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DM⊥BC，垂足为M，求证：M是BE的中点．
21. 根据条件，求式子的值．(1)、已知a+ =﹣3，求a2+ 的值；(2)、已知 + =2，求 的值．22. 某水果店第一次用600元购进水果若干千克，第二次又用600元购进该水果，但这次每千克的进价比第一次进价的提高了25%，购进数量比第一次少了30千克．
(1)、求第一次每千克水果的进价是多少元？
(2)、若要求这两次购进的水果按同一价格全部销售完毕后获利不低于420元，问每千克售价至少是多少元？
23. 已知等边△ABC的边长为4cm，点P，Q分别从B，C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；点Q沿CA，AB向终点B运动，速度为2cm/s，设它们运动的时间为x（s），
(1)、如图（1），当x为何值时，PQ∥AB；
(2)、如图（2），若PQ⊥AC，求x；
(3)、如图（3），当点Q在AB上运动时，PQ与△ABC的高AD交于点O，OQ与OP是否总是相等？请说明理由．