-
1、已知直线y=kx+b（k≠0）经过点A（3，0），B（1，2）。(1)、求直线y=kx+b的函数表达式。(2)、若直线y=x-2与直线y=kx+b相交于点C，求点C的坐标。(3)、写出不等式kx+b>x-2的解集。
-
2、如图，经过点B（-2，0）的直线y=kx+b与直线y=4x+2相交于点A（-1，-2），则不等式4x+2>kx+b的解集为（ ）
A、x<-2 B、x>-1 C、x<-1 D、x>-2 -
3、关于x的一次函数y=（k+2）x-2k+1，其中k为常数且k≠-2。有下列结论：①当k=0时，此函数为正比例函数；②无论k取何值，此函数图象必经过（2，5）；③若函数图象经过（m，a为常数），则；④无论k取何值，此函数图象都不可能同时经过第二、三、四象限。其中正确的有。（填序号）
-
4、若A（-1，y1）和B（m，y2）在函数y=-3x+b（b为常数）的图象上，且则m的值可能是（ ）A、-2 B、-1 C、0 D、2
-
5、已知一次函数其中a≠1。(1)、若点在y1的图象上，求a的值。(2)、当-2≤x≤3时，若函数有最大值2，求y1的函数表达式。(3)、对于一次函数其中m≠-1，若对一切实数x，都成立，求a，m需满足的数量关系及a的取值范围。
-
6、把函数y=x的图象向上平移3个单位，则下列各点中，在平移后的直线上的是（ ）A、（2，2） B、（2，3） C、（2，4） D、（2，5）
-
7、若一次函数的图象过点A（1，3），B（-1，-1），则该一次函数的表达式为。
-
8、当x=-1时，函数y=kx+3的值为5，则k的值为。
-
9、设一次函数y=kx+b（k，b为常数，k≠0）的图象过A（1，3），B（-5，-3）两点。(1)、求该函数的表达式。(2)、若点C（a+2，2a-1）在该函数图象上，求a的值。(3)、设点P在x轴上，若S△ABP=12，求点P的坐标。
-
10、函数y=3x-6，当函数值y=18时，自变量x的值是。
-
11、下列平面直角坐标系中的图象，不能表示y是x的函数的为（ ）A、
B、
C、
D、
-
12、在平面直角坐标系中，A（2，2），B（4，3），C（a，b），其中点C是由点A向左平移1个单位，再向上平移2个单位得到的。
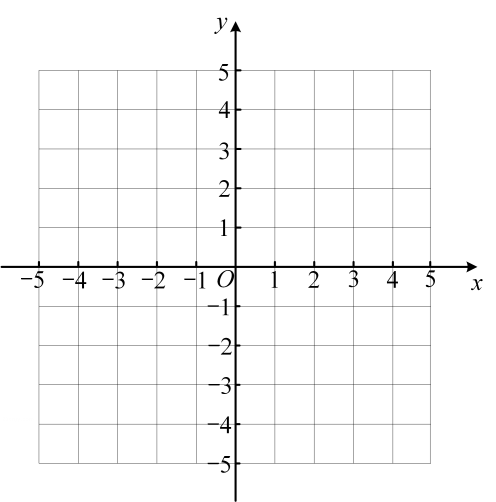(1)、求a，b的值。(2)、作出△ABC，判断它的形状并说明理由。 -
13、如图，在平面直角坐标系中，点A的坐标为作轴于点B，连结AO，将绕点B按逆时针方向旋转得到则点C的坐标为（ ）
A、 B、 C、 D、 -
14、将以A（-2，7），B（-2，2）为端点的线段AB向右平移2个单位得到线段下列各点中，在线段上的是（ ）A、（0，3） B、（-2，1） C、（0，8） D、（-2，0）
-
15、如图，在平面直角坐标系中，已知A（0，a），B（b，0），C（3，c）三点，若a，b，c满足关系式
(1)、求a，b，c的值。(2)、求四边形AOBC的面积。(3)、是否存在点使的面积为四边形AOBC的面积的两倍?若存在，请求出点P的坐标；若不存在，请说明理由。 -
16、定义：在平面直角坐标系中，把从点P出发沿横或纵方向到达点Q（至多拐一次弯）的路径长称为P，Q两点的“实际距离”。如图，若P（-1，1），Q（2，3），则P，Q两点的“实际距离”为5，即PS+SQ=5或PT+TQ=5。环保节能的公共自行车逐渐成为市民出行时喜爱的交通工具。设A，B，C三个小区的坐标分别为A（3，3），B（6，-2），C（0，-4），若点M表示公共自行车停放点，且满足点M到A，B，C的“实际距离”相等，则点M的坐标是。
-
17、在平面直角坐标系中，电子跳蚤从原点出发，按向右、向上、向左再向上的方向依次循环跳动，每次跳动1个单位，其行走路线如图所示，则点A2024的坐标是（ ）
A、（0，1011） B、（0，1013） C、（0，1012） D、（1，1012） -
18、如图，在平面直角坐标系中，已知A（-2，1），B（1，0），将线段AB绕着点B按顺时针方向旋转90°得到线段BA'，则点A'的坐标为。
-
19、在边长为1个单位的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上。（小正方形的顶点称为格点）
(1)、在平面直角坐标系中作出△ABC关于y轴对称的 ， 点与A、B1与B对应，并回答下列问题：①写出点的坐标。
②已知点P是线段上任意一点，用恰当的方式表示点P的坐标。
(2)、若△ABC平移后得到点A的对应点的坐标为（-1，-1），写出点B的对应点B2的坐标。 -
20、已知△ABC是直角坐标系中任意位置的一个三角形，现将△ABC各顶点的纵坐标乘-1，得到△A1B1C1 ， 则它与△ABC的位置关系是（ ）A、关于x轴对称 B、关于y轴对称 C、关于直线x=-1对称 D、关于直线y=-1对称