河北省石家庄市桥西区2017年中考数学二模试卷
试卷更新日期:2017-11-07 类型:中考模拟
一、选择题
-
1. 与﹣3的和为0的数是( )A、3 B、﹣3 C、 D、2.
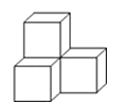
如图是由四个相同的小正方体组成的立体图形,它的左视图为( )
 A、
A、 B、
B、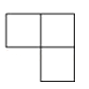 C、
C、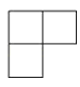 D、
D、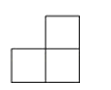 3. 下列计算正确的是( )A、(a2)3=a5 B、a﹣2•a2=a﹣4 C、3 ﹣ =3 D、 =34. 下列图形中由AB∥CD能得到∠1=∠2的是( )A、
3. 下列计算正确的是( )A、(a2)3=a5 B、a﹣2•a2=a﹣4 C、3 ﹣ =3 D、 =34. 下列图形中由AB∥CD能得到∠1=∠2的是( )A、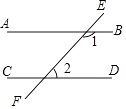 B、
B、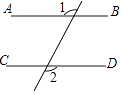 C、
C、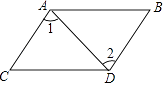 D、
D、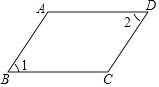 5. 实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )
5. 实数a,b,c在数轴上对应点的位置大致如图所示,则下列式子成立的是( )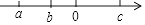 A、ac>bc B、|a﹣b|=a﹣b C、﹣a<﹣b D、a﹣c<b﹣c6. 下列关于菱形、矩形的说法正确的是( )A、菱形的对角线相等且互相平分 B、矩形的对角线相等且互相平分 C、对角线互相垂直的四边形是菱形 D、对角线相等的四边形是矩形7. 化简 的结果是( )A、 B、 C、 D、2x+28. 如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
A、ac>bc B、|a﹣b|=a﹣b C、﹣a<﹣b D、a﹣c<b﹣c6. 下列关于菱形、矩形的说法正确的是( )A、菱形的对角线相等且互相平分 B、矩形的对角线相等且互相平分 C、对角线互相垂直的四边形是菱形 D、对角线相等的四边形是矩形7. 化简 的结果是( )A、 B、 C、 D、2x+28. 如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )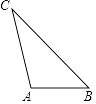 A、三条高的交点 B、三条中线的交点 C、三边垂直平分线的交点 D、三个内角角平分线的交点9. 下列关于一次函数y=﹣2x+1的说法,其中正确的是( )A、图象经过第一、二、三象限 B、图象经过点(﹣2,1) C、当x>1时,y<0 D、y随x的增大而增大10. 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
A、三条高的交点 B、三条中线的交点 C、三边垂直平分线的交点 D、三个内角角平分线的交点9. 下列关于一次函数y=﹣2x+1的说法,其中正确的是( )A、图象经过第一、二、三象限 B、图象经过点(﹣2,1) C、当x>1时,y<0 D、y随x的增大而增大10. 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:步骤1:分别以点A,D为圆心,以大于 AD的长为半径,在AD两侧作弧,两弧交于点M,N;
步骤2:连接MN,分别交AB,AC于点E,F;
步骤3:连接DE,DF.
下列叙述不一定成立的是( )
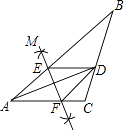 A、线段DE是△ABC的中位线 B、四边形AFDE是菱形 C、MN垂直平分线段AD D、 =11. 某工厂2015年产品的产量为100吨,该产品产量的年平均增长率为x(x>0),设2017年该产品的产量为y吨,则y关于x的函数关系式为( )A、y=100(1﹣x)2 B、y=100(1+x)2 C、y= D、y=100+100(1+x)+100(1+x)212. 如图,点B是⊙O的劣弧 上一点,连接AB,AC,OB,OC,AC交OB于点D,若∠A=36°,∠C=27°,则∠B=( )
A、线段DE是△ABC的中位线 B、四边形AFDE是菱形 C、MN垂直平分线段AD D、 =11. 某工厂2015年产品的产量为100吨,该产品产量的年平均增长率为x(x>0),设2017年该产品的产量为y吨,则y关于x的函数关系式为( )A、y=100(1﹣x)2 B、y=100(1+x)2 C、y= D、y=100+100(1+x)+100(1+x)212. 如图,点B是⊙O的劣弧 上一点,连接AB,AC,OB,OC,AC交OB于点D,若∠A=36°,∠C=27°,则∠B=( ) A、81° B、72° C、60° D、63°13. 如图,一支反比例函数y= 的图象经过点A,作AB⊥x轴于点B,连接OA,若S△AOB=3,则k的值为( )
A、81° B、72° C、60° D、63°13. 如图,一支反比例函数y= 的图象经过点A,作AB⊥x轴于点B,连接OA,若S△AOB=3,则k的值为( ) A、﹣3 B、3 C、﹣6 D、614. 关于x的方程mx2﹣4x﹣m+5=0,有以下说法:
A、﹣3 B、3 C、﹣6 D、614. 关于x的方程mx2﹣4x﹣m+5=0,有以下说法:①当m=0时,方程只有一个实数根;②当m=1时,方程有两个相等的实数根;③当m=﹣1时,方程没有实数根.则其中正确的是( )
A、①② B、①③ C、②③ D、①②③15. 小华进行了5次射击训练后,计算出这5次射击的平均成绩为8环,方差为s12 , 随后小华又进行了第6次射击,成绩恰好是8环,并计算出这6次射击成绩的方差为s22 , 则下列说法正确的是( )
A、s12=s22 B、s12<s22 C、s12>s22 D、无法确定s12与s22的大小16. 如图1,在等边△ABC中,点D,E分别是BC,AC边上的中点,点P为AB边上的一个动点,设AP=x,连接PE,PD,PC,DE,其中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是( )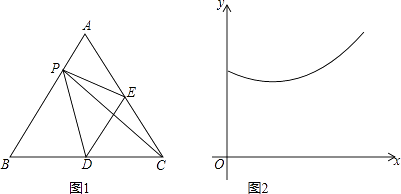 A、线段PE B、线段PD C、线段PC D、线段DE
A、线段PE B、线段PD C、线段PC D、线段DE二、填空题
-
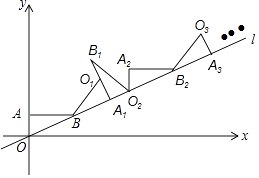
17. 计算: = .18. 一个n边形的内角和是其外角和的2倍,则n= .19. 如图,直线l经过平面直角坐标系的原点O,且与x轴正方向的夹角是30°,点A的坐标是(0,1),点B在直线l上,且AB∥x轴,则点B的坐标是 , 现将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线l上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线l上,顺次旋转下去…,则点A6的横坐标是 .
三、解答题
-
20. 定义新运算:对于任意实数a,b(其中a≠0),都有a⊗b= ﹣ ,等式右边是通常的加法、减法及除法运算,例如2⊗3= ﹣ = + =1.(1)、求(﹣2)⊗3的值;(2)、若x⊗2=1,求x的值.21. 如图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.
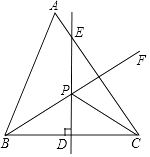 (1)、若∠ACP=24°,求∠ABP的度数;(2)、若∠ACP=m°,∠ABP=n°,请直接写出m,n满足的关系式: .22. 某校组织甲、乙两队开展“保护生态环境知识竞赛”,满分为10分,得分均为整数,规定得分达到6分及以上为合格,达到9分及以上为优秀,如图是甲、乙两队学生这次竞赛成绩分布条形统计图.
(1)、若∠ACP=24°,求∠ABP的度数;(2)、若∠ACP=m°,∠ABP=n°,请直接写出m,n满足的关系式: .22. 某校组织甲、乙两队开展“保护生态环境知识竞赛”,满分为10分,得分均为整数,规定得分达到6分及以上为合格,达到9分及以上为优秀,如图是甲、乙两队学生这次竞赛成绩分布条形统计图.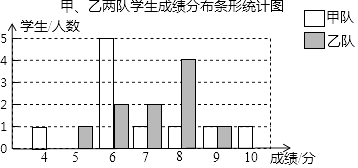
根据以上信息,请解答下面的问题:
(1)、在下面甲、乙两队的成绩统计表中,a= , b=c= .平均分
中位数
众数
方差
合格率
优秀率
甲队
a
6
c
2.76
90%
20%
乙队
7.2
b
8
1.36
80%
10%
(2)、小华同学说:“我在这次比赛中得到了7分,这在我所在的小队成绩中属于中等偏上的位置!”观察(1)中的表格,小华是队的学生;(填“甲”或“乙”)
(3)、甲队同学认为:甲队的合格率、优秀率均高于乙队,所以甲队的成绩好于乙队.但乙队同学不同意甲队同学的说法,认为乙队的成绩要好于甲队.请你写出两条支持乙队同学观点的理由.(4)、学校要从从甲、乙两队获得优秀的学生中,选取两名同学参加市级比赛,则恰好同时选中的两人均为甲队学生的概率为 .23. 某营业厅对手机话费业务有如下的优惠:优惠规则:
①用户手机账户原有话费不能低于240元;
②办理业务时,首先从手机账户中一次性扣除240元,并把这240元抵为300元话费,然后将这300元话费分12次,在每月的15号等额返还到手机账户;
③每月1号从手机账户中扣除话费49元,当月不再扣除其他任何费用;
④每月1号手机账户的话费余额不足以扣除49元时,视为欠费,则当月不再返还等额的话费.
小明的手机账户中原有话费400元,办理了这项优惠业务,设小明的手机账户中每个月末的话费余额是y(元),月数为x(个),则
(1)、每个月等额返还的话费是元,第2个月末的话费余额是元;(2)、求y关于x的函数关系式;(3)、若不续费,小明的手机第几个月会欠费?24. 在菱形ABCD中,AB=2 ,AC是对角线,∠B=60°,点E在BC边上,点F在DC边上,且∠EAF=60°,AE与DC的延长线交于点M,AF与BC的延长线交于点N.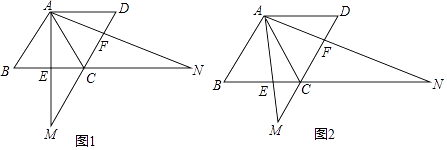 (1)、如图1,若点E为BC边上的中点.
(1)、如图1,若点E为BC边上的中点.①求证:△ACM≌△ACN;
(2)、如图2,若点E为BC边上的任意点(不与点B,C重合),请说明CM•NC是一个定值.25. 抛物线L:y=a(x﹣x1)(x﹣x2)(常数a≠0)与x轴交于点A(x1 , 0),B(x2 , 0),与y轴交于点C,且x1•x2<0,AB=4,当直线l:y=﹣3x+t+2(常数t>0)同时经过点A,C时,t=1.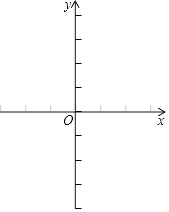 (1)、点C的坐标是;(2)、求点A,B的坐标及L的顶点坐标;(3)、在如图2 所示的平面直角坐标系中,画出L的大致图象;(4)、将L向右平移t个单位长度,平移后y随x的增大而增大部分的图象记为G,若直线l与G有公共点,直接写出t的取值范围.26. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点M在AC边上,点N从点C出发沿折线CB﹣BA运动到点A停止,点P是点C关于直线MN的对称点,连接MP,NP(当点N与点C,A重合时,点P均与点C重合).
(1)、点C的坐标是;(2)、求点A,B的坐标及L的顶点坐标;(3)、在如图2 所示的平面直角坐标系中,画出L的大致图象;(4)、将L向右平移t个单位长度,平移后y随x的增大而增大部分的图象记为G,若直线l与G有公共点,直接写出t的取值范围.26. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点M在AC边上,点N从点C出发沿折线CB﹣BA运动到点A停止,点P是点C关于直线MN的对称点,连接MP,NP(当点N与点C,A重合时,点P均与点C重合). (1)、若CM=2,
(1)、若CM=2,①又当点N在CB上,MP∥BC时,则CN= , MN=;
(2)、在(1)的条件下,求点P到AB边的距离的最小值,并求出当取得这个最小值时,点P运动路线的长是多少?(参考数据:sin54°=cos36°≈ ,sin36°=cos54°≈ ,结果保留π)(3)、设MC=a(a>2),其他条件不变,当有且只能有唯一的点P落在线段AB上时,直接写出a的取值范围 .