-
1、已知 , 为复数,则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则或 D、若 , 则
-
2、锐角中,角A、B、C的对边分别为、、 , 满足 , 若存在最大值,则实数的取值范围是( )A、 B、 C、 D、
-
3、如图,在中,已知 , , , , 分别是 , 边上的点,且 , , 且 , 若线段 , 的中点分别为 , , 则的最小值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、设O是坐标原点,单位圆O上一点A,射线OA绕着O点逆时针旋转后得到OP,P为与单位圆的交点,P的坐标为 , 则A的坐标为( )A、 B、 C、 D、
-
5、定义在上的函数 , 若 , , , 则a,b,c的大小关系为( )A、 B、 C、 D、
-
6、设 , , 其中为虚数单位.则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
7、在中,下列等式一定成立的是( )A、 B、 C、 D、
-
8、已知单位向量满足 , 则在上的投影向量为( )A、 B、 C、 D、
-
9、已知实数集合 , , 若 , 则( )A、 B、0 C、1 D、2
-
10、地区生产总值(地区)是衡量一个地区经济发展的重要指标,在过去五年(2019年-2023年)中,某地区的地区生产总值实现了“翻一番”的飞跃,从1464亿元增长到了3008亿元,若该地区在这五年中的年份编号x(2019年对应的 x值为1,2020 年对应的x值为2,以此类推)与地区生产总值y(百亿元)的对应数据如下表:
年份编号x
1
2
3
4
5
地区生产总值y(百亿元)
14.64
17.42
20.72
25.20
30.08
(1)、该地区2023年的人均生产总值为9.39 万元,若2023年全国的人均生产总值X(万元)服从正态分布 , 那么在全国其他城市或地区中随机挑选2 个,记随机变量 Y为“2023年人均生产总值高于该地区的城市或地区的数量”,求 的概率;(2)、该地区的人口总数t(百万人)与年份编号x的回归方程可以近似为 , 根据上述的回归方程,估算该地区年份编号x与人均生产总值(人均)u(万元)之间的线性回归方程.参考公式与数据:人均生产总值=地区生产总值÷人口总数;
线性回归方程中,斜率和截距的最小二乘法估计公式分别是: ,
若 , 则.
-
11、如图,在三棱锥中,是边长等于2的正三角形, , 为的中点.
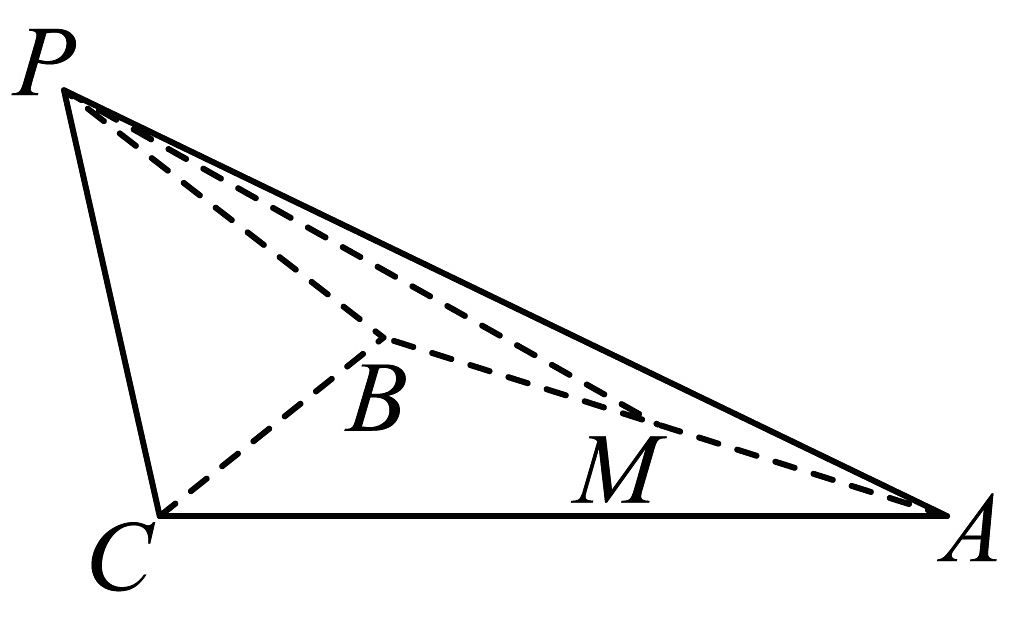 (1)、求证:;(2)、若 , 求点到平面的距离.
(1)、求证:;(2)、若 , 求点到平面的距离. -
12、已知函数 , 曲线在处与直线相切.(1)、求、的值;(2)、求在上的最大值和最小值.(其中为自然对数的底数)
-
13、已知是锐角,若 , 则 .
-
14、已知公差不为0的等差数列的前项和为 , 且是与的等比中项,则下列说法正确的是( )A、 B、 C、数列是递增数列 D、当时,的最大值为8
-
15、在四棱锥中,分别是上的点, , 则下列条件可以确定平面的是( )A、 B、 C、平面 D、平面
-
16、已知二项展开式 , 则( )A、 B、 C、 D、
-
17、已知数列满足 , 若 , 则的取值范围是( )A、 B、 C、 D、
-
18、已知随机变量 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
19、扇形的半径等于2,面积等于6,则它的圆心角等于( )A、1 B、 C、3 D、6
-
20、双曲线的一个焦点为 , 则( )A、 B、 C、3 D、