-
1、地区生产总值(地区)是衡量一个地区经济发展的重要指标,在过去五年(2019年-2023年)中,某地区的地区生产总值实现了“翻一番”的飞跃,从1464亿元增长到了3008亿元,若该地区在这五年中的年份编号x(2019年对应的 x值为1,2020 年对应的x值为2,以此类推)与地区生产总值y(百亿元)的对应数据如下表:
年份编号x
1
2
3
4
5
地区生产总值y(百亿元)
14.64
17.42
20.72
25.20
30.08
(1)、该地区2023年的人均生产总值为9.39 万元,若2023年全国的人均生产总值X(万元)服从正态分布 , 那么在全国其他城市或地区中随机挑选2 个,记随机变量 Y为“2023年人均生产总值高于该地区的城市或地区的数量”,求 的概率;(2)、该地区的人口总数t(百万人)与年份编号x的回归方程可以近似为 , 根据上述的回归方程,估算该地区年份编号x与人均生产总值(人均)u(万元)之间的线性回归方程.参考公式与数据:人均生产总值=地区生产总值÷人口总数;
线性回归方程中,斜率和截距的最小二乘法估计公式分别是: ,
若 , 则.
-
2、如图,在三棱锥中,是边长等于2的正三角形, , 为的中点.
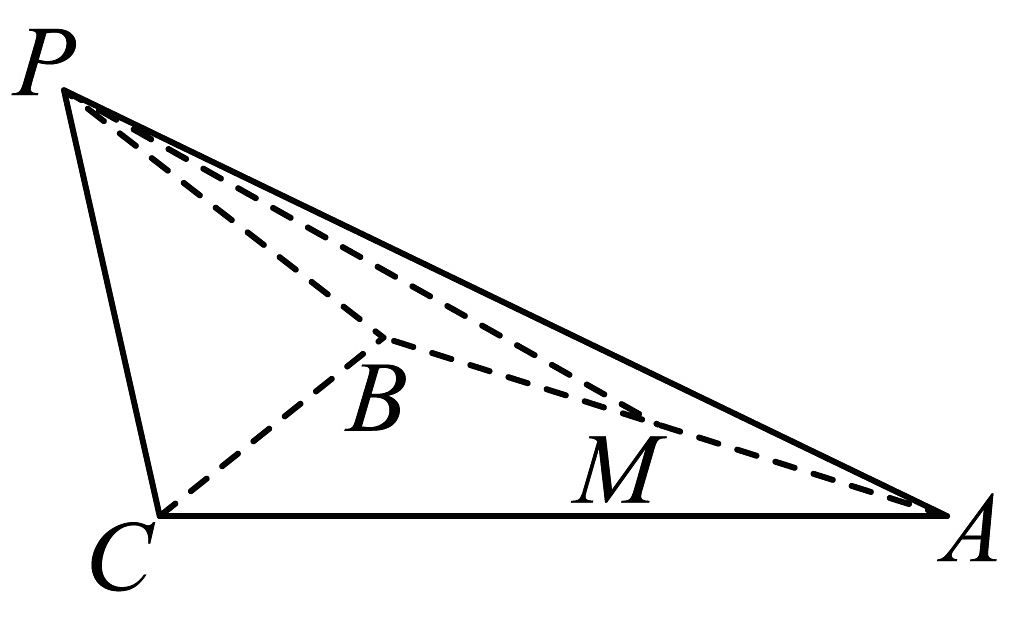 (1)、求证:;(2)、若 , 求点到平面的距离.
(1)、求证:;(2)、若 , 求点到平面的距离. -
3、已知函数 , 曲线在处与直线相切.(1)、求、的值;(2)、求在上的最大值和最小值.(其中为自然对数的底数)
-
4、已知是锐角,若 , 则 .
-
5、已知公差不为0的等差数列的前项和为 , 且是与的等比中项,则下列说法正确的是( )A、 B、 C、数列是递增数列 D、当时,的最大值为8
-
6、在四棱锥中,分别是上的点, , 则下列条件可以确定平面的是( )A、 B、 C、平面 D、平面
-
7、已知二项展开式 , 则( )A、 B、 C、 D、
-
8、已知数列满足 , 若 , 则的取值范围是( )A、 B、 C、 D、
-
9、已知随机变量 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
10、扇形的半径等于2,面积等于6,则它的圆心角等于( )A、1 B、 C、3 D、6
-
11、双曲线的一个焦点为 , 则( )A、 B、 C、3 D、
-
12、记复数的共轭复数为 , 若 , 则( )A、 B、 C、 D、
-
13、已知集合 , 集合 , 则( )A、 B、 C、 D、
-
14、函数的定义域为.
-
15、为了避免就餐聚集和减少排队时间,某校开学后,食堂从开学第一天起,每餐只推出即点即取的米饭套餐和面食套餐.已知某同学每天中午会在食堂提供的两种套餐中选择,已知他第一天选择米饭套餐的概率为 , 而前一天选择了米饭套餐后一天继续选择米饭套餐的概率为 , 前一天选择面食套餐后一天继续选择面食套餐的概率为 , 如此往复.
(1)求该同学第二天中午选择米饭套餐的概率;
(2)记该同学第天选择米饭套餐的概率为 .
(i)证明:为等比数列;
(ii)证明:当时, .
-
16、如图所示,某小区为美化环境,准备在小区内的草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数的图象的一部分,后一段DBC是函数( , , , )的图象,图象的最高点为 , 且 , 垂足为点F.
 (1)、求函数()的解析式;(2)、若在草坪内修建如图所示的矩形儿童乐园PMFE,点P在曲线OD上,其横坐标为 , 点E在OC上,求儿童乐园的面积.
(1)、求函数()的解析式;(2)、若在草坪内修建如图所示的矩形儿童乐园PMFE,点P在曲线OD上,其横坐标为 , 点E在OC上,求儿童乐园的面积. -
17、已知函数 .
求函数的单调减区间;
将函数的图象向左平移个单位,再将所得的图象上各点的横坐标缩短为原来的倍,纵坐标不变,得到函数的图象,求在上的值域.
-
18、已知.
(1)求的值;
(2)求的值.
-
19、已知的内角所对的边分别是 , 若 , , 则角为.
-
20、已知向量 , , , 则下列结论中正确的是( )A、 B、 C、 D、