北京市西城区2016-2017学年高考理数二模考试试卷

试卷更新日期：2017-09-13 类型：高考模拟

进入出卷网下载

一、选择题

1. 在复平面内，复数z对应的点是Z（1，﹣2），则复数z的共轭复数 $\bar{z}$ =（）

A、1+2i B、1﹣2i C、2+i D、2﹣i

查看试题解析
2. 下列函数中，值域为[0，1]的是（）

A、y=x² B、y=sinx C、 $y = \frac{1}{x^{2} + 1}$ D、 $y = \sqrt{1 - x^{2}}$

查看试题解析
3. 在极坐标系中，圆ρ=sinθ的圆心的极坐标是（）

A、 $(1 ， \frac{π}{2})$ B、（1，0） C、 $(\frac{1}{2} ， \frac{π}{2})$ D、 $(\frac{1}{2} ， 0)$

查看试题解析
4. 在平面直角坐标系中，不等式组 ${\begin{matrix} 3 x - 2 y \geq 0 \\ 3 x - y - 3 \leq 0 \\ y \geq 0 \end{matrix}$ 表示的平面区域的面积是（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
5. 设双曲线 $\frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}}$ =1（a＞0，b＞0）的离心率是3，则其渐近线的方程为（）

A、 $x \pm 2 \sqrt{2} y = 0$ B、 $2 \sqrt{2} x \pm y = 0$ C、x±8y=0 D、8x±y=0

查看试题解析
6. 设 $\vec{a}$ ， $\vec{b}$ 是平面上的两个单位向量， $\vec{a}$ • $\vec{b}$ = $\frac{3}{5}$ ．若m∈R，则| $\vec{a}$ +m $\vec{b}$ |的最小值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{4}{5}$ D、 $\frac{5}{4}$

查看试题解析
7. 函数f（x）=x|x|．若存在x∈[1，+∞），使得f（x﹣2k）﹣k＜0，则k的取值范围是（）

A、（2，+∞） B、（1，+∞） C、（ $\frac{1}{2}$ ，+∞） D、（ $\frac{1}{4}$ ，+∞）

查看试题解析
8. 有三支股票A，B，C，28位股民的持有情况如下：每位股民至少持有其中一支股票．在不持有A股票的人中，持有B股票的人数是持有C股票的人数的2倍．在持有A股票的人中，只持有A股票的人数比除了持有A股票外，同时还持有其它股票的人数多1．在只持有一支股票的人中，有一半持有A股票．则只持有B股票的股民人数是（）

A、7 B、6 C、5 D、4

查看试题解析

二、填空题

9. 执行如图所示的程序框图，输出的S值为．

查看试题解析
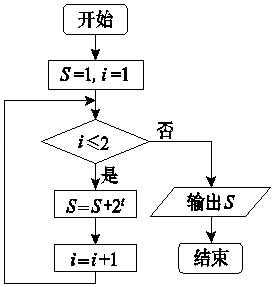10. 已知等差数列{a_n}的公差为2，且a₁ ， a₂ ， a₄成等比数列，则a₁=；数列{a_n}的前n项和S_n= ．

查看试题解析
11. 在△ABC中，角A、B、C的对边边长分别是a、b、c，若 $A = \frac{π}{3}$ ， $a = \sqrt{3}$ ，b=1，则c的值为．

查看试题解析
12. 函数f（x）= ${\begin{matrix} 2^{x} ， x \leq 0 \\ l o g_{2} x ， x > 0. \end{matrix}$ 则 $f (\frac{1}{4})$ =；方程f（﹣x）= $\frac{1}{2}$ 的解是．

查看试题解析
13. 大厦一层有A，B，C，D四部电梯，3人在一层乘坐电梯上楼，其中2人恰好乘坐同一部电梯，则不同的乘坐方式有种．（用数字作答）

查看试题解析
14. 在空间直角坐标系O﹣xyz中，四面体A﹣BCD在xOy，yOz，zOx坐标平面上的一组正投影图形如图所示（坐标轴用细虚线表示）．该四面体的体积是．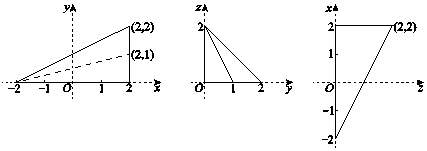

查看试题解析

三、解答题

15. 已知函数 $f (x) = t a n (x + \frac{π}{4})$ ．
（Ⅰ）求f（x）的定义域；
（Ⅱ）设β∈（0，π），且 $f (β) = 2 c o s (β - \frac{π}{4})$ ，求β的值．

查看试题解析
16. 如图，在几何体ABCDEF中，底面ABCD为矩形，EF∥CD，AD⊥FC．点M在棱FC上，平面ADM与棱FB交于点N．
（Ⅰ）求证：AD∥MN；
（Ⅱ）求证：平面ADMN⊥平面CDEF；
（Ⅲ）若CD⊥EA，EF=ED，CD=2EF，平面ADE∩平面BCF=l，求二面角A﹣l﹣B的大小．

查看试题解析
17. 某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．整理评分数据，将分数以10为组距分成6组：[0，10），[10，20），[20，30），[30，40），[40，50），[50，60]，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：
B餐厅分数频数分布表
分数区间
频数
[0，10）
2
[10，20）
3
[20，30）
5
[30，40）
15
[40，50）
40
[50，60]
35
定义学生对餐厅评价的“满意度指数”如下：
分数
[0，30）
[30，50）
[50，60]
满意度指数
0
1
2
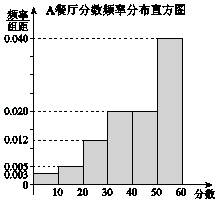
（Ⅰ）在抽样的100人中，求对A餐厅评价“满意度指数”为0的人数；
（Ⅱ）从该校在A，B两家餐厅都用过餐的学生中随机抽取1人进行调查，试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率；
（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．

查看试题解析
18. 在平面直角坐标系xOy中，抛物线C的顶点是原点，以x轴为对称轴，且经过点P（1，2）．
（Ⅰ）求抛物线C的方程；
（Ⅱ）设点A，B在抛物线C上，直线PA，PB分别与y轴交于点M，N，|PM|=|PN|．求直线AB的斜率．

查看试题解析
19. 已知函数f（x）=（x²+ax﹣a）•e¹^﹣x ，其中a∈R．
（Ⅰ）求函数f'（x）的零点个数；
（Ⅱ）证明：a≥0是函数f（x）存在最小值的充分而不必要条件．

查看试题解析
20. 设集合A_2n={1，2，3，…，2n}（n∈N^* ， n≥2）．如果对于A_2n的每一个含有m（m≥4）个元素的子集P，P中必有4个元素的和等于4n+1，称正整数m为集合A_2n的一个“相关数”．
（Ⅰ）当n=3时，判断5和6是否为集合A₆的“相关数”，说明理由；
（Ⅱ）若m为集合A_2n的“相关数”，证明：m﹣n﹣3≥0；
（Ⅲ）给定正整数n．求集合A_2n的“相关数”m的最小值．

查看试题解析

B餐厅分数频数分布表
分数区间	频数
[0，10）	2
[10，20）	3
[20，30）	5
[30，40）	15
[40，50）	40
[50，60]	35

分数	[0，30）	[30，50）	[50，60]
满意度指数	0	1	2