北京市海淀区2017-2018学年高一上学期理数期中考试试卷

试卷更新日期：2017-12-04 类型：期中考试

进入出卷网下载

一、选择题

1. 若集合A={x|x﹣2＜0}，B={x|e^x＞1}，则A∩B=（）

A、R B、（﹣∞，2） C、（0，2） D、（2，+∞）

查看试题解析
2. 下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（）

A、f（x）=ln|x| B、f（x）=2^﹣x C、f（x）=x³ D、f（x）=﹣x²

查看试题解析
3. 已知向量 $\vec{a}$ =（1，0）， $\vec{b}$ =（﹣1，1），则（）

A、 $\vec{a}$ ∥ $\vec{b}$ B、 $\vec{a}$ ⊥ $\vec{b}$ C、（ $\vec{a} - \vec{b}$ ）∥ $\vec{b}$ D、（ $\vec{a} + \vec{b}$ ）⊥ $\vec{a}$

查看试题解析
4. 已知数列{a_n}满足a₁+a₂+…+a_n=2a₂（n=1，2，3，…），则（）

A、a₁＜0 B、a₁＞0 C、a₁≠a₂ D、a₂=0

查看试题解析
5. 将 $y = s i n (2 x + \frac{π}{6})$ 的图象向左平移 $\frac{π}{6}$ 个单位，则所得图象的函数解析式为（）

A、y=sin2x B、y=cos2x C、 $y = s i n (2 x + \frac{π}{3})$ D、 $y = s i n (2 x - \frac{π}{6})$

查看试题解析
6. 设α∈R，则“α是第一象限角”是“sinα+cosα＞1”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
7. 设f（x）=e^sinx+e^﹣sinx（x∈R），则下列说法不正确的是（）

A、f（x）为R上偶函数 B、π为f（x）的一个周期 C、π为f（x）的一个极小值点 D、f（x）在区间 $(0 ， \frac{π}{2})$ 上单调递减

查看试题解析
8. 已知非空集合A，B满足以下两个条件．
（ⅰ）A∪B={1，2，3，4，5，6}，A∩B=∅；
（ⅱ）A的元素个数不是A中的元素，B的元素个数不是B中的元素，则有序集合对（A，B）的个数为（）

A、10 B、12 C、14 D、16

查看试题解析

二、填空题

9. 定积分 $\int_{- 1}^{1} x^{3} d x$ 的值等于．

查看试题解析
10. 设在海拔x（单位：m）处的大气压强y（单位：kPa），y与x的函数关系可近似表示为y=100e^ax ，已知在海拔1000m处的大气压强为90kPa，则根据函数关系式，在海拔2000m处的大气压强为 kPa．

查看试题解析
11. 能够说明“设x是实数，若x＞1，则 $x + \frac{1}{x - 1} > 3$ ”是假命题的一个实数x的值为．

查看试题解析
12. 已知△ABC是边长为2的正三角形，O、D分别为边AB、BC的中点，则
① $\vec{A D} \cdot \vec{A C}$ =；
②若 $\vec{O C} = x \vec{A B} + y \vec{A D}$ ，则x+y= ．

查看试题解析
13. 已知函数 $f (x) = \frac{1}{s i n (ω x + φ)}$ （其中ω＞0， $| φ | < \frac{π}{2}$ ）的部分图象如图所示，则ω= ， φ= ．

查看试题解析
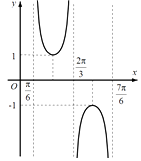14. 已知函数f（x）是定义在R上的奇函数，当x＞0时，f（x）=x²﹣ax+a，其中a∈R．
①f（﹣1）=；
②若f（x）的值域是R，则a的取值范围是．

查看试题解析

三、解答题

15. 已知函数 $f (x) = 2 \sqrt{2} c o s x s i n (x + \frac{π}{4}) - 1$ ．
（Ⅰ）求 $f (\frac{π}{4})$ 的值；
（Ⅱ）求f（x）在区间 $[0 ， \frac{π}{2}]$ 上的最大值和最小值．

查看试题解析
16. 已知{a_n}是等比数列，满足a₂=6，a₃=﹣18，数列{b_n}满足b₁=2，且{2b_n+a_n}是公差为2的等差数列．
（Ⅰ）求数列{a_n}和{b_n}的通项公式；
（Ⅱ）求数列{b_n}的前n项和．

查看试题解析
17. 已知函数 $f (x) = x - (a + 1) l n x - \frac{a}{x}$ ，其中a＞0．
（Ⅰ）当a=2时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）求f（x）在区间[1，e]上的最小值．（其中e是自然对数的底数）

查看试题解析
18. 如图，在四边形ACBD中， $c o s ∠ C A D = - \frac{1}{7}$ ，且△ABC为正三角形．
（Ⅰ）求cos∠BAD的值；
（Ⅱ）若CD=4， $B D = \sqrt{3}$ ，求AB和AD的长．

查看试题解析
19. 已知函数 $f (x) = \sqrt{2} e^{x} s i n x$ （0＜x＜π），g（x）=（x﹣1）lnx+m（m∈R）
（Ⅰ）求f（x）的单调区间；
（Ⅱ）求证：1是g（x）的唯一极小值点；
（Ⅲ）若存在a，b∈（0，π），满足f（a）=g（b），求m的取值范围．（只需写出结论）

查看试题解析
20. 若数列A：a₁ ， a₂ ， …，a_n（n≥3）中a_i∈N^*（1≤i≤n）且对任意的2≤k≤n﹣1，a_k+1+a_k_﹣1＞2a_k恒成立，则称数列A为“U﹣数列”．
（Ⅰ）若数列1，x，y，7为“U﹣数列”，写出所有可能的x，y；
（Ⅱ）若“U﹣数列”A：a₁ ， a₂ ， …，a_n中，a₁=1，a_n=2017，求n的最大值；
（Ⅲ）设n₀为给定的偶数，对所有可能的“U﹣数列”A：a₁ ， a₂ ， …，a_n0 ，记M=max{a₁ ， a₂ ， …，a_n0}，其中max{x₁ ， x₂ ， …，x_s}表示x₁ ， x₂ ， …，x_s这s个数中最大的数，求M的最小值．

查看试题解析