北京市海淀区2016-2017学年高考文数二模考试试卷

试卷更新日期：2017-09-13 类型：高考模拟

进入出卷网下载

一、选择题

1. 若集合A={﹣2，0，1}，B={x|x＜﹣1或x＞0}，则A∩B=（）

A、{﹣2} B、{1} C、{﹣2，1} D、{﹣2，0，1}

查看试题解析
2. 在复平面内，复数 $z = \frac{2 i}{1 - i}$ 对应的点的坐标为（）

A、（1，﹣1） B、（1，1） C、（﹣1，1） D、（﹣1，﹣1）

查看试题解析
3. 已知向量 $\vec{a}$ =（x，1）， $\vec{b}$ =（3，﹣2），若 $\vec{a}$ ∥ $\vec{b}$ ，则x=（）

A、﹣3 B、 $- \frac{3}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
4. 执行如图所示的程序框图，若输入a=﹣7，d=3，则输出的S为（）

A、S=﹣12 B、S=﹣11 C、S=﹣10 D、S=﹣6

查看试题解析
5. 已知数列{a_n}是等比数列，则“a₂＞a₁”是“数列{a_n}为递增数列”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
6. 北京市2016年12个月的PM2.5平均浓度指数如图所示．由图判断，四个季度中PM2.5的平均浓度指数方差最小的是（）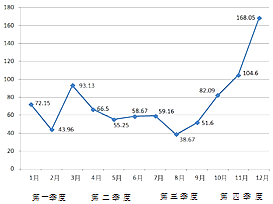

A、第一季度 B、第二季度 C、第三季度 D、第四季度

查看试题解析
7. 函数y=f（x）的图象如图所示，则f（x）的解析式可以为（）

A、 $f (x) = \frac{1}{x} - x^{2}$ B、 $f (x) = \frac{1}{x} - x^{3}$ C、 $f (x) = \frac{1}{x} - e^{x}$ D、 $f (x) = \frac{1}{x} - l n x$

查看试题解析
8. 一位手机用户前四次输入四位数字手机密码均不正确，第五次输入密码正确，手机解锁．事后发现前四次输入的密码中，每次都有两个数字正确，但它们各自的位置均不正确．已知前四次输入密码分别为3406，1630，7364，6173，则正确的密码中一定含有数字（）

A、4，6 B、3，6 C、3，7 D、1，7

查看试题解析

二、填空题

9. 双曲线 $x^{2} - \frac{y^{2}}{9} = 1$ 的实轴长为．

查看试题解析
10. 在log₂3，2^﹣3 ， cosπ这三个数中最大的数是．

查看试题解析
11. 在△ABC中，a=2，b=3，c=4，则其最大内角的余弦值为．

查看试题解析
12. 设D为不等式（x﹣1）²+y²≤1表示的平面区域，直线x+ $\sqrt{3}$ y+b=0与区域D有公共点，则b的取值范围是．

查看试题解析
13. 已知O为原点，点P为直线2x+y﹣2=0上的任意一点．非零向量 $\vec{a}$ =（m，n）．若 $\vec{O P}$ • $\vec{a}$ 恒为定值，则 $\frac{m}{n}$ = ．

查看试题解析
14. 如图，在棱长为1的正方体ABCD﹣A₁B₁C₁D₁中，点P是线段BD₁上的动点．当△PAC在平面DC₁ ， BC₁ ， AC上的正投影都为三角形时，将它们的面积分别记为S₁ ， S₂ ， S₃ ．
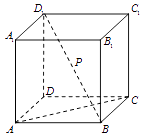
（i）当BP= $\frac{\sqrt{3}}{3}$ 时，S₁S₂（填“＞”或“=”或“＜”）；
（ii） S₁+S₂+S₃的最大值为．

查看试题解析

三、解答题

15. 已知函数f（x）=sin2xcos $\frac{π}{5} - c o s 2 x s i n \frac{π}{5}$ ．
（Ⅰ）求函数f（x）的最小正周期和对称轴的方程；
（Ⅱ）求函数f（x）在区间 $[0 ， \frac{π}{2}]$ 上的最大值．

查看试题解析
16. 已知{a_n}是各项为正数的等差数列，S_n为其前n项和，且4S_n=（a_n+1）² ．
（Ⅰ）求a₁ ， a₂的值及{a_n}的通项公式；
（Ⅱ）求数列 ${S_{n} - \frac{7}{2} a_{n}}$ 的最小值．

查看试题解析
17. 为了响应教育部颁布的《关于推进中小学生研学旅行的意见》，某校计划开设八门研学旅行课程，并对全校学生的选课意向进行调查（调查要求全员参与，每个学生必须从八门课程中选出唯一一门课程）．本次调查结果如下．图中，课程A，B，C，D，E为人文类课程，课程F，G，H为自然科学类课程．为进一步研究学生选课意向，结合上面图表，采取分层抽样方法从全校抽取1%的学生作为研究样本组（以下简称“组M”）．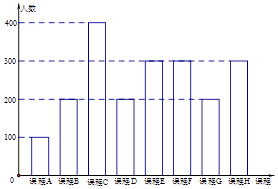
（Ⅰ）在“组M”中，选择人文类课程和自然科学类课程的人数各有多少？
（Ⅱ）某地举办自然科学营活动，学校要求：参加活动的学生只能是“组M”中选择F课程或G课程的同学，并且这些同学以自愿报名缴费的方式参加活动．选择F课程的学生中有x人参加科学营活动，每人需缴纳2000元，选择G课程的学生中有y人参加该活动，每人需缴纳1000元．记选择F课程和G课程的学生自愿报名人数的情况为（x，y），参加活动的学生缴纳费用总和为S元．
（ⅰ）当S=4000时，写出（x，y）的所有可能取值；
（ⅱ）若选择G课程的同学都参加科学营活动，求S＞4500元的概率．

查看试题解析
18. 如图，在四棱锥P﹣ABCD中，底面ABCD为菱形，PC⊥平面ABCD，点E在棱PA上．
（Ⅰ）求证：直线BD⊥平面PAC；
（Ⅱ）若PC∥平面BDE，求证：AE=EP；
（Ⅲ）是否存在点E，使得四面体A﹣BDE的体积等于四面体P﹣BDC的体积的 $\frac{1}{3}$ ？若存在，求出 $\frac{P E}{P A}$ 的值；若不存在，请说明理由．

查看试题解析
19. 已知函数f（x）= $\frac{1}{3} x^{3} + \frac{1}{2} x^{2}$ ﹣2x+1．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）当0＜a≤ $\frac{5}{2}$ 时，求函数f（x）在区间[﹣a，a]上的最大值．

查看试题解析
20. 已知F₁（﹣1，0），F₂（1，0）分别是椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{3}$ =1（a＞0）的左、右焦点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若A，B分别在直线x=﹣2和x=2上，且AF₁⊥BF₁ ．
（ⅰ）当△ABF₁为等腰三角形时，求△ABF₁的面积；
（ⅱ）求点F₁ ， F₂到直线AB距离之和的最小值．

查看试题解析