相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知集合 , 则( )A、 B、 C、 D、
-
2、某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底在水平线上,桥与平行,为铅垂线(在上).经测算,若以为轴,为轴建立平面直角坐标系,则左侧曲线上的任一点在抛物线上,而右侧曲线上的任一点在以为顶点的抛物线上.
 (1)、求桥的长度;(2)、计划在谷底两侧建造平行于的桥墩和 , 且为米,其中 , 在上(不包括端点).若桥墩每米的造价为(万元),桥墩每米的造价为(万元),则当为多少米时,两个桥墩的总造价最低?
(1)、求桥的长度;(2)、计划在谷底两侧建造平行于的桥墩和 , 且为米,其中 , 在上(不包括端点).若桥墩每米的造价为(万元),桥墩每米的造价为(万元),则当为多少米时,两个桥墩的总造价最低? -
3、
如图,在中, , 点在边上,.
 (1)求的长度;(2)若 , 求的长度.
(1)求的长度;(2)若 , 求的长度. -
4、在中,角、、的对边分别为、、 , 且满足.(1)、求;(2)、若 , 的面积为 , 求的周长.
-
5、已知函数在上有且仅有2个零点,则的取值范围为 .
-
6、已知 , , 则的值为.
-
7、已知函数 , 为的零点,且在上单调递减,则下列结论正确的是( )A、 B、若 , 则 C、是偶函数 D、的取值范围是
-
8、下列结论正确的是( )A、“”是“”的充分不必要条件 B、命题“ , 成立”的否定是“ , ” C、最小值2 D、若 , 且 , 则
-
9、设函数若存在最小值,则实数a的取值范围为( )A、 B、 C、 D、
-
10、已知 , 其部分图象如图所示,则的解析式为( )
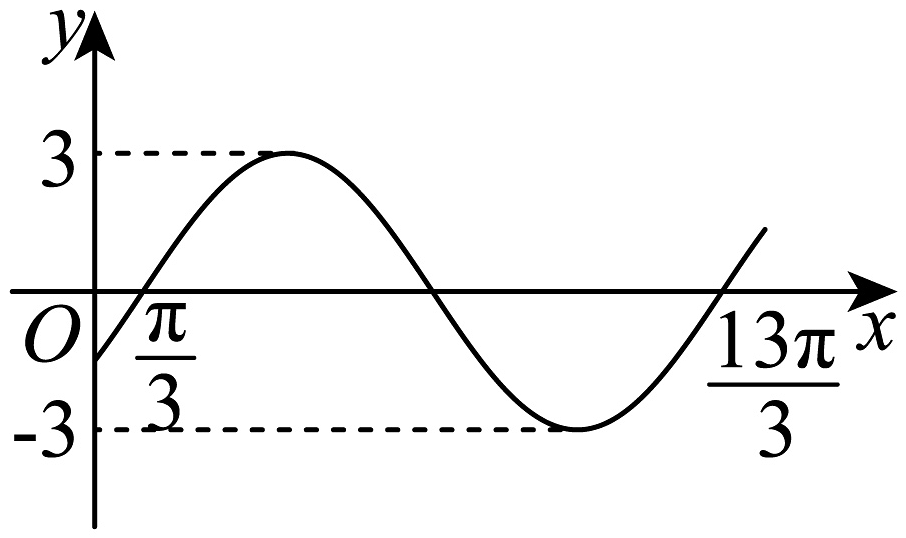 A、 B、 C、 D、
A、 B、 C、 D、 -
11、为了得到函数的图象,可将的图象( )A、向右平移个单位 B、向右平移个单位 C、向左平移个单位 D、向左平移个单位
-
12、若角的终边经过点 , 则的值是( )A、 B、 C、 D、
-
13、函数为幂函数,则该函数为( )A、增函数 B、减函数 C、奇函数 D、偶函数
-
14、曲线在点处的切线方程为.
-
15、已知定点和直线 , 动圆和直线相切,且过点作圆的切线,切线长等于动圆的半径.(1)、求圆的圆心的轨迹方程.(2)、当圆的面积最小时,求圆的方程.
-
16、在中, , , , 分别是上的点,满足且经过的重心,将沿折起到的位置,使 , 是的中点,如图所示.
 (1)、求证:平面;(2)、在线段上是否存在点 , 使平面与平面的夹角的余弦值为 , 若存在,求出的长度;若不存在,请说明理由.
(1)、求证:平面;(2)、在线段上是否存在点 , 使平面与平面的夹角的余弦值为 , 若存在,求出的长度;若不存在,请说明理由. -
17、如图所示,四棱锥的底面是矩形,底面 , , , , .
 (1)、证明:平面;(2)、求直线与平面所成角的余弦值.
(1)、证明:平面;(2)、求直线与平面所成角的余弦值. -
18、我校近几年加大了对学生强基考试的培训,为了选择培训的对象,今年我校进行一次数学考试,从参加考试的同学中,选取50名同学将其成绩(百分制,均为整数)分成六组:第1组 , 第2组 , 第3组 , 第4组 , 第5组 , 第6组 , 得到频率分布直方图(如图),观察图形中的信息,回答下列问题:
 (1)、利用组中值估计本次考试成绩的平均数;(2)、已知学生成绩评定等级有优秀、良好、一般三个等级,其中成绩不小于90分时为优秀等级,若从第5组和第6组两组学生中,随机抽取2人,求所抽取的2人中至少1人成绩优秀的概率.
(1)、利用组中值估计本次考试成绩的平均数;(2)、已知学生成绩评定等级有优秀、良好、一般三个等级,其中成绩不小于90分时为优秀等级,若从第5组和第6组两组学生中,随机抽取2人,求所抽取的2人中至少1人成绩优秀的概率. -
19、在中,分别为三个内角的对边,且(1)、求角A的大小;(2)、若 , , 求和的值.
-
20、在棱长为的正方体中,点、分别是梭、的中点,是侧面上的动点,且平面 , 则点的轨迹长为 , 点到直线的距离的最小值为.