相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、镜片的厚度是由镜片的折射率决定,镜片的折射率越高,镜片越薄,同时镜片越轻,也就会带来更为舒适的佩戴体验.某次社会实践活动中,甲、乙、丙三位同学分别制作了三种不同的树脂镜片,折射率分别为 , 则这三种镜片中,制作出最薄镜片和最厚镜片的同学分别为( )A、丙同学和甲同学 B、乙同学和甲同学 C、甲同学和丙同学 D、乙同学和丙同学
-
2、函数的图象如图所示,则该函数的定义域和单调区间分别是
 A、和 B、和 C、和 D、和
A、和 B、和 C、和 D、和 -
3、如图,把直截面半径为的圆柱形木头锯成直截面为矩形的木料,如果矩形的一边长为(单位:),面积为(单位:),则把表示为的函数的解析式为( )
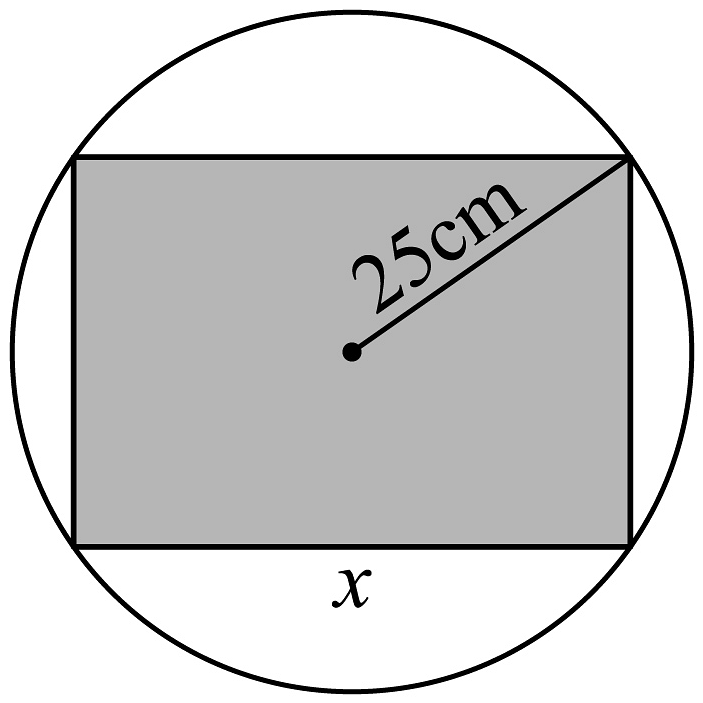 A、 B、 , C、 D、 ,
A、 B、 , C、 D、 , -
4、命题“ , 使得”的否定为( )A、 , B、 , 使得 C、 , D、 , 使得
-
5、已知集合 , 集合 , , 则图中阴影部分表示的集合为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、某服装厂拟在2021年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)m万件与年促销费用万元满足 . 已知2021年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格定为每件产品年平均成本的2倍(此处计算每件产品年平均成本时,产品成本仅包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2021年该产品的利润y万元表示为年促销费用x万元的函数;(利润=收入-成本);
(2)该服装厂2021年的促销费用投入多少万元时,利润最大.
-
7、已知函数.(1)、求的值;(2)、探索;(3)、利用(2)中结论,求的值.
-
8、已知函数是一次函数,且满足.(1)、求的解析式;(2)、若 , 求的最小值.
-
9、解关于的不等式.(1)、;(2)、;(3)、.
-
10、已知全集 .
(1)求;
(2)求 .
-
11、已知定义在上的运算“”: , 若 , 则关于的不等式的解集为.
-
12、已知函数 , 当时,则函数的值域为 , 的最小值是.
-
13、已知集合 , 若 , 则实数a的值可以是( ).A、 B、 C、0 D、
-
14、已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、
-
15、某中学高中学生运动会,一班46名学生中有15名学生没有参加比赛,参加比赛的学生中,参加田赛的有16人,参加径赛的有23人,则田赛和径赛都参加的学生人数为( ).A、7 B、8 C、10 D、12
-
16、下列四组函数,表示同一函数的是( )A、 B、 C、 D、
-
17、不等式的解集为 .
-
18、已知函数则( )A、 B、1 C、2 D、5
-
19、在数列中, , , 对满足的任意正整数m,n,p,q,都有成立.(1)、若数列是等比数列,求a,b满足的条件;(2)、若 , , 设.
①求数列的通项公式;
②求证:.
-
20、在四棱锥中, , , 底面 , 点O在上,且.
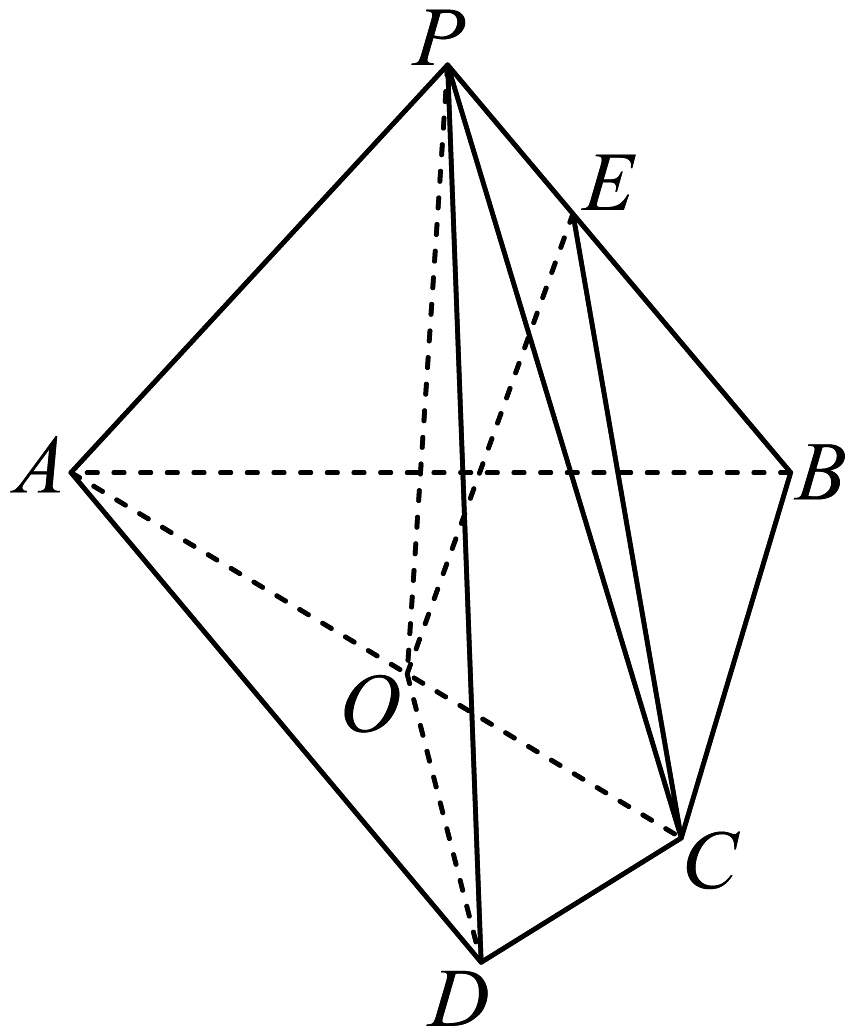 (1)、求证:;(2)、若 , , 点在上,平面 , 求的值;(3)、若 , 二面角的正切值为 , 求二面角的余弦值.
(1)、求证:;(2)、若 , , 点在上,平面 , 求的值;(3)、若 , 二面角的正切值为 , 求二面角的余弦值.