相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知向量 , 且 , 则( )A、1 B、2 C、 D、0
-
2、已知是的共轭复数,则( )A、0 B、 C、2 D、
-
3、已知 , 则( )A、 B、 C、 D、
-
4、曼哈顿距离是一个充满神秘与奥秘的距离,常用于需要按照网格布局移动的场景,例如无人驾驶出租车行驶、物流配送等.在算法设计中,曼哈顿距离也常用于图像处理和路径规划等问题.曼哈顿距离用于标明两个点在空间(平面)直角坐标系上的绝对轴距总和.例如在平面直角坐标系内有两个点它们之间的曼哈顿距离(1)、已知点 , 求的值;(2)、已知平面直角坐标系内一定点 , 动点满足 , 求动点围成的图形的面积:(3)、已知空间直角坐标系内一定点 , 动点满足 , 若动点围成的几何体的体积是 , 求的值.
-
5、如图,在四棱锥中,平面平面 , 且 .
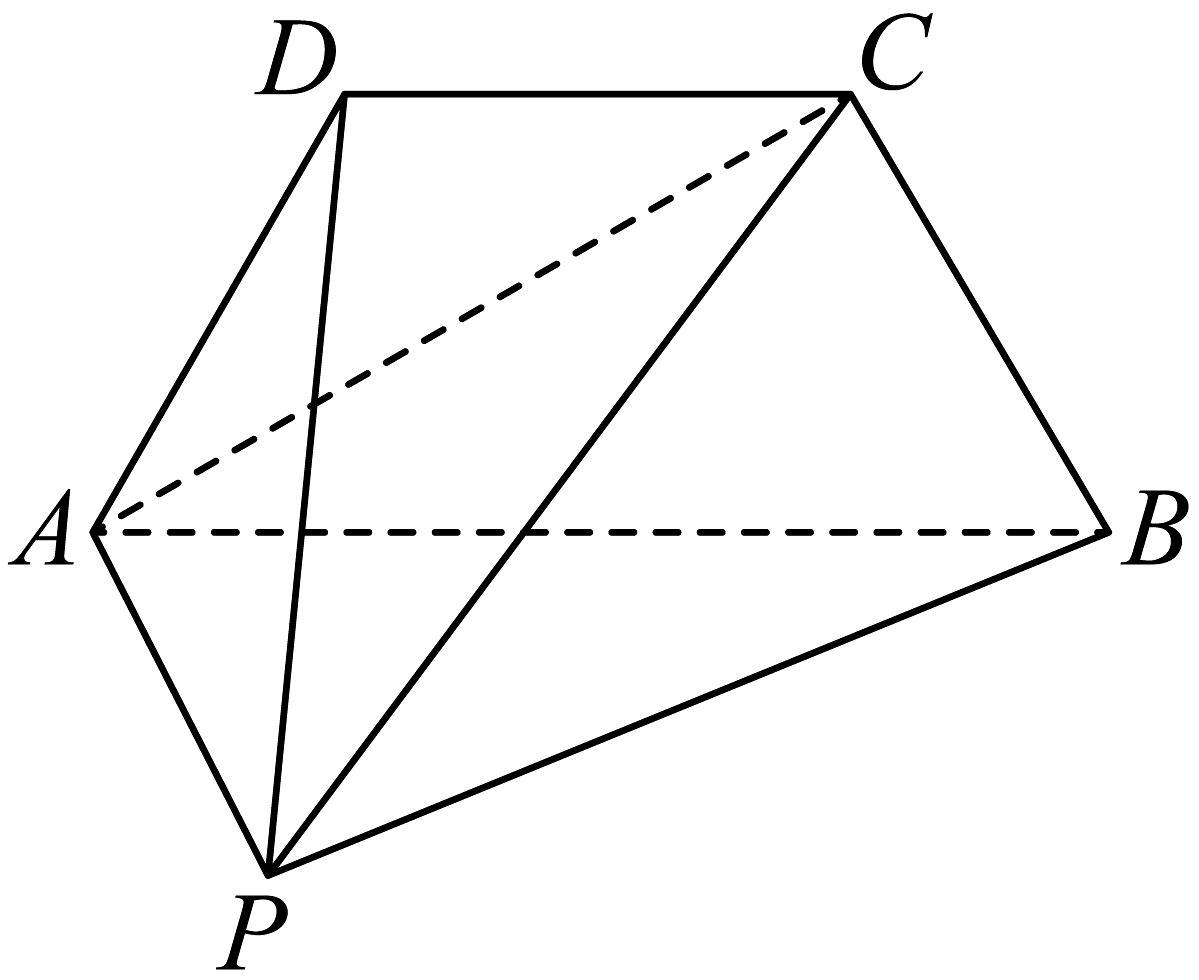 (1)、证明:平面平面;(2)、求平面与平面夹角的正弦值.
(1)、证明:平面平面;(2)、求平面与平面夹角的正弦值. -
6、已知函数 , 若 , 都有成立,则的取值范围为( )A、 B、 C、 D、
-
7、下列说法正确的是( )A、“”是“直线与直线互相垂直”的充要条件 B、“”是“直线与直线互相平行”的充要条件 C、直线的倾斜角的取值范围是 D、若点 , , 直线过点且与线段相交,则的斜率的取值范围是
-
8、正实数 , 满足 , 则的最小值为 .
-
9、如图,四棱台中,上、下底面均是正方形,且侧面是全等的等腰梯形, , 分别为的中点,上下底面中心的连线垂直于上下底面,且与侧棱所在直线所成的角为.
 (1)、求证:∥平面;(2)、求点到平面的距离;(3)、边上是否存在点 , 使得直线与平面所成的角的正弦值为 , 若存在,求出线段的长;若不存在,请说明理由
(1)、求证:∥平面;(2)、求点到平面的距离;(3)、边上是否存在点 , 使得直线与平面所成的角的正弦值为 , 若存在,求出线段的长;若不存在,请说明理由 -
10、《中国制造2025》是中国实施制造强国战略第一个十年的行动纲领,制造业是国民经济的主体,是立国之本、兴国之器、强国之基.发展制造业的基本方针为质量为先,坚持把质量作为建设制造强国的生命线某电子产品制造企业为了提升生产效率,对现有的一条电子产品生产线进行技术升级改造,为了分析改造的效果,该企业质检人员从该条生产线所生产的电子产品中随机抽取了1000件,检测产品的某项质量指标值,根据检测数据得到下表(单位:件).
质量指标值
产品
60
100
160
300
200
100
80
(1)、估计这组样本的质量指标值的平均数和方差(同一组中的数据用该组区间中点值作代表);(2)、设表示不大于x的最大整数,表示不小于x的最小整数,s精确到个位, , , , 根据检验标准,技术升级改造后,若质量指标值有落在内,则可以判断技术改造后的产品质量初级稳定;若有落在内,则可以判断技术改造后的产品质量稳定,可认为生产线技术改造成功.请问:根据样本数据估计,是否可以判定生产线的技术改造是成功的? -
11、已知是边长为2的正方体,点E为的中点,点F为的中点.
 (1)、求证:;(2)、求平面EFC与平面BFC夹角的余弦值.(3)、求点到直线的距离.
(1)、求证:;(2)、求平面EFC与平面BFC夹角的余弦值.(3)、求点到直线的距离. -
12、在平面直角坐标系中,是坐标原点,直线的方程为 ,(1)、若 , 求过点且与直线平行的直线方程;(2)、已知原点到直线的距离为4,求的值;(3)、已知直线在两条坐标轴上截得的截距相等,求的值.
-
13、A,B,C三人参加知识闯关比赛,三人闯关成功与否相互独立.已知A闯关成功的概率是 , A,B,C三人闯关都成功的概率是 , A,B,C三人闯关都不成功的概率是 .(1)、求B,C两人各自闯关成功的概率;(2)、求A,B,C三人中恰有两人闯关成功的概率;(3)、求A,B,C三人中至少一人闯关成功的概率.
-
14、在棱长为1的正方体中,为底面的中心,是棱上一点,且 , , 为线段的中点,给出下列命题:

①四点共面;
②三棱锥的体积与的取值有关;
③当时,;
④当时,过三点的平面截正方体所得截面的面积为.
其中正确的有(填写序号).
-
15、数据3.2,3.6,4.5,2.4,4.6,6.4,7.8,7.9,8.0,8.1,8.4,8.6的上四分位数是 .
-
16、已知直线经过 , 则该直线过定点 .
-
17、直线的方程为 , 若在x轴上的截距为 , 且 . 则下列说法正确的是( )A、直线与的交点坐标为 , 直线在y轴上的截距是 B、已知直线经过与的交点,且在y轴上的截距是在x轴上的截距的2倍,的方程为 C、已知动直线经过与的交点,当原点到距离最大时,到距离为 D、直线 , , 若 , 则或2
-
18、在四面体中,下列说法正确的有( )A、若 , 则 B、若Q为的重心,则 C、若 , , 则 D、若四面体的各棱长都为2,M,N分别为PA,BC的中点,则 .
-
19、如图,在直三棱柱中, , 则与所成的角的余弦值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
20、设点 , 直线过点 , 且与线段相交,则直线的斜率取值范围是( )A、 B、 C、 D、