相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
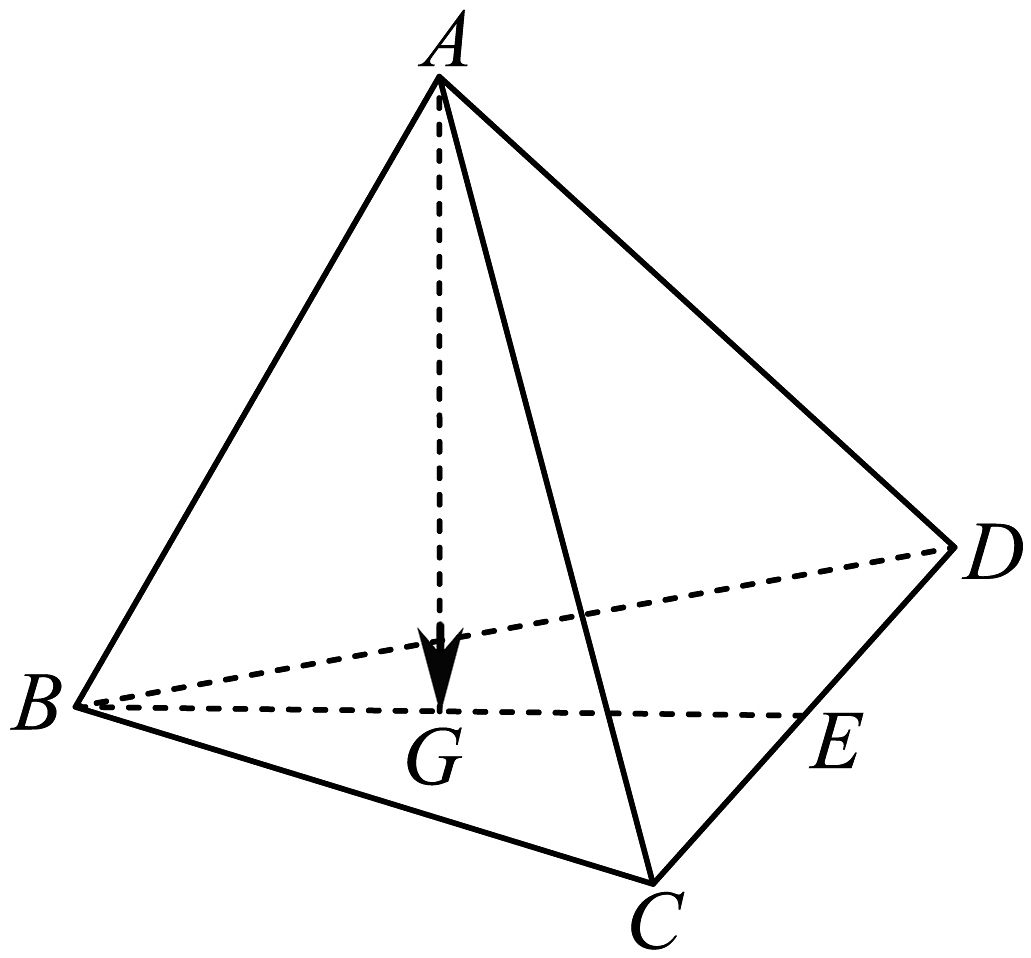
1、在四面体中,、分别是、的中点,若 , 则 .
-
2、已知P(A)=0.4,P(B)=0.2.(1)如果B⊆A,则P(A∪B)= , P(AB)=;(2)如果A,B互斥,则P(A∪B)= , P(AB)=.
-
3、如图,正方体的棱长为1,E,F,G分别为的中点,则下列说法正确的是( )
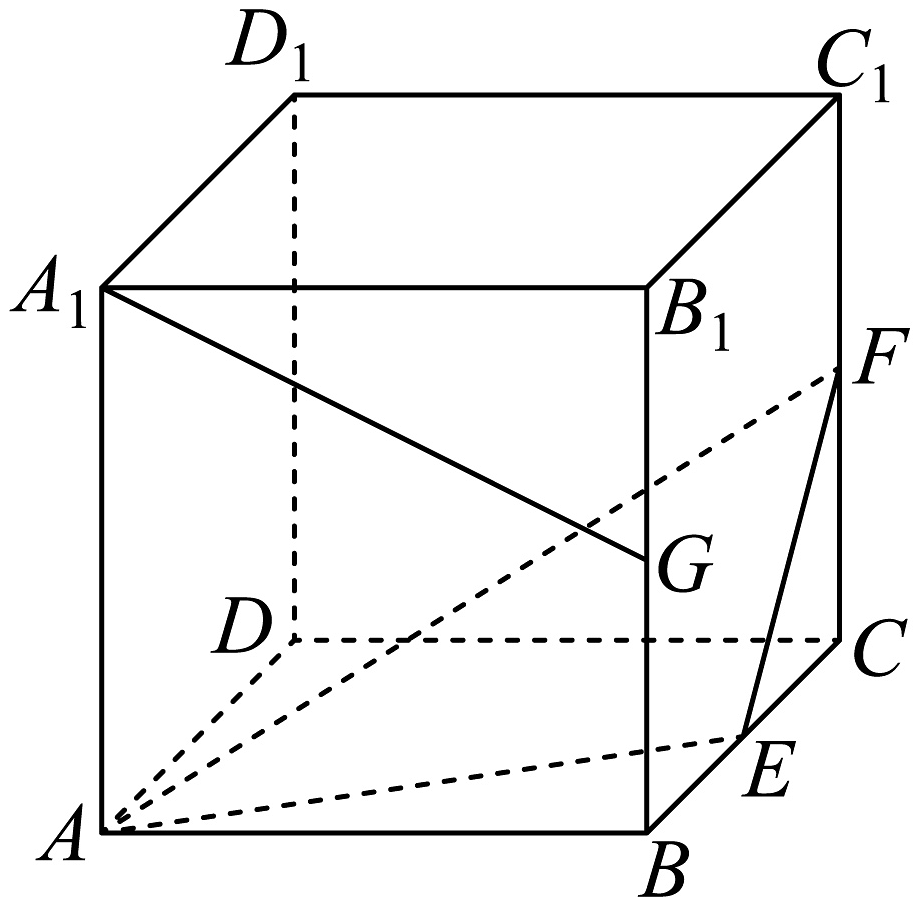 A、直线与直线垂直 B、直线与平面平行 C、平面截正方体所得的截面面积为 D、点C与点G到平面的距离相等
A、直线与直线垂直 B、直线与平面平行 C、平面截正方体所得的截面面积为 D、点C与点G到平面的距离相等 -
4、下列说法中,正确的是( )A、概率是频率的稳定值,频率是概率的近似值 B、做次随机试验,事件发生次,则事件发生的频率就是事件的概率 C、频率是不能脱离次试验的试验值,而概率是具有确定性的不依赖于试验次数的理论值 D、任意事件发生的概率总满足
-
5、如图,在棱长为的正方体中,点是平面内一个动点,且满足 , 则直线与直线所成角的取值范围为( )(参考数据:)
 A、 B、 C、 D、
A、 B、 C、 D、 -
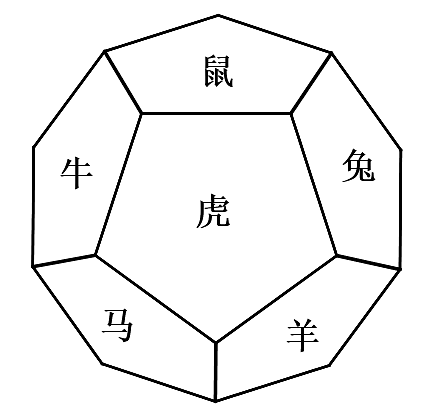
6、中国古代传统文化中,有记录人们出生年份的属相记录法,共有12种属相,分别是鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪,也称子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.现有一个正十二面体,每一个(正五边形)面标有一个属相,如图.现将这个质地均匀的正十二面体先后抛掷两次,则朝上的面两次属相不同的概率是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、若向量与向量互相垂直,则的值为( )A、1 B、2 C、3 D、4
-
8、在长方体中,为与的交点.若 , , , 则下列向量中与相等的向量是( )A、 B、 C、 D、
-
9、甲、乙两个同学下棋,若甲获胜的概率为0.2,甲不输的概率为0.7,则甲、乙下成和棋的概率为( )A、0.5 B、0.7 C、0.9 D、0.4
-
10、已知向量 , 则( )A、 B、3 C、9 D、0
-
11、一个家庭中先后有两个小孩,则他(她)们的性别情况可能为( )A、男女、男男、女女 B、男女、女男 C、男男、男女、女男、女女 D、男男、女女
-
12、对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设A={两次都击中飞机},B={两次都没击中飞机},C={恰有一弹击中飞机},D={至少有一弹击中飞机},下列关系不正确的是( )A、 B、 C、 D、
-
13、已知 , 且( )A、B B、 C、 D、
-
14、黎曼猜想是解析数论里的一个重要猜想,它被很多数学家视为是最重要的数学猜想之一.它与函数(为常数)密切相关,请解决下列问题:(1)、当时,求在点处的切线方程;(2)、当时,证明有唯一极值点.
-
15、如图,在三棱锥中,底面为上一点,且平面平面 , 三棱锥的体积为.
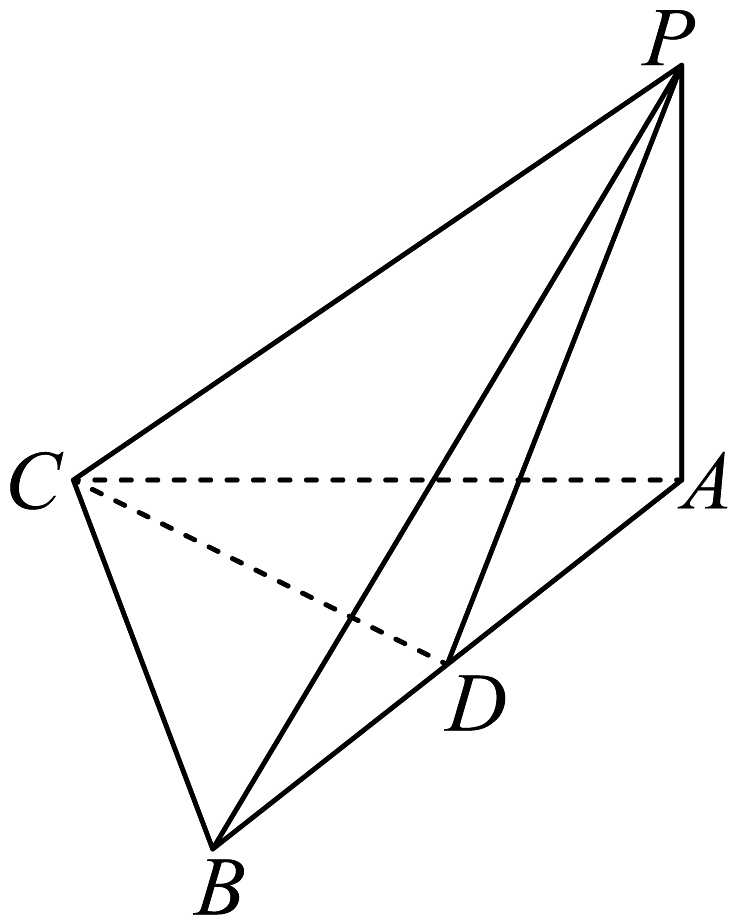 (1)、求证:为的中点;(2)、求直线与平面所成角的正弦值.
(1)、求证:为的中点;(2)、求直线与平面所成角的正弦值. -
16、一款便携式行李箱的密码是由数字1,2,3组成的一个五位数,这三个数字的每个数字在密码中至少出现一次,且它们出现的概率相等.(1)、求该款行李箱密码的不同种数;(2)、记X表示该款行李箱密码中数字1出现的次数,求X的分布列和数学期望.
-
17、在△中,角的对边分别为 , 已知(1)、求 ;(2)、若 分别为边 上的中点,为 的重心,求 的余弦值.
-
18、若 , 则 .
-
19、已知等差数列的首项 , 公差 , 求第10项的值为.
-
20、已知函数是定义在R上的奇函数,且 , 则 .