版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，E为棱 $A_{1} C_{1}$ 的中点.设 $\vec{B A} = \vec{a}$ ， $\vec{B B_{1}} = \vec{b}$ ， $\vec{B C} = \vec{c}$ ，则 $\vec{B E} =$ （）

A、 $\frac{1}{2} \vec{a} + \vec{b} + \frac{1}{2} \vec{c}$ B、 $\frac{1}{2} \vec{a} + \frac{1}{2} \vec{b} + \vec{c}$ C、 $\vec{a} + \frac{1}{2} \vec{b} + \frac{1}{2} \vec{c}$ D、 $\frac{1}{2} \vec{a} + \vec{b} + \vec{c}$

查看解析
2、若方程 $\frac{x^{2}}{6 - m} + \frac{y^{2}}{m - 4} = 1$ 表示焦点在 $y$ 轴上的椭圆，则实数 $m$ 的取值范围是（）

A、 $4 < m < 6$ B、 $m > 5$ C、 $4 < m < 5$ D、 $5 < m < 6$

查看解析
3、已知直线 $l_{1} : (m - 6) x + (4 - m) y + 1 = 0$ 与直线 $l_{2} : x + m y + 1 = 0$ 垂直，则 $m$ 的值为（）

A、1或 $- 4$ B、1或4 C、2或 $- 3$ D、2或3

查看解析
4、已知直线的一个方向向量为 $(3, - \sqrt{3})$ ，则该直线的倾斜角是（）

A、 $45 °$ B、 $120 °$ C、 $135 °$ D、 $150 °$

查看解析
5、已知空间向量 $\vec{a} = (x, 1, 2)$ ， $\vec{b} = (4, 2, 4)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $x =$ （）

A、1 B、 $- \frac{5}{2}$ C、 $- \frac{3}{2}$ D、3

查看解析
6、 $2023$ 年， $8$ 月 $29$ 日，华为 $Mate60Pro$ 在华为商城正式上线，成为全球首款支持卫星通话的大众智能手机.其实在 $2019$ 年 $5$ 月 $19$ 日，华为被美国列入实体名单，以所谓科技网络安全为借口，对华为施加多轮制裁.为了进一步增加市场竞争力，华为公司计划在 $2020$ 年利用新技术生产某款新手机，通过市场分析，生产此款手机全年需投入固定成本 $300$ 万，每生产 $x ($ 千部 $)$ 手机，需另投入成本 $R (x)$ 万元，且 $R (x) = \{\begin{array}{l} 10 x^{2} + 100 x ， 0 < x < 50 \\ 701 x + \frac{10000}{x} - 9450 ， x \geq 50 \end{array}$ 由市场调研知此款手机售价 $0.7$ 万元，且每年内生产的手机当年能全部销售完.

(1)、求出 $2020$ 年的利润 $w (x) ($ 万元 $)$ 关于年产量 $x ($ 千部 $)$ 的表达式 $;$

(2)、 $2020$ 年年产量为多少 $($ 千部 $)$ 时，企业所获利润最大 $?$ 最大利润是多少 $?$

查看解析
7、已知偶函数 $f (x)$ 和奇函数 $g (x)$ 的定义域均为 $R$ ，且 $f (x) - g (x) = 2^{1 - x}$ ．

(1)、求函数 $f (x)$ 和 $g (x)$ 的解析式；

(2)、若 $\forall x \in R$ ，不等式 $m f (x) \leq {[g (x)]}^{2} + 2 m + 9$ 恒成立，求实数 $m$ 的取值范围．

查看解析
8、已知 $a^{\frac{1}{2}} + a^{- \frac{1}{2}} = 3, a > 1$ ，求下列各式的值：

(1)、 $\frac{a^{2} + a^{- 2} - 1}{a + a^{- 1} - 1}$ ；

(2)、 $\frac{(a^{2} + 1) (a^{- \frac{2}{3}} - a^{- \frac{1}{2}})}{\sqrt{a^{\frac{2}{3}} + a - 2 a^{\frac{5}{6}}}}$ ．

查看解析
9、对于函数 $f (x)$ ，如果存在函数 $g (x) = a x + b (a$ ， $b$ 为常数），使得对于区间 $D$ 上的一切实数 $x$ 都有 $f (x) \leq g (x)$ 成立，则称函数 $g (x)$ 为函数 $f (x)$ 在区间 $D$ 上的一个“覆盖函数”，设 $f (x) = 2^{x}$ ， $g (x) = 2 x$ ，若函数 $g (x)$ 为函数 $f (x)$ 在区间 $[m, n]$ 上的一个“覆盖函数”，则 $2^{| m - n |}$ 的最大值为．

查看解析
10、若 $x^{2} - 3 x + 1 = 0$ ，则 $x^{3} + \frac{1}{x^{3}}$ 的值为.

查看解析
11、若 $a = 27, b = 16$ ， $\frac{(- 2 \sqrt{a b}) \times (- 8 \sqrt[3]{a^{2} b^{5}})}{\sqrt[6]{a^{2} b^{7}} \times 4 \sqrt[4]{a^{2} b^{5}}}$ =

查看解析
12、 ${(5 \frac{1}{16})}^{0.5} - {(2 \frac{10}{27})}^{- \frac{2}{3}} - {(2^{- 1})}^{{(\sqrt{3})}^{2}}$ 的值是

查看解析
13、已知函数 $f (x)$ 满足：① $\forall x$ ， $y \in R$ ， $f (x y) = {[f (x)]}^{y}$ ；② $f (- 2) > 1$ ，则（）

A、 $f (0) = 0$ B、 $f (x + y) = f (x) \cdot f (y)$ C、 $f (x)$ 在 $R$ 上是减函数 D、 $\forall x \in [1, 3]$ ， $f (x^{2} - k x) \cdot f (x - 3) \geq 1$ ，则 $k \geq 3$

查看解析
14、已知函数 $f (x) = 2^{x} - 2^{- x}$ ，若 $x_{1} < 0, x_{1} + x_{2} > 0$ ，则（）

A、 $f (x_{1}) - f (- x_{2}) > 0$ B、 $f (x_{1}) - f (- x_{2}) < 0$ C、 $f (x_{1}) + f (x_{2}) > 0$ D、 $f (x_{1}) + f (x_{2}) < 0$

查看解析
15、下列结论中，不正确的是（）

A、 ${0.2}^{0.2} > {0.3}^{0.2}$ B、 $2^{- \frac{1}{3}} < 3^{- \frac{1}{3}}$ C、 ${0.8}^{- 0.1} > {1.25}^{0.2}$ D、 ${1.7}^{0.3} > {0.9}^{3.1}$

查看解析
16、 $⌈x⌉$ 表示大于或者等于 $x$ 的最小整数， $⌊x⌋$ 表示小于或者等于 $x$ 的最大整数．已知函数 $f (x) = \{\begin{matrix} ⌈x^{2} + 3 a x + a⌉, & x \leq 0 \\ e^{- x}, & x > 0 \end{matrix}$ ，且 $f (x)$ 满足：对 $\forall x_{1}, x_{2} \in R$ 有 $(x_{1} - x_{2}) (f (x_{1}) - f (x_{2})) \leq 0$ ，则 $a$ 的可能取值是（）

A、 $- \frac{1}{9}$ B、0 C、 $\frac{1}{3}$ D、 $\frac{4}{9}$

查看解析
17、已知奇函数 $f (x) = a^{x} - b \cdot a^{- x} (a > 0, a \neq 1)$ 在 $[- 1, 1]$ 上的最大值为 $\frac{8}{3}$ ，则 $a =$ （）

A、 $\frac{1}{3}$ 或3 B、 $\frac{1}{2}$ 或2 C、3 D、2

查看解析
18、设 $a = {(\frac{2}{3})}^{\frac{1}{3}}$ ， $b = {1.5}^{- 0.2}$ ， $c = {0.8}^{0.2}$ ，则（）

A、 $a < c < b$ B、 $c < a < b$ C、 $b < c < a$ D、 $a < b < c$

查看解析
19、已知指数函数 $y = {(\frac{b}{a})}^{x}$ 的图象如图所示，则一次函数 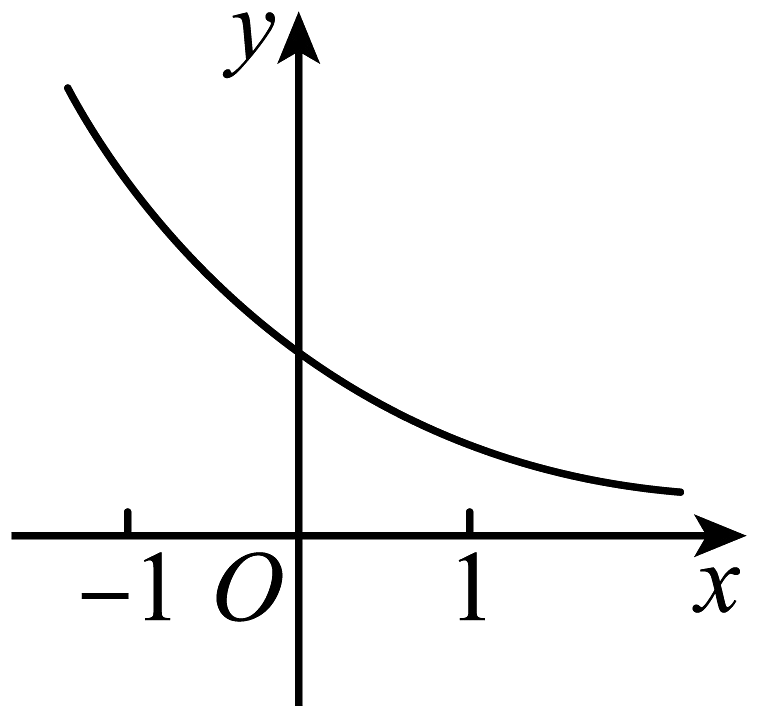$y = a x + b$ 的图象可能是（       ）


A、    B、    C、    D、

查看解析
20、已知函数 $f (x) = \frac{2^{x} - 1}{2^{x} + 1} + a x^{2023} - \frac{b}{x} - 6$ ， $f (- 2023) = 5$ ，则 $f (2023) =$ （）

A、12 B、 $- 12$ C、 $- 17$ D、17

查看解析

上一页 855 856 857 858 859 下一页跳转