相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、数列中,从第二项起,每一项与其前一项的差组成的数列称为的一阶差数列,记为 , 依此类推,的一阶差数列称为的二阶差数列,记为 , ….如果一个数列的p阶差数列是等比数列,则称数列为p阶等比数列 .(1)、已知数列满足 , .
(ⅰ)求 , , ;
(ⅱ)证明:是一阶等比数列;
(2)、已知数列为二阶等比数列,其前5项分别为 , 求及满足为整数的所有n值. -
2、已知函数在区间上是单调函数,(1)、求实数m的所有取值组成的集合A;(2)、试写出在区间上的最大值;(3)、设 , 令 , 若关于m的方程恰有两个不相等的实数根,求实数a的取值范围.
-
3、第19届亚运会于2023年9月23日至10月8日在杭州举行,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估.该商品原来每件售价为25元,年销售8万件.(1)、据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?(2)、为了抓住此次契机,扩大该商品的影响力,提高年销售量,公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到元.公司拟投入万元作为技改费用,投入50万元作为固定宣传费用,投入万元作为浮动宣传费用.试问:当该商品改革后的销售量至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
-
4、已知集合 , .(1)、当时,求 , ;(2)、若 , 求实数的取值范围.
-
5、(1)计算
(2)计算(式中字母均是正数).
-
6、如图所示,杭师大附中校园里有一块矩形空地 , 要在这块空地上开辟一个内接四边形绿地(图中四边形),使其四个顶点分别落在矩形的四条边上已知 , 且 , 设 , 绿地面积为 , 若 , 则绿地面积的最大值为 . (用含的式子作答)

-
7、若两个正实数 , 满足 , 则的最小值为 .
-
8、游客从杭州城站到西湖之滨,最先看到的是公园濒湖一带的护栏,南北绵延约1公里,柱与柱之间是一条条轻匀悬链,映照湖上的水光山色.德国数学家莱布尼兹把这种架在等高两柱间,自然下垂有均匀密度的曲线称为悬链线.如果建立适当的平面直角坐标系,那么悬链线可以表示为函数 , 其中 , 则下列关于悬链线函数的性质判断中,正确的有( )A、为奇函数 B、为偶函数 C、的最小值为a D、的单调增区间为
-
9、已知关于x的不等式的解集为或 , 则下列说法正确的是( )A、 B、不等式的解集为 C、不等式的解集为或 D、
-
10、下列说法中正确的是( )A、若函数是R上的奇函数,则 B、函数的图象与y轴最多有一个交点 C、若是一次函数,满足 , 则 D、式子化简的结果为7
-
11、已知函数 , 且 , 则的取值范围为( )A、 B、 C、 D、
-
12、函数的图象大致为( )A、
 B、
B、 C、
C、 D、
D、
-
13、已知函数是偶函数,则的单调增区间是( )A、 B、 C、 D、
-
14、三棱柱中,侧面为菱形, , , , .
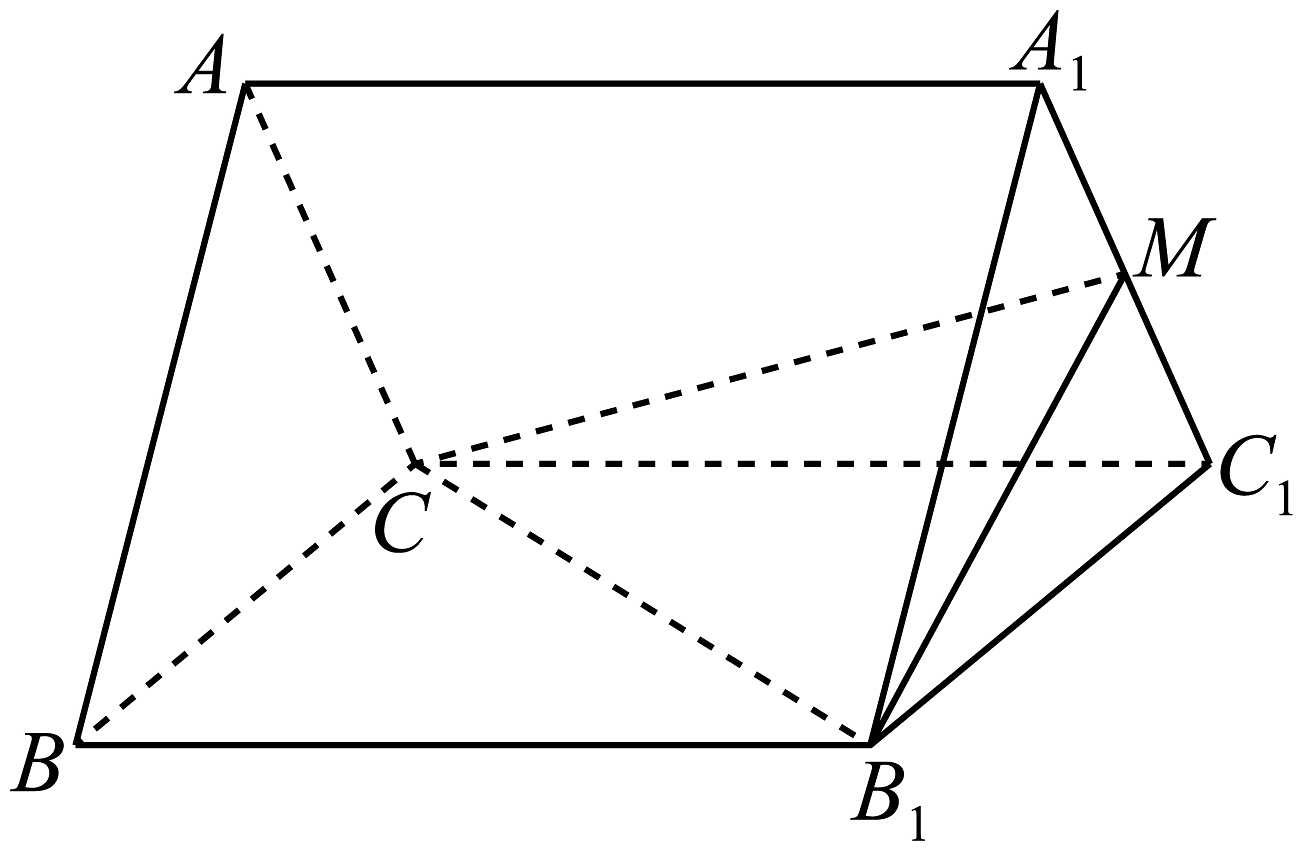
(1)求证:面面;
(2)在线段上是否存在一点M,使得二面角为 , 若存在,求出的值,若不存在,请说明理由.
-
15、已知 , 二次函数 .(1)、当时,求在上的最大值;(2)、设不等式的解集为A,又知集合 . 若 , 求a的取值范围.
-
16、已知函数 .(1)、试用函数单调性定义证明函数在R上单调递增;(2)、求不等式的解集.
-
17、已知区间 .
(1)若 , 求实数a的值;
(2)若 , 求实数a的取值范围.
-
18、(1)求值:;
(2)已知 , 求的值.
-
19、①在上单调递增,② , 则满足上述两个条件的函数为(写出一个即可);
-
20、已知幂函数的图像经过点 , 则这个函数的解析式为=