版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、函数 $f (x) = \sqrt{2} sin (ω x + φ) (0 < ω \leq 2, - \frac{π}{2} < φ < \frac{π}{2})$ 的部分图象如图所示，则下列说法中正确的是（）

A、 $φ = - \frac{π}{4}$ B、 $f (x)$ 的表达式可以写成 $f (x) = \sqrt{2} cos (2 x + \frac{π}{4})$ C、 $f (x)$ 的图象向左平移 $\frac{3 π}{8}$ 个单位长度后得到的新函数是偶函数 D、若方程 $f (x) = 1$ 在 $(0, m)$ 上有且只有6个根，则 $m \in (\frac{5 π}{2}, \frac{13 π}{4}]$

查看解析
2、已知 $α$ ， $β$ 为两个不同的平面， $a$ ， $b$ 为两条不同的直线，A为点，下列说法不正确的是（）

A、 $α // β, a \subset α, b \subset β \Rightarrow a // b$ B、 $a \subset α, b \cap α = A \Rightarrow a, b$ 为异面直线 C、 $a // b, a // α, b ⊄ α \Rightarrow b // α$ D、 $b // α, a \subset α \Rightarrow a // b$

查看解析
3、在 $△ A B C$ 中，内角 $A, B, C$ 的对边分别为 $a, b, c$ ，且 $S_{△ A B C} = \frac{\sqrt{3}}{4} b^{2}$ ，则 $\frac{a^{2} + c^{2}}{a c}$ 的最大值为（）

A、2 B、4 C、 $\frac{4 \sqrt{3}}{3}$ D、 $4 \sqrt{3}$

查看解析
4、若函数 $f (x) = ln [(a - 1) x + 1]$ 在 $(2, 3)$ 上单调递减，则实数 $a$ 的取值范围是（）

A、 $(- \infty, 1)$ B、 $[\frac{2}{3}, 1)$ C、 $[\frac{1}{2}, 1)$ D、 $(\frac{2}{3}, 1)$

查看解析
5、已知向量 $\vec{a} = (1, 2), \vec{b} = (- 3, t)$ ，且 $\vec{a} / / \vec{b}$ ，则 $|\vec{a} + \vec{b}| =$ （）

A、 $\sqrt{2}$ B、 $\sqrt{5}$ C、 $\sqrt{10}$ D、 $2 \sqrt{5}$

查看解析
6、 $△ A B C$ 的直观图 $△ A^{'} B^{'} C^{'}$ 如图所示，其中 $A^{'} B^{'} / / x^{'}$ 轴， $A^{'} C^{'} / / y^{'}$ 轴，且 $A^{'} B^{'} = A^{'} C^{'} = 2$ ，则 $△ A B C$ 的面积为（）

A、 $2 \sqrt{2}$ B、2 C、4 D、 $4 \sqrt{2}$

查看解析
7、若 $a \in R$ ，则“ $a = 3$ ”是“ $(a + 1) (a - 3) = 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看解析
8、已知复数 $z$ 满足 $(1 + i) z = 1 - 2 i$ ，其中 $i$ 为虚数单位，则 $z =$ （）

A、 $3 - i$ B、 $3 + i$ C、 $- \frac{1}{2} + \frac{3}{2} i$ D、 $- \frac{1}{2} - \frac{3}{2} i$

查看解析
9、设等比数列 $\{a_{n}\}$ 的前 $n$ 项和为 $S_{n}$ ，且 $a_{5} a_{7} = 3, a_{3} a_{10} = 9$ ，则 $\frac{S_{10}}{S_{5}} =$ （）

A、243 B、244 C、81 D、82

查看解析
10、根据某地区气象水文部门长期统计，可知该地区每年夏季有小洪水的概率为0.25，有大洪水的概率为0.05.
（1）从该地区抽取的 $n$ 年水文资料中发现，恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等，求 $n$ 的值；
（2）今年夏季该地区某工地有许多大型设备，遇到大洪水时要损失60000元，遇到小洪水时要损失20000元.为保护设备，有以下3种方案：
方案1：修建保护围墙，建设费为3000元，但围墙只能防小洪水.
方案2：修建保护大坝，建设费为7000元，能够防大洪水.
方案3：不采取措施.
试比较哪一种方案好，请说明理由.

查看解析
11、在如图所示的试验装置中，两个正方形框架ABCD，ABEF的边长都是1，且它们所在的平面互相垂直．活动弹子M，N分别在正方形对角线AC和BF上移动，且CM和BN的长度保持相等，记 $C M = B N = a$ $(0 < a < \sqrt{2})$ ．

(1)、求MN的长；

(2)、当MN的长最小时，求平面MNA与平面MNB夹角的余弦值．

查看解析
12、已知动点 $M (x, y)$ 与定点 $F (4, 0)$ 的距离和M到定直线 $l : x = \frac{25}{4}$ 的距离的比是常数 $\frac{4}{5}$ ．

(1)、求动点M的轨迹E；

(2)、在E上是否存在一点使得它到直线 $4 x - 5 y + 40 = 0$ 的距离最小？若存在，请求出最小距离；若不存在，请说明理由．

查看解析
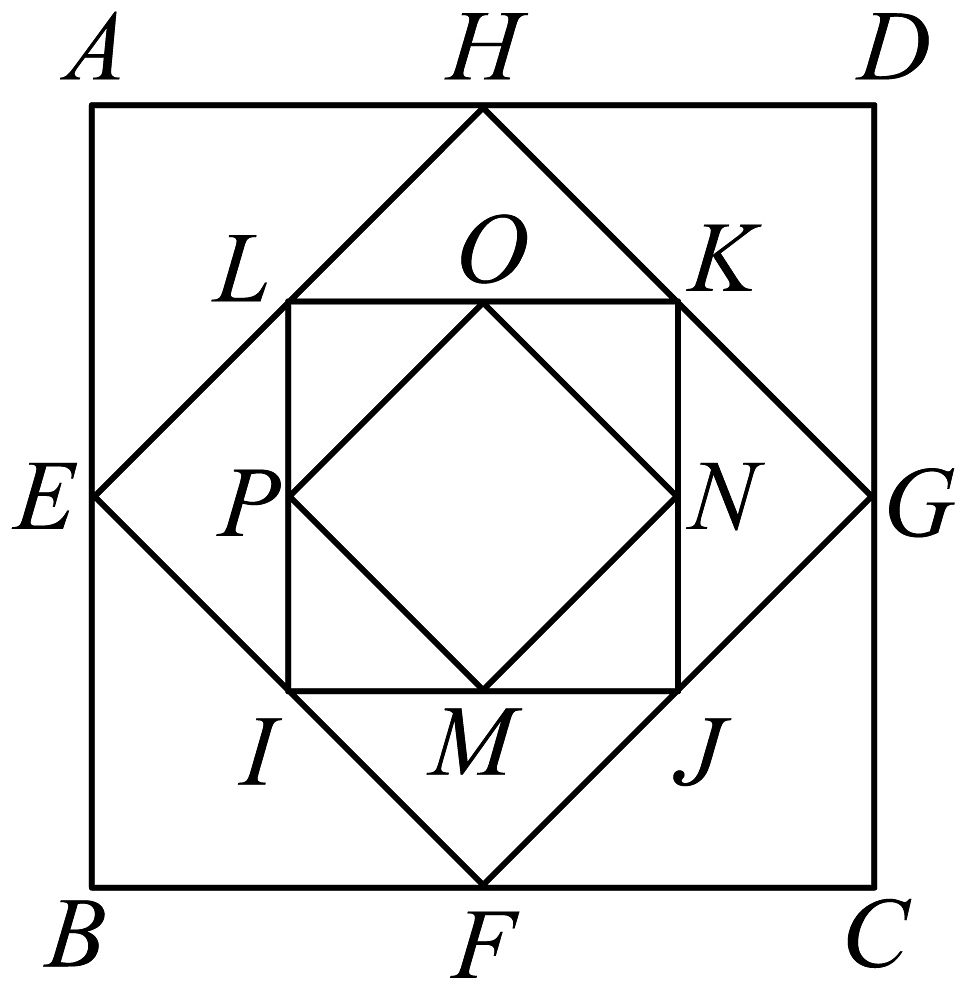
13、如图，正方形ABCD的边长为5，取正方形ABCD各边的中点E，F，G，H，作第二个正方形EFGH，然后再取正方形EFGH各边的中点I，J，K，L，作第三个正方形IJKL，依次方法一直继续下去，则所有这些正方形的面积之和趋近于．

查看解析
14、已知 $O$ 为坐标原点，直线 $y = x - 2$ 与抛物线 $y^{2} = 2 x$ 相交于 $A, B$ 两点，则 $△ A O B$ 的面积为．

查看解析
15、若平面向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 两两的夹角相等，且 $|\vec{a}| = |\vec{b}| = 1$ ， $|\vec{c}| = 3$ ，则 $|\vec{a} + \vec{b} + \vec{c}| =$ .

查看解析
16、已知A，B为双曲线 $x^{2} - y^{2} = 1$ 上不同两点，下列点中可为线段 $A B$ 的中点的是（）

A、 $(1, 1)$ B、 $(2, 3)$ C、 $(\sqrt{2}, 1)$ D、 $(- 1, \frac{1}{2})$

查看解析
17、考虑以 $Ω$ 为样本空间的古典概型．设X和Y定义 $Ω$ 上，取值 ${0, 1}$ 的成对分类变量，则“ ${X = 0}$ 与 ${Y = 0}$ 独立”是“ ${X = 1}$ 与 ${Y = 1}$ 独立”的（）

A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件

查看解析
18、空间中有8个点，其中任何4个点不共面，过每3个点作一个平面，可以作的平面个数为（）

A、42 B、56 C、64 D、81

查看解析
19、已知集合 $A = \{x \in Q |(x - 2) (x^{2} - 3) = 0\}$ ， $B = \{x |0 \leq x \leq 2\}$ ，则 $A \cap B =$ （）

A、 ${2, \sqrt{3}, - \sqrt{3}}$ B、 ${2, \sqrt{3}}$ C、 ${2}$ D、 $\emptyset$

查看解析
20、已知函数 $f (x) = - cos x$ ， $g (x) = \frac{x^{2}}{2} - 1$ ， $x \in [0, + \infty)$ .

(1)、判断 $g (x) \geq f (x)$ 是否对 $\forall x \in [0, + \infty)$ 恒成立，并给出理由；

(2)、证明：
①当 $0 < m < n < \frac{π}{2}$ 时， $\frac{sin m - sin n}{m - n} > cos n$ ；
②当 $a_{i} = \frac{1}{2^{i}} (i \in N^{*})$ ， $k_{i} = \frac{f^{'} (a_{i + 1}) - f^{'} (a_{i})}{a_{i + 1} - a_{i}} (i = 1 ， 2 ， \dots ， n - 1)$ 时， $\sum_{i = 1}^{n - 1} k_{i} > \frac{6 n - 7}{6}$ .

查看解析

上一页 614 615 616 617 618 下一页跳转