相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、样本数据的极差和第75百分位数分别为 .
-
2、已知定义在上且不恒为的函数对任意 , 有 , 且的图象是一条连续不断的曲线,则( )A、的图象存在对称轴 B、的图象有且仅有一个对称中心 C、是单调函数 D、为一次函数且表达式不唯一
-
3、已知正数满足 , 则( )A、 B、 C、 D、
-
4、设曲线 , 过点的直线与交于两点,线段的垂直平分线分别交直线和于点 , 若 , 则的斜率可以为( )A、 B、 C、2 D、
-
5、在四面体中, , 且四面体的各个顶点均在球的表面上,则球的体积为( )A、 B、 C、 D、
-
6、在中,为边上靠近点的三等分点,为线段(含端点)上一动点,若 , 则( )A、 B、 C、 D、
-
7、已知 , 则( )A、 B、 C、 D、
-
8、已知 , 则( )A、 B、 C、 D、
-
9、已知集合 , 则( )A、 B、 C、 D、
-
10、如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,则下列结论正确的是( )
 A、圆柱的侧面积为 B、圆锥的侧面积为 C、圆柱的侧面积与球的表面积相等 D、圆柱、圆锥、球的体积之比为
A、圆柱的侧面积为 B、圆锥的侧面积为 C、圆柱的侧面积与球的表面积相等 D、圆柱、圆锥、球的体积之比为 -
11、定义在上的函数满足以下条件:① , ②对任意 , 当时都有 , 则 , , 的大小关系是( )A、 B、 C、 D、
-
12、下列图形中,可以表示函数的是( )A、
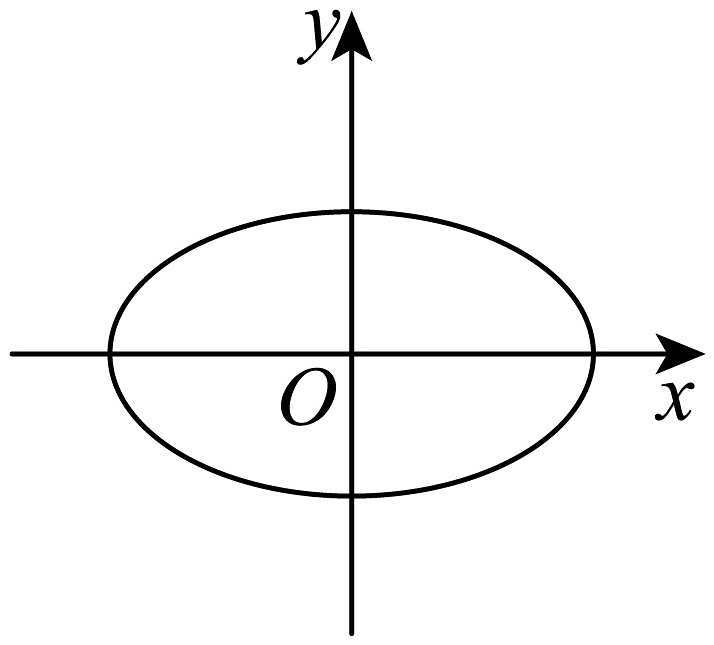 B、
B、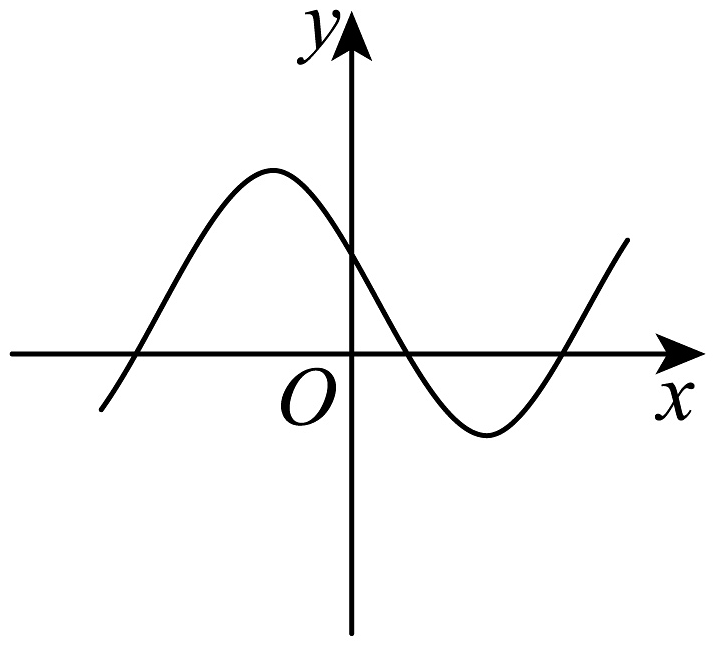 C、
C、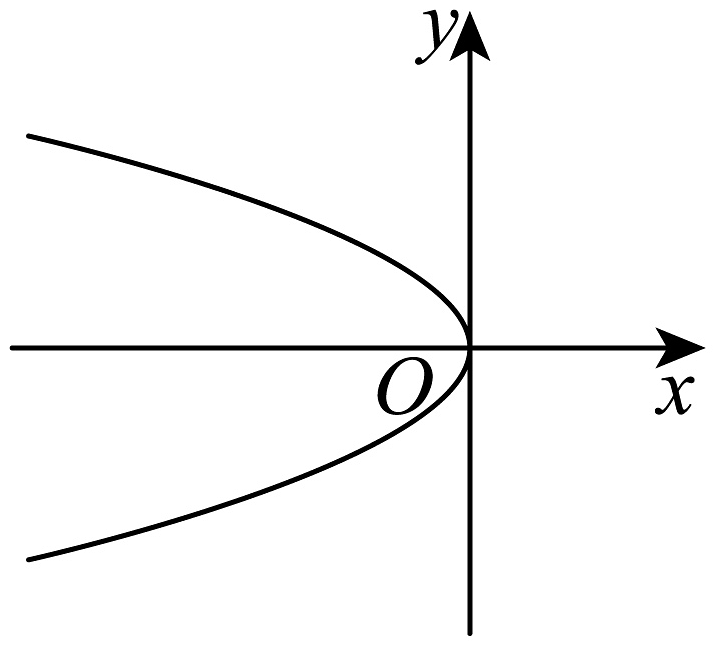 D、
D、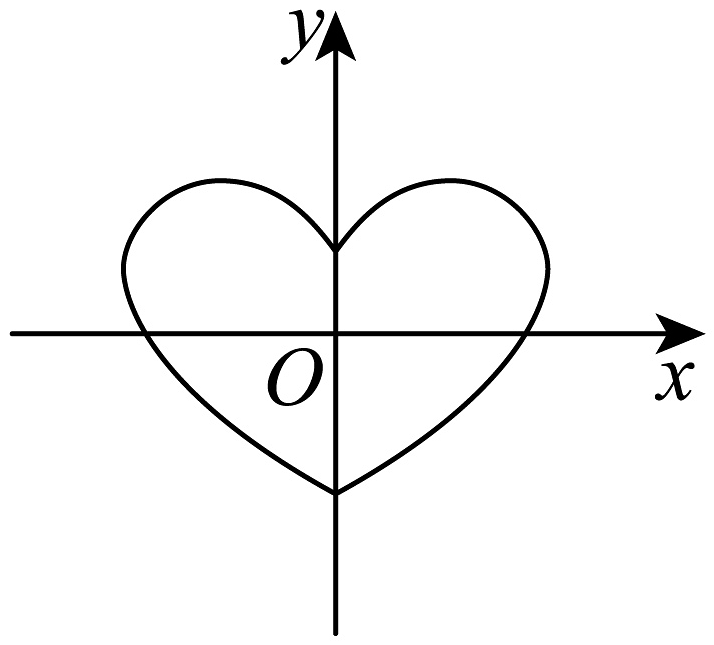
-
13、在数列中, , 其前n项和为 , 且(且).(1)、求的通项公式;(2)、设数列满足 , 其前项和为 , 若恒成立,求实数的取值范围.
-
14、已知函数和的定义域分别为和 , 若对任意 , 恰好存在个不同的实数 , 使得(其中),则称为的“重覆盖函数”.(1)、试判断是否为的“2重覆盖函数”?请说明理由;(2)、若 , 为 , 的“2重覆盖函数”,求实数的取值范围;(3)、函数表示不超过的最大整数,如 . 若为的“2024重覆盖函数”,求正实数的取值范围.
-
15、如图,在正方体中,为的中点.
 (1)、求证:平面;(2)、连接交于点 , 求三棱锥的体积;(3)、已知点为中点,点为平面内的一个动点,若平面 , 求长度的最小值.
(1)、求证:平面;(2)、连接交于点 , 求三棱锥的体积;(3)、已知点为中点,点为平面内的一个动点,若平面 , 求长度的最小值. -
16、如图,在菱形中,分别是边的中点,与交于点 , 设 .
 (1)、用表示;(2)、求的余弦值.
(1)、用表示;(2)、求的余弦值. -
17、已知函数的最小正周期为 .(1)、求的值;(2)、求在上的值域.
-
18、球面被平面所截得的一部分叫做球冠,截得的圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠的高球体被平面截下的一部分几何体叫做球缺,截面叫做球缺的底面,垂直于截面的直径被截下的线段长叫做球缺的高,球缺是旋转体,可以看做是球冠和其底所在的圆面所围成的几何体.如图1,一个球面的半径为 , 球冠的高是 , 球冠的表面积公式是 , 与之对应的球缺的体积公式是 . 如图2,已知是以为直径的圆上的两点, , 则扇形绕直线旋转一周形成的几何体的表面积为 , 体积为 .

-
19、勒洛三角形是一种典型的定宽曲线,以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形就是勒洛三角形.在如图所示的勒洛三角形中,已知为弧(含端点)上的一点,则的范围为 .

-
20、已知函数 , 则 .