相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、某学校对高三(1)班50名学生第一次模拟考试的数学成绩和化学成绩统计得到数据如下:数学成绩的方差为 , 化学成绩的方差为 , 其中且1分别表示这50名学生的数学成绩和化学成绩,关于的线性回归方程为.(1)、求与的样本相关系数;(2)、从概率统计规律来看,本次考试高三(1)班学生数学成绩服从正态分布 , 用样本平均数作为的估计值,用样本方差作为的估计值.试估计该校共800名高三学生中,数学成绩位于区间的人数.
附:①回归方程中:
②样本相关系数
③若 , 则
④
-
2、欧拉公式是由瑞士著名数学家欧拉创立,将其中的取就得到了欧拉恒等式,数学家评价它是“上帝创造的公式”.已知复数满足 , 则的最大值为( )A、 B、1 C、 D、
-
3、如图所示,六氟化硫分子结构是六个氟原子处于顶点位置,而硫原子处于中心位置的正八面体,也可将其六个顶点看作正方体各个面的中心点.若正八面体的表面积为 , 则正八面体外接球的体积为( )
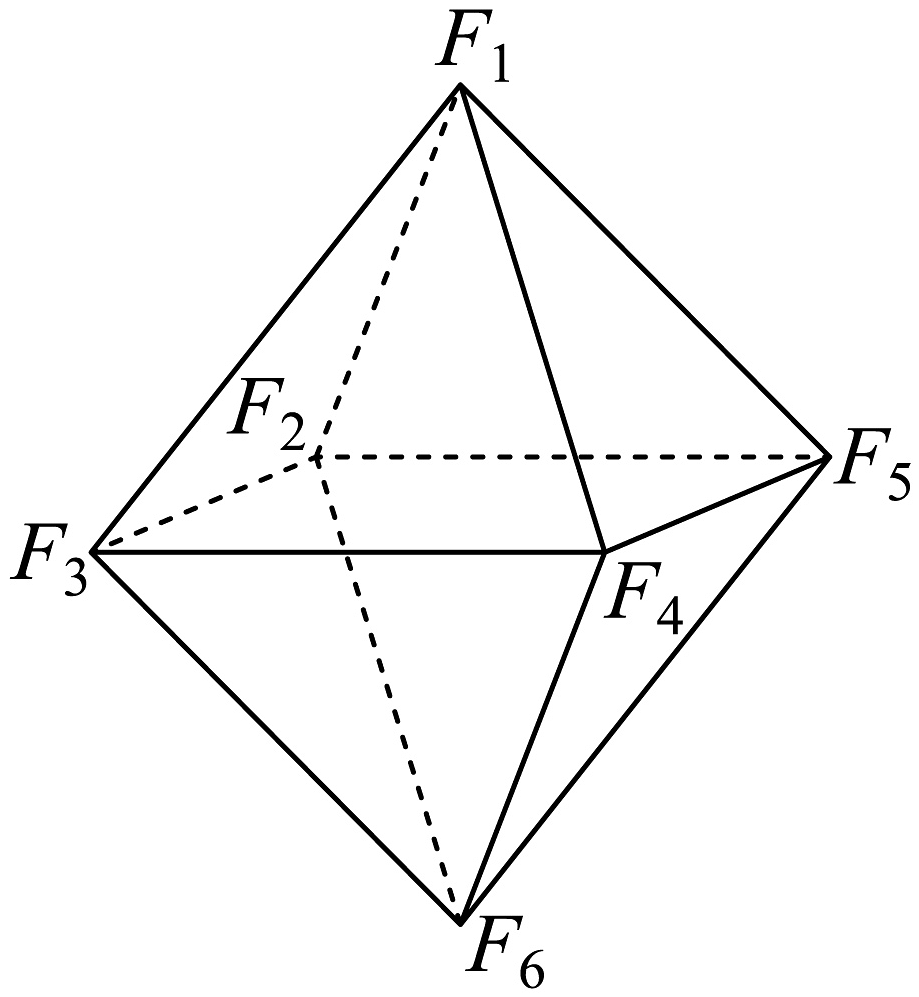 A、 B、 C、 D、
A、 B、 C、 D、 -
4、若命题:“ , , 使得”为假命题,则 , 的大小关系为( )A、 B、 C、 D、
-
5、已知函数的图象过点 , 且.(1)、求 , 的值;(2)、求函数的极值.
-
6、随着AI技术的不断发展,人工智能科技在越来越多的领域发挥着重要的作用.某校在寒假里给学生推荐了一套智能辅导系统,学生可自愿选择是否使用该系统完成假期的作业.开学时进行了入学测试,随机抽取了100名学生统计得到如下列联表:
使用智能辅导系统
未使用智能辅导系统
合计
入学测试成绩优秀
20
20
40
入学测试成绩不优秀
40
20
60
合计
60
40
100
(1)、判断是否有95%的把握认为入学测试成绩优秀与使用智能辅导系统相关;(2)、若把这100名学生按照入学测试成绩是否优秀进行分层随机抽样,从中抽取5人,再从这5人中随机抽取2人,记抽取的2人中入学测试成绩优秀的人数为 , 求的分布列及数学期望 .附: , 其中 .
0.10
0.05
0.025
0.010
2.706
3.841
5.024
6.635
-
7、若 , , 则是的条件.
-
8、若 , 给出下列不等式正确的是( )A、 B、 C、 D、
-
9、函数的图象大致是( )A、
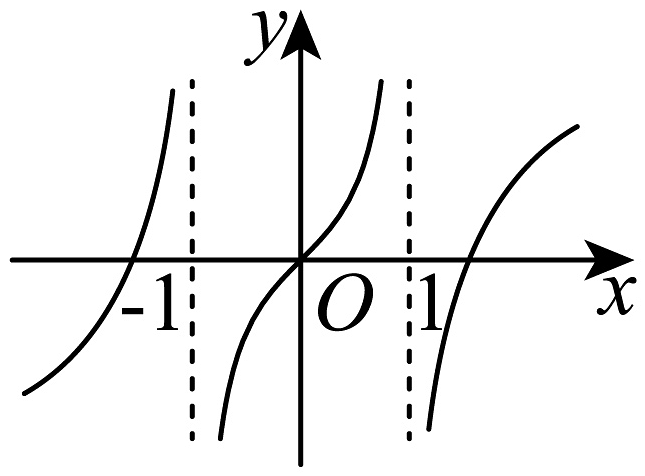 B、
B、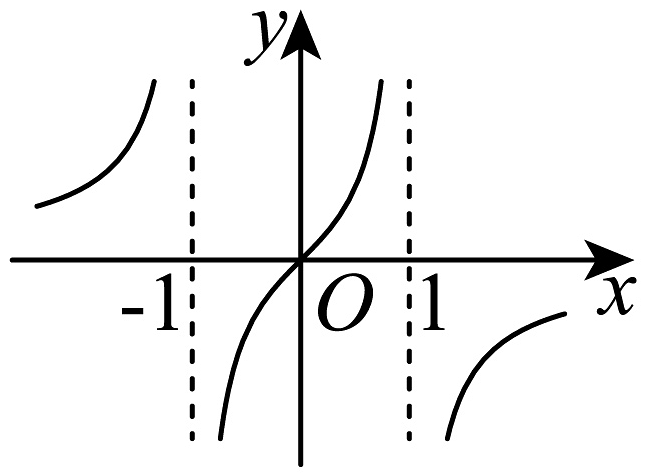 C、
C、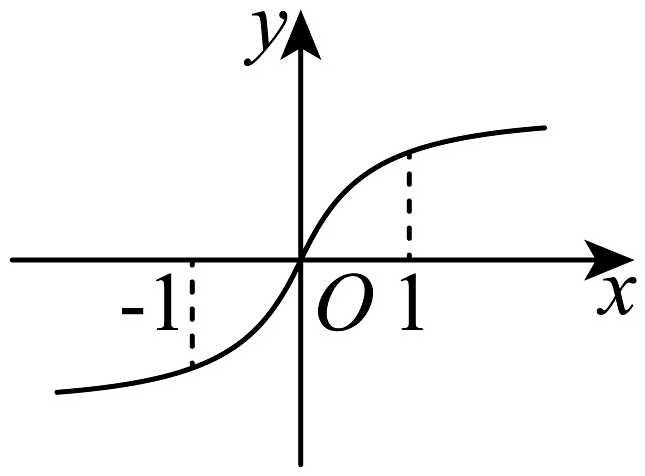 D、
D、
-
10、下列命题为真命题的是( )A、若 , 则 B、若 , , 则 C、若 , 则 D、若 , 则
-
11、“一元二次方程有实数根”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
12、函数的定义域为( )A、 B、 C、 D、
-
13、已知抛物线的焦点为 , 准线交轴于点 , 直线经过且与交于两点,其中点A在第一象限,线段的中点在轴上的射影为点.若 , 则( )A、的斜率为 B、是锐角三角形 C、四边形的面积是 D、
-
14、现定义:若对于集合满足:对任意 , 都有 , 则称是可分比集合.(1)、证明:是可分比集合;(2)、设集合均为可分比集合,且 , 求正整数的最大值;(3)、探究是否存在正整数 , 对于任意正整数 , 均存在可分比集合 , 使得 . 若存在,求的最小值;若不存在,说明理由.
-
15、已知函数 .(1)、当时,求的最小值;(2)、当时,求零点的个数;(3)、当时, , 求的取值范围.
-
16、如图,五面体中,底面四边形为边长为的正方形, .
 (1)、证明:;(2)、已知为线段的中点,点在平面上的投影恰为线段的中点,直线与平面所成角的正切值为 , 求直线与平面所成角的正弦值.
(1)、证明:;(2)、已知为线段的中点,点在平面上的投影恰为线段的中点,直线与平面所成角的正切值为 , 求直线与平面所成角的正弦值. -
17、已知中,角的对边分别为 , 且 .(1)、求;(2)、若 , 求面积的最大值.
-
18、仙人掌别名老鸦舌,神仙掌,这一独特的仙人掌科草本植物,以其顽强的生命力和独特的形态在自然界中独树一帜,以其形似并拢手指的手掌,且带有刺的特征而得名.仙人掌不仅具有极高的观赏价值,还具有一定的药用价值,被誉为“夜间氧吧”,其根茎深入土壤或者干燥的黄土中使其能够吸收足够多的水分进行储藏来提高生存能力,我国某农业大学植物研究所相关人员为了解仙人掌的植株高度y(单位:cm),与其根茎长度x(单位:cm)之间是否存在线性相关的关系,通过采样和数据记录得到如下数据:
样本编号
1
2
3
4
根茎长度
10
12
14
16
植株高度
62
86
112
132
参考数据: .
(1)、由上表数据计算相关系数 , 并说明是否可用线性回归模型拟合与的关系(若 , 则可用线性回归模型拟合,计算结果精确到0.001);(2)、求关于的线性回归方程.附:对于一组数据 , 其回归直线的斜率和截距的最小二乘法估计公式,相关系数的公式分别为 .
-
19、已知数列中, , 则 .
-
20、已知函数在区间上有且仅有1个零点,则最小正周期的最小值为 .