版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、一年一度的“双11”促销活动落下帷幕，各大电商平台发布的数据显示，在消费品以旧换新、家电政府补贴等促消费政策和活动的带动下，消费市场潜能加速释放，带动相关商品销售保持增长. 经过调研，得到2019年到2024年“双11”活动当天某电商平台线上日销售额 $y$ （单位：百亿元）与年份（第 $x$ 年）的6组数据（时间变量 $x$ 的取值依次为 $1, 2, \cdot \cdot \cdot, 6$ ），对数据进行处理，得到如下散点图（图1）及一些统计量的值. 其中 $t_{i} = \ln x_{i}, \bar{t} = \frac{1}{6} \sum_{i = 1}^{6} t_{i}$ .
$\bar{y}$
$\bar{x}$
$\sum_{i = 1}^{6} x_{i}^{2}$
$\sum_{i = 1}^{6} x_{i} y_{i}$
$\bar{t}$
$\sum_{i = 1}^{6} t_{i}^{2}$
$\sum_{i = 1}^{n} t_{i} y_{i}$
48.7
3.5
91
1204
1.1
9.4
388.1
分别用两种模型：① $y = b x + a$ ；② $y = b \ln x + a$ 进行拟合，得到相应的回归方程，并进行残差分析，得到如图所示的残差图（图2）（残差值 $=$ 真实值 $-$ 预测值）.

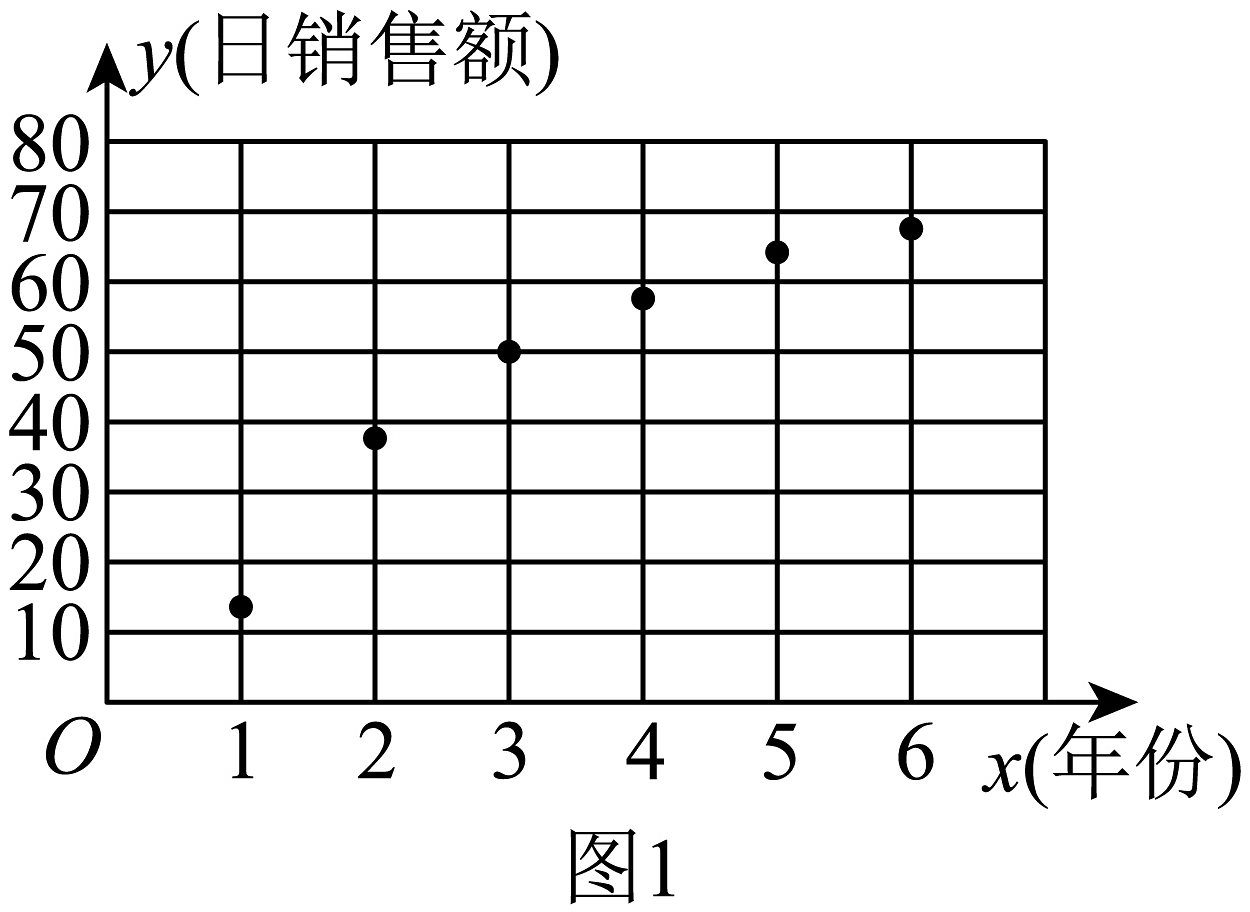
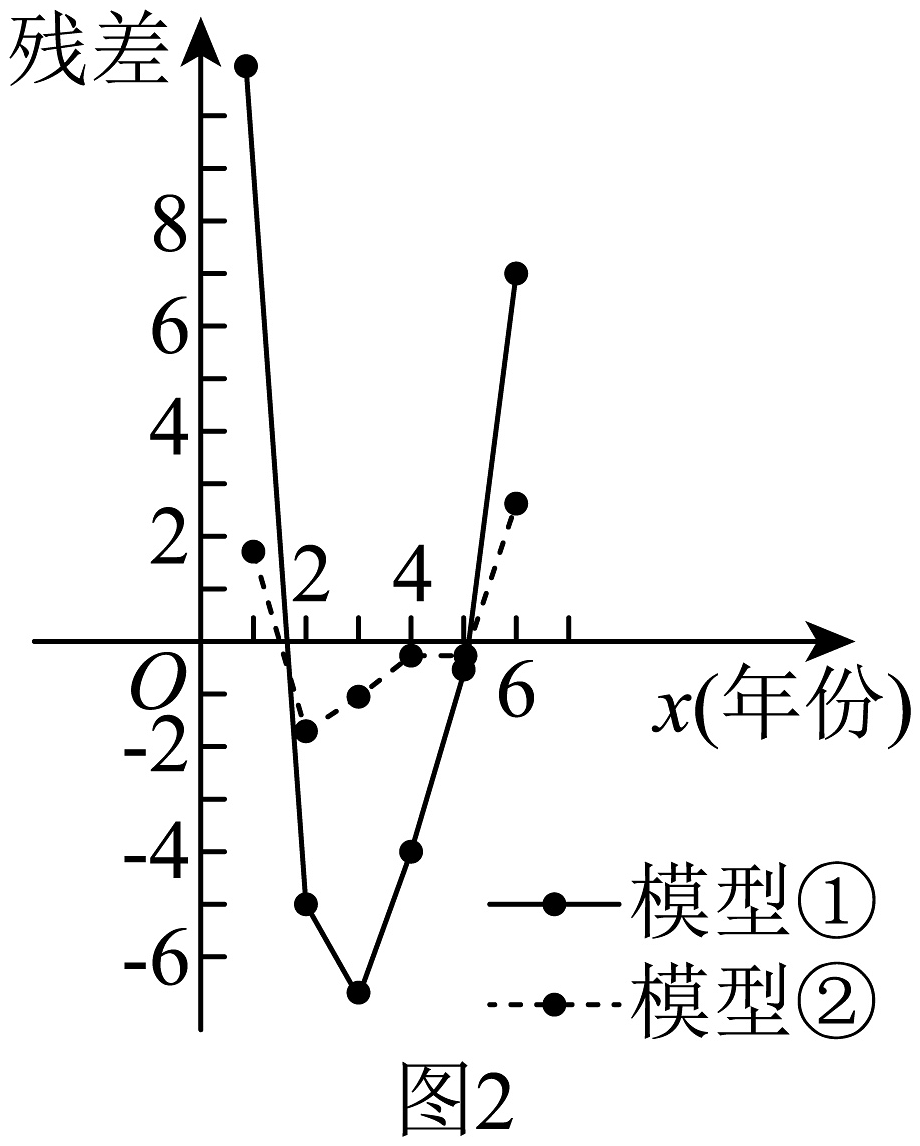(1)、根据题中信息，通过残差图比较模型①，②的拟合效果，应选择哪一个模型进行拟合？请说明理由；

(2)、根据（1）中所选模型，
（i）求出 $y$ 关于 $x$ 的经验回归方程（系数精确到0.1）；
（ⅱ）若该电商平台每年活动当天线上日销售额 $y$ 与当日营销成本 $u$ 及年份 $x$ 存在线性关系： $y = 3 u + 2.6 x$ ，则在第几年活动当日营销成本的预测值最大?
参考公式： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \cdot \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}, \hat{a} = \bar{y} - \hat{b} \bar{x}$ ；参考数据： $\ln 7 \approx 1.95$ .

查看解析
2、已知 $cos (x - \frac{π}{10}) = - \frac{4}{5}$ ，则 $sin (2 x + \frac{3 π}{10}) =$ .

查看解析
3、微分中值定理是微积分学中的重要定理，它是研究区间上函数值变化规律的有效工具，其中拉格朗日中值定理是核心，它的内容如下：
如果函数 $f (x)$ 在闭区间 $[a, b]$ 上连续，在开区间 $(a, b)$ 可导，导数为 $f^{'} (x)$ ，那么在开区间 $(a, b)$ 内至少存在一点 $c$ ，使得 $f^{'} (c) = \frac{f (b) - f (a)}{b - a}$ ，其中 $c$ 叫做 $f (x)$ 在 $[a, b]$ 上的“拉格朗日中值点”.已知函数 $f (x) = \frac{(a + 1) x^{2}}{4} \ln x + b^{2} (x - 4) e^{a x} - \frac{b^{2}}{6} x^{3} + (\frac{9 b + 15}{8}) x^{2}$ .

(1)、若 $a = - 1, b = 0$ ，求函数 $f (x)$ 在 $[1, 7]$ 上的“拉格朗日中值点” $x_{0}$ ；

(2)、若 $a = - 1, b = 1$ ，求证：函数 $f (x)$ 在区间 $(0, + \infty)$ 图象上任意两点 $A$ ， $B$ 连线的斜率不大于 $18 - e^{- 6}$ ；

(3)、若 $a = 1, b = - 1, \forall x_{1}, x_{2}, x_{3} \in (\frac{1}{4}, 1)$ ，且 $x_{1} < x_{2} < x_{3}$ ，求证： $\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} > \frac{f (x_{3}) - f (x_{2})}{x_{3} - x_{2}}$ .

查看解析
4、非零向量 $\overset{⃑}{m}, \overset{⃑}{n}$ 的夹角为 $\frac{π}{3}$ ，且满足 $| \vec{n} |= λ| \vec{m} |(λ⟩ 0)$ ，向量组 $x_{1}, x_{2}, x_{3}$ 由一个 $\overset{⃑}{m}$ 和两个 $\overset{⃑}{n}$ 排列而成，向量组 $y_{1}, y_{2}, y_{3}$ 由两个 $\overset{⃑}{m}$ 和一个 $\overset{⃑}{n}$ 排列而成，若 $x_{1} \cdot y_{1} + x_{2} \cdot y_{2} + x_{3} \cdot y_{3}$ 所有可能值中的最小值为 $4 {\overset{⃑}{m}}^{2}$ ，则 $λ =$ ．

查看解析
5、已知幂函数 $f (x) = x^{- k^{2} + k + 2}, (k \in Z)$ 满足 $f (2) < f (3)$ ，若函数 $g (x) = 1 - q f (x) + (2 q - 1) x$ ，在区间 $[- 1, 2]$ 上是减函数，则非负实数 $q$ 的取值范围是．

查看解析
6、下列命题错误的是：（）

A、两平行直线 $5 x + 12 y + 3 = 0$ 与 $10 x + 24 y + 5 = 0$ 之间的距离是 $\frac{1}{26}$ B、若点 $A (- 2, - 3)$ ， $B (- 3, - 2)$ ，直线l过点 $P (1, 1)$ 且与线段 $A B$ 相交，则l的斜率k的取值范围是 $k \leq - \frac{4}{3}$ 或 $k \geq - \frac{3}{4}$ C、若点 $M (x_{0}, y_{0})$ 在圆 $x^{2} + y^{2} = R^{2}$ 外，则直线 $x_{0} x + y_{0} y = R^{2}$ 与圆相离 D、若 $3 a^{2} + 3 b^{2} - 4 c^{2} = 0$ ，则直线 $a x + b y + c = 0$ 被圆 $x^{2} + y^{2} = 1$ 所截得的弦长为1

查看解析
7、已知函数 $f (x) = x + e^{x}$ ， $g (x) = x e^{x}$ ，若 $f (m) = a$ ， $g (n) = e^{a}$ ，则 $a n e^{e^{m}}$ 的最小值为（）

A、 $\frac{1}{e}$ B、e C、 $- e$ D、 $- \frac{1}{e}$

查看解析
8、在等比数列 ${a_{n}}$ 中 $a_{1} = 3$ ，其前n项和为 $S_{n} .$ 若数列 ${a_{n} + 3}$ 也是等比数列，则 $S_{n}$ 等于 $($ 　　 $)$

A、 $\frac{3^{n + 1} - 3}{2}$ B、3n C、 $2 n + 1$ D、 $3 \times 2^{n} - 3$

查看解析
9、已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的上顶点为A，左、右两焦点分别为 $F_{1}$ ， $F_{2}$ ，若 $△ A F_{1} F_{2}$ 为等边三角形，则椭圆C的离心率为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{3}$ D、 $\frac{\sqrt{3}}{3}$

查看解析
10、若函数 $f (x)$ 在定义域区间 $[a, b]$ 上连续，对任意 $x_{1}, x_{2} \in [a, b]$ 恒有 $f (\frac{x_{1} + x_{2}}{2}) \geq$ $\frac{f (x_{1}) + f (x_{2})}{2}$ ，则称函数 $f (x)$ 是区间 $[a, b]$ 上的上凸函数，若恒有 $f (\frac{x_{1} + x_{2}}{2}) \leq \frac{f (x_{1}) + f (x_{2})}{2}$ ，则称函数 $f (x)$ 是区间 $[a, b]$ 上的下凸函数，当且仅当 $x_{1} = x_{2}$ 时等号成立，这个性质称为函数的凹凸性．上述不等式可以推广到取函数定义域中的任意n个点，即若 $f (x)$ 是上凸函数，则对任意 $x_{1}, x_{2}, \dots, x_{n} \in [a, b]$ 恒有 $f (\frac{x_{1} + x_{2} + \cdot \cdot \cdot + x_{n}}{n}) \geq \frac{f (x_{1}) + f (x_{2}) + \cdot \cdot \cdot + f (x_{n})}{n}$ ，若 $f (x)$ 是下凸函数，则对任意 $x_{1}, x_{2}, \dots, x_{n} \in [a, b]$ 恒有 $f (\frac{x_{1} + x_{2} + \cdot \cdot \cdot + x_{n}}{n}) \leq \frac{f (x_{1}) + f (x_{2}) + \cdot \cdot \cdot + f (x_{n})}{n}$ ，当且仅当 $x_{1} = x_{2} = \cdot \cdot \cdot = x_{n}$ 时等号成立．应用以上知识解决下列问题：

(1)、判断函数 $f (x) = a x^{2} + b x + c$ （ $a \neq 0$ ， $x \in R$ ）， $g (x) = \sin x$ ， $x \in (0, π)$ 在定义域上是上凸函数还是下凸函数；（只写出结论，不需证明）

(2)、利用（1）中的结论，在 $△ A B C$ 中，求 $\sin A + \sin B + \sin (A + B)$ 的最大值；

(3)、证明函数 $h (x) = a \ln \frac{1}{x} - x^{2} - \frac{2}{x} (a \leq 0)$ 是上凸函数．

查看解析
11、如图，一艘货轮从码头O出发沿北偏东30°的OD方向以20海里/小时的速度驶往目的地，出发后发现燃料不足，立即联系位于O正东方向120海里的A处的加油船在中途加油补充燃料，假设加油船与货轮同时出发，但加油船要先到小岛B处补给物资再赶往货轮处，已知小岛B在码头O北偏东60°方向，也在A北偏西30°方向上，加油船在B处补给物资需要1个小时，且加油船航行速度始终为60海里/小时．

(1)、求加油船到达小岛B所需的时间；

(2)、两艘船最少经过多少小时能相遇？

查看解析
12、已知函数 $f (x) = \frac{1}{2^{x} + m}$ ．

(1)、是否存在 $m \in R$ ，使得 $f (x) + f (2 - x)$ 为定值，若存在，求出m的值；若不存在，说明理由；

(2)、若 $m = 1$ ，方程 $|f (x) - \frac{1}{2}| = k f (x) (k \in R)$ 有两个根 $x_{1}$ ， $x_{2}$ ，且 $x_{1} < 0$ ， $x_{2} > 0$ ，求 $x_{1} + x_{2}$ 的取值范围．

查看解析
13、已知函数 $f (x) = \sin^{2} x - \cos^{2} x - \sqrt{3} \sin (2 x - \frac{π}{3})$ ．

(1)、求 $f (x)$ 的最小正周期及单调递增区间；

(2)、若 $f (x) = \frac{\sqrt{3}}{2}$ ，求 $\tan x$ 的值．

查看解析
14、在平面直角坐标系中，已知向量 $\vec{A B} = (1, 2)$ ， $\vec{B C} = (x - 1, y)$ ， $\vec{C D} = (2 x, - 2 y)$ ，且 $\vec{B C}$ ， $\vec{C D}$ 为非零向量．

(1)、若B是AD的中点，求 $\vec{B C}$ 的坐标；

(2)、若 $\vec{A B} / / \vec{C D}$ ， $\vec{A C} ⊥ \vec{B D}$ ，求四边形ABCD的面积．

查看解析
15、已知 $△ A B C$ 中 $A B = 2$ ，点 $D$ 满足 $\vec{B D} = 2 \vec{D C}$ ，且 $\vec{A D} = \frac{{\vec{A B}}^{2} \cdot \vec{A C} + {\vec{A C}}^{2} \cdot \vec{A B}}{{\vec{A B}}^{2} + {\vec{A C}}^{2}}$ ，点 $O$ 是 $△ A B C$ 的外心，则 $\vec{A O} \cdot \vec{B C} =$ ．

查看解析
16、已知复数z满足 $| z | \leq 2$ ，且 $\frac{| z - 1 |}{| z - i |} = 1$ ，则复数z表示的轨迹长为．

查看解析
17、已知 $△ A B C$ 中，角A，B，C的对边分别为a，b，c， $\sin^{2} B + \sin^{2} A = \sin^{2} C + \frac{3}{2} \sin B \sin A$ ，则 $\sin C =$ ．

查看解析
18、定义在 $R$ 上的偶函数 $f (x)$ 满足 $f (x + 1) = f (x - 3)$ ， $x \in [- 2, 0]$ 时 $f (x) = x^{2}$ ，则（）

A、 $f (x)$ 是周期为4的函数 B、 $f (x)$ 相邻两条对称轴间的距离为4 C、 $x \in [4, 6]$ 时， $f (x) = 3$ 的解是 $4 + \sqrt{3}$ D、若 $y = f (x) - 1, x \in [m, n]$ （ $n > m$ ）有2024个零点，则 $n - m$ 的最小值是4047

查看解析
19、已知非零向量 $\vec{a}$ ， $\vec{b}$ 满足 $\sqrt{3} |\vec{a}| = \sqrt{3} |\vec{b}| = |\vec{a} - \vec{b}|$ ，则（）

A、 $\vec{a}$ ， $\vec{b}$ 的夹角为 $\frac{π}{3}$ B、 $|\vec{a} + \vec{b}| = |\vec{a}|$ C、若 $\vec{O A} = \vec{a}$ ， $\vec{O B} = \vec{b}$ ，则 $△ O A B$ 的外接圆半径长为 $|\vec{a}|$ D、若 $|\vec{a}| = 1$ ，向量 $\vec{c}$ 满足 $(\vec{c} - \vec{a}) \cdot (\vec{c} - \vec{b}) = 0$ ，则 $|\vec{c}|$ 的最大值是 $\frac{\sqrt{3}}{2} + \frac{1}{2}$

查看解析
20、若函数 $f (x)$ 的图象关于点 $(1, 0)$ 对称， $f (x)$ 在定义域 $R$ 上单调递增，则不等式 $f (\sin x + 3) + f (\sqrt{3} \cos x) > 0$ 的解是（）

A、 $(\frac{5 π}{6}, \frac{3 π}{2})$ B、 $(2 k π - \frac{π}{3}, 2 k π + \frac{5 π}{6})$ ， $k \in Z$ C、 $(2 k π - \frac{π}{2}, 2 k π + \frac{5 π}{6})$ ， $k \in Z$ D、 $(k π - \frac{π}{3}, k π + \frac{2 π}{3})$ ， $k \in Z$

查看解析

上一页 610 611 612 613 614 下一页跳转

$\bar{y}$	$\bar{x}$	$\sum_{i = 1}^{6} x_{i}^{2}$	$\sum_{i = 1}^{6} x_{i} y_{i}$	$\bar{t}$	$\sum_{i = 1}^{6} t_{i}^{2}$	$\sum_{i = 1}^{n} t_{i} y_{i}$
48.7	3.5	91	1204	1.1	9.4	388.1