相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、下列关系中,表述正确的是( )A、 B、
 A
C、
D、
A
C、
D、
-
2、如图,在四棱锥中,平面平面 , , , , .
 (1)、求证:平面平面;(2)、若 , , 点是线段上一点,且二面角的余弦值为 , 求的值.
(1)、求证:平面平面;(2)、若 , , 点是线段上一点,且二面角的余弦值为 , 求的值. -
3、如图,在八面体中,四边形是边长为2的正方形,平面平面 , 二面角与二面角的大小都是 , , .
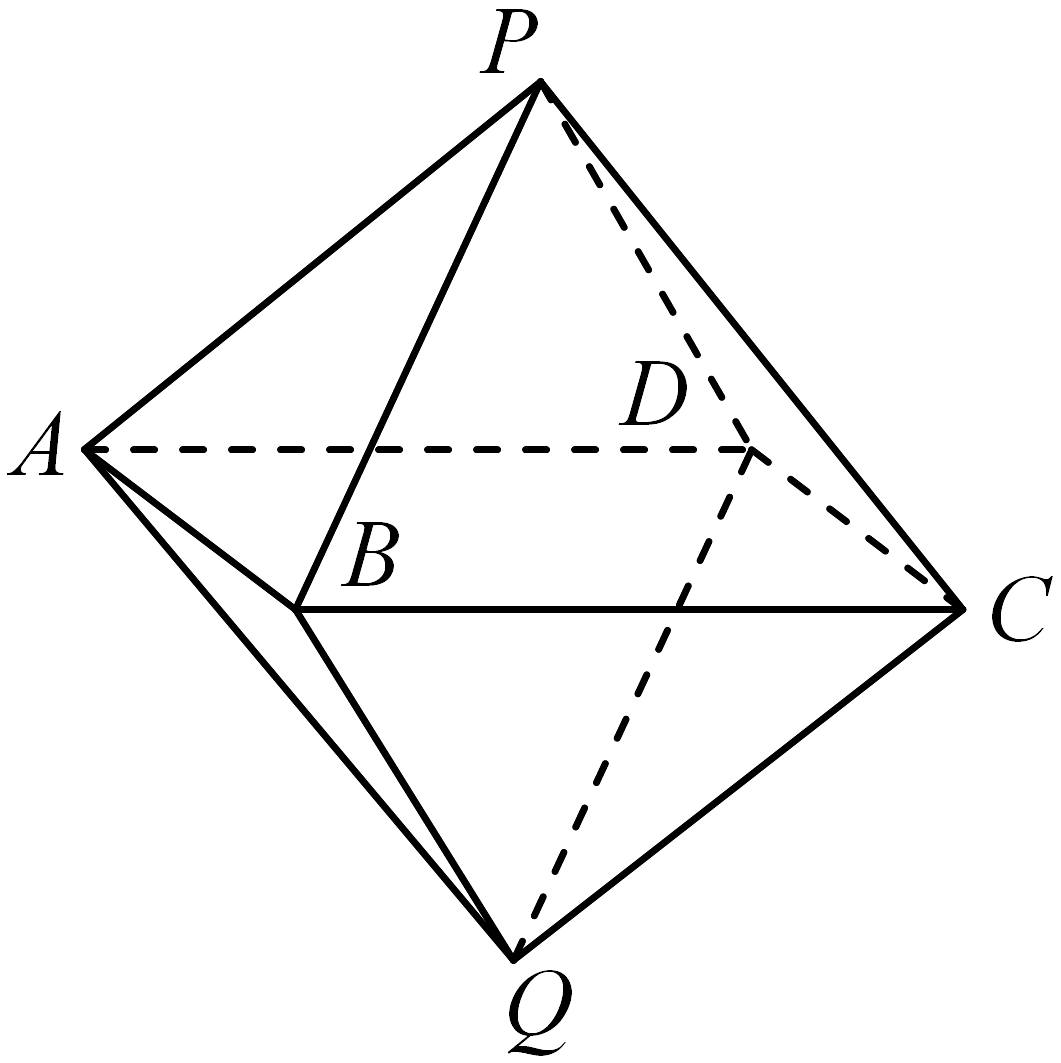 (1)、证明:平面平面;(2)、设为的重心,是否在棱上存在点 , 使得与平面所成角的正弦值为 , 若存在,求到平面的距离,若不存在,说明理由.
(1)、证明:平面平面;(2)、设为的重心,是否在棱上存在点 , 使得与平面所成角的正弦值为 , 若存在,求到平面的距离,若不存在,说明理由. -
4、已知函数满足 , 且 , 当时, . 函数 .(1)、求实数的值;(2)、当时,求的解析式;(3)、设 , 是否存在实数 , 使不等式在时恒成立?若存在,求实数的取值范围;若不存在,请说明理由.
-
5、某市环保部门对市中心每天的环境污染情况进行调查研究后,发现一天中环境综合污染指数与时刻(时)的关系为 , , 其中是与气象有关的参数,且 , 若用每天的环境综合污染指数的最大值作为当天的综合污染指数,并记作 .(1)、当时,求环境综合污染指数的值域;(2)、求的解析式;(3)、规定当时为综合污染指数超标,求当在什么范围内时,该市市中心的综合污染指数超标.
-
6、已知的三个内角所对的边分别为 , 满足 .(1)、求;(2)、若为锐角三角形,且 , 求的周长的取值范围.
-
7、人脸识别就是利用计算机分析人脸视频或者图像,并从中提取出有效的识别信息,最终判别人脸对象的身份.在人脸识别中为了检测样本之间的相似度主要应用距离的测试,常用的测量距离的方式有曼哈顿距离和余弦距离.已知二维空间两个点、 , 则其曼哈顿距离为 , 余弦相似度为 , 余弦距离为 . 已知 , 、、、 , 若 , , 则 .
-
8、在中,是的中点, , , , 则 .
-
9、已知向量 , , 则向量在向量上的投影向量的坐标为 .
-
10、已知函数的定义域为 , , 为奇函数,且 , 则( )A、 B、 C、函数是偶函数 D、(参考公式:)
-
11、已知圆台的上、下底面半径分别为1和3,母线长为 , 则( )A、圆台的母线与底面所成的角为 B、圆台的侧面积为 C、圆台的体积为 D、若圆台的两个底面的圆周在同一个球的球面上,则该球的表面积为
-
12、下列说法正确的是( )A、若 , , 则 B、若 , 则 C、若 , , , 则的最小值为4 D、若 , , , 则的最小值为4
-
13、某工业园区有、、共3个厂区,其中 , , , 现计划在工业园区内选择处建一仓库,若 , 则的最小值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、函数的图象在区间上恰有一条对称轴和一个对称中心,则( )A、 B、当时,在区间上不单调 C、在区间上无最大值 D、在区间上的最小值为
-
15、“”是“函数在区间上单调递增”的( )A、充分不必要条件 B、充要条件 C、必要不充分条件 D、既不充分也不必要条件
-
16、集合满足 , , , 则集合中的元素个数为( )A、3 B、4 C、5 D、6
-
17、若数列满足 , 则称数列为项数列,由所有项数列组成集合.(1)、若是12项0数列,当且仅当时, , 求数列的所有项的和;(2)、从集合中任意取出两个数列 , 记.
①求随机变量的分布列,并证明:;
②若用某软件产生项数列,记事件“第一次产生数字1”,“第二次产生数字1”,且.若 , 比较与的大小.
-
18、一个袋子中有10个大小相同的球,其中红球7个,黑球3个.每次从袋中随机摸出1个球,摸出的球不再放回.设第1,2,3次都摸到红球的概率为;在第1,2次都摸到红球的条件下,第3次摸到红球的概率为.求.
-
19、如图,一个底面半径为2dm,母线长为的圆锥形封闭透明容器内部装有一种液体,当圆锥底面向下平放在水平桌面上时,液面的高度恰好为圆锥的高的 , 则当圆锥的顶点在桌面上,且底面平行于水平桌面时,液面的高度为( )
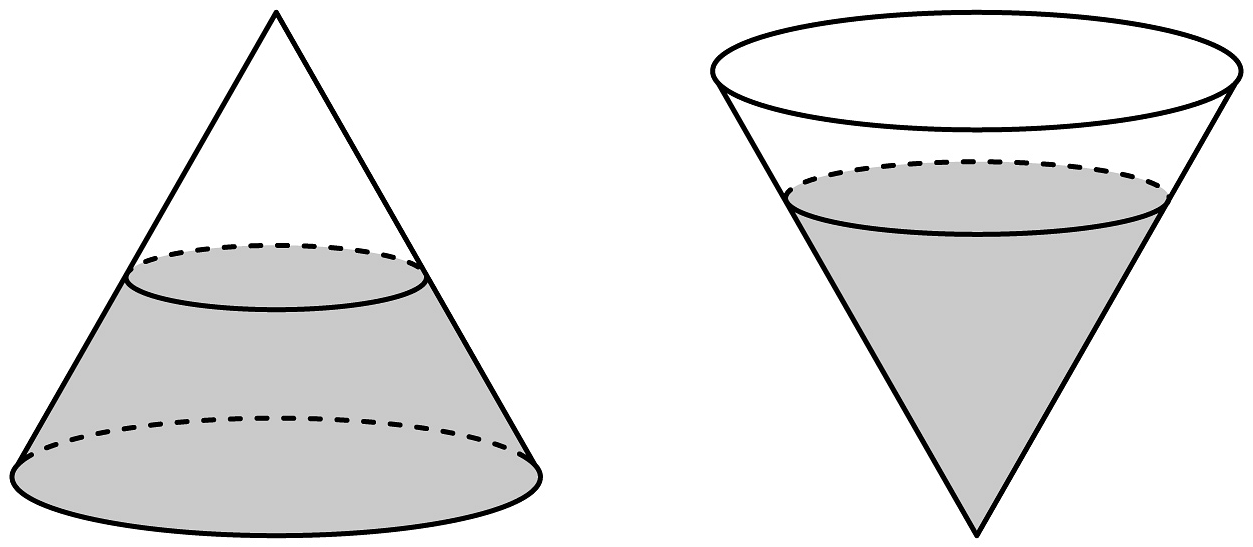 A、 B、2dm C、3dm D、
A、 B、2dm C、3dm D、 -
20、已知 , , 则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则