相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、某商场举行有奖促销活动,购满100元商品得1张奖券,多购多得.1000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为 , 则1张奖券的中奖概率为.
-
2、图(1)为棱长为1的正方体,若正方体内有两个球相外切且又分别与正方体的三个面相切,则两球半径之和为.
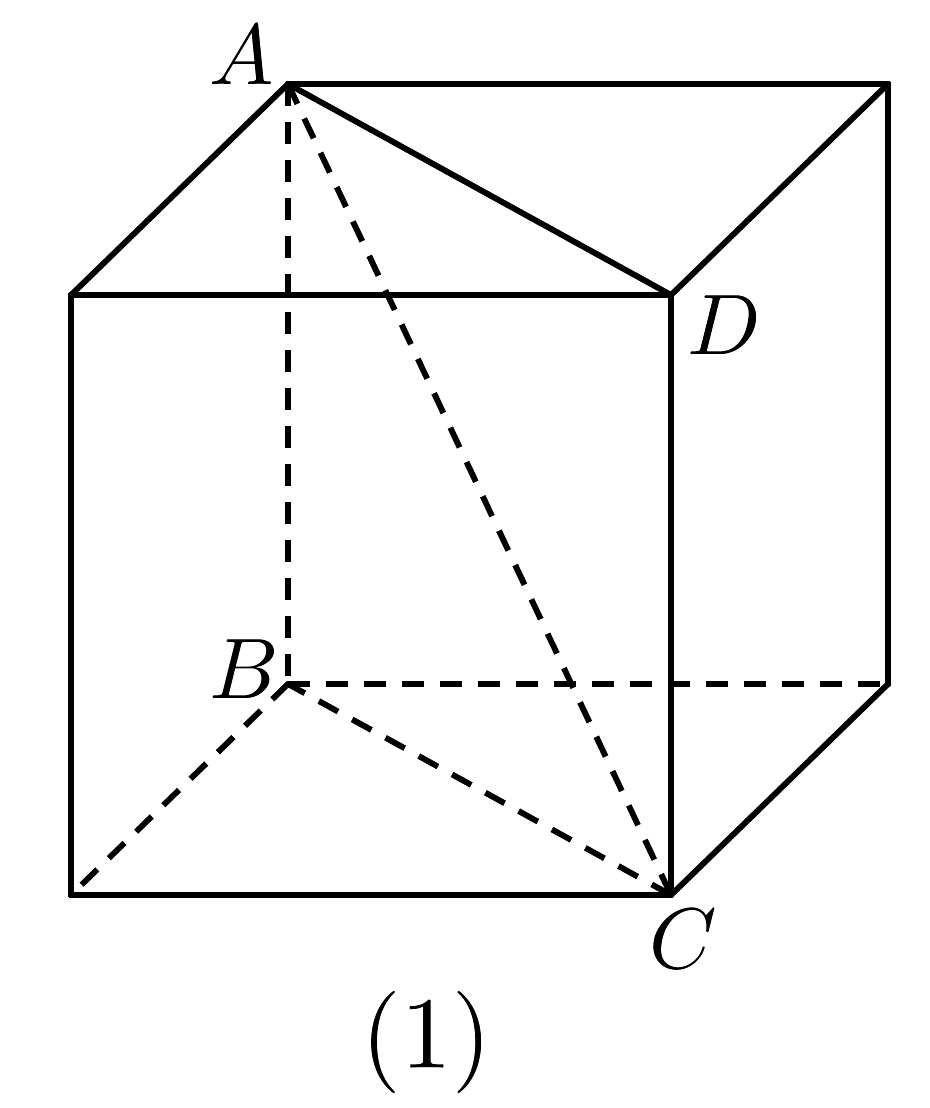
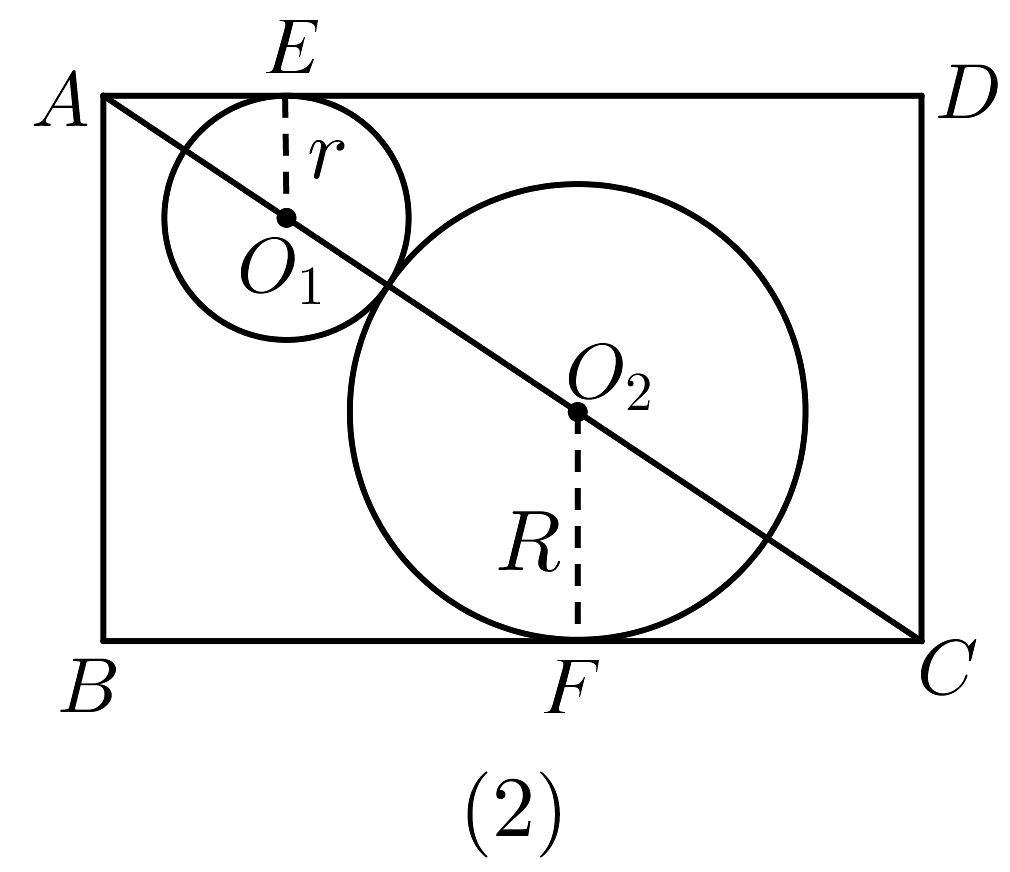
-
3、已知点 , (),试求当点在第三象限时,的取值范围 .
-
4、已知正四棱柱的底面边为1,侧棱长为 , 是的中点,
 则( )A、任意 , B、存在 , 直线与直线相交 C、平面与底面交线长为定值 D、当时,三棱锥外接球表面积为
则( )A、任意 , B、存在 , 直线与直线相交 C、平面与底面交线长为定值 D、当时,三棱锥外接球表面积为 -
5、下列运算结果正确的是( ).A、已知 , 若 , 则 B、已知点 , 则向量在方向上的投影数量为 C、已知向量 , 若 , 则 D、向量不共线,点在线段上,且 , 则
-
6、已知是虚数单位,则下列说法正确的有( ).A、 B、“”是“复数是纯虚数”的必要不充分条件 C、若复数 , 且 , 则 D、若复数满足 , 则复数的虚部为-2
-
7、将函数图象上各点横坐标缩短到原来的 , 再向右平移个单位得到曲线 . 若曲线的图象关于原点对称,则函数的一条对称轴可以为( )A、 B、 C、 D、
-
8、已知集合 , , 若 , 则的值为( )A、1 B、2 C、1或2 D、1或
-
9、池州九华山是著名的旅游胜地.天气预报8月1日后连续四天,每天下雨的概率为0.6.现用随机模拟的方法估计四天中恰有三天下雨的概率:在0~9十个整数值中,假定0,1,2,3,4,5表示当天下雨,6,7,8,9表示当天不下雨.在随机数表中从某位置按从左到右的顺序读取如下40组四位随机数:
9533 9522 0018 7472 0018 3879 5869 3281 7890 2692
8280 8425 3990 8460 7980 2436 5987 3882 0753 8935
9635 2379 1805 9890 0735 4640 6298 8054 9720 5695
1574 8008 3216 6470 5080 6772 1642 7920 3189 0343
据此估计四天中恰有三天下雨的概率为( )
A、 B、 C、 D、 -
10、下列统计量中可用于度量样本离散程度的有( )A、的标准差 B、的中位数 C、的众数 D、的平均数
-
11、已知两条不同的直线m、和两个不同的平面 , 下列命题是真命题的为( )A、若m , ⊥m,则⊥α B、若β,⊥ , , 则⊥m C、若m , ⊥ , 则m⊥ D、若m , , 则m
-
12、设z=-3+2i,则在复平面内对应的点位于A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
13、水污染现状与工业废水排放密切相关.某工厂深入贯彻科学发展观,努力提高污水收集处理水平,其污水处理程序如下:原始污水必先经过系统处理,处理后的污水(级水)达到环保标准(简称达标)的概率为 . 经化验检测,若确认达标便可直接排放;若不达标则必须进入系统处理后直接排放.某厂现有4个标准水量的级水池,分别取样、检测.多个污水样本检测时,既可以逐个化验,又可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水可直接排放.现有以下四种方案:
方案一:逐个化验;
方案二:平均分成两组化验;
方案三:三个样本混在一起化验,剩下的一个单独化验;
方案四:四个样本混在一起化验.
若化验次数的期望值越小,则方案越“优”.
(1)若 , 现有4个级水样本需要化验,请问:方案一、二、四中哪个最“优”?
(2)若“方案三”比“方案四”更“优”,求的取值范围.
-
14、记是各项均不为零的数列的前n项和,已知 .(1)、求数列的通项公式;(2)、若 , 求数列的前n项和 .
-
15、在年春节期间,为了进一步发挥电子商务在活跃消费市场方面的积极作用,保障人民群众度过一个平安健康快乐祥和的新春佳节,甲公司和乙公司在某购物平台上同时开启了打折促销、直播带年货活动,甲公司和乙公司所售商品类似,存在竞争关系.(1)、现对某时间段名观看直播后选择这两个公司直播间购物的情况进行调查,得到如下数据:
选择甲公司直播间购物
选择乙公司直播间购物
合计
用户年龄段岁
用户年龄段岁
合计
请将表格补充完整,并判断是否有的把握认为选择哪家直播间购物与用户的年龄有关?
(2)、若小李连续两天每天选择在甲、乙其中一个直播间进行购物,第一天等可能地从甲、乙两家中选一家直播间购物,如果第一天去甲直播间购物,那么第二天去甲直播间购物的概率为;如果第一天去乙直播间购物,那么第二天去甲直播间购物的概率为 , 求小李第二天去乙直播间购物的概率.参考公式: , 其中 .
临界值表:
-
16、甲乙两位同学进行乒乓球单打比赛,约定:①每赢一球得1分;②采用两球换发制,即每比赛二球交换发球权.假设甲发球时甲得分的概率是 , 乙发球时甲得分的概率是 , 各球的结果相互独立.根据抽签结果决定,甲先发球.(1)、求比赛二球后甲得分的期望;(2)、求比赛六球后甲得分比乙得分多分的概率.
-
17、已知的展开式中,各项系数之和比它的二项式系数之和大992,(1)、求展开式中二项式系数最大的项;(2)、求展开式中有理项.
-
18、为培养学生对传统文化的兴趣,某市从甲,乙两所学校各抽取100名学生参加传统文化知识竞赛,竞赛成绩分为优秀和非优秀两个等级,成绩统计如下表:
优秀人数
非优秀人数
合计
甲校
60
40
100
乙校
70
30
100
合计
130
70
200
(1)甲,乙两所学校竞赛成绩优秀的频率分别是多少?
(2)能否有95%的把握认为甲校成绩优秀与乙校成绩优秀有差异?
附:
P
0.050
0.010
0.001
k
3.841
6.635
10.828
-
19、已知集合 , 对它的非空子集 , 将中每个元素都乘以再求和,如 , 可以求得和为 , 则对的所有非空子集,则这些和的总和为 .
-
20、已知为正数,的展开式中各项系数的和为1,则常数项为.