版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、某同学参加学校组织的数学知识竞赛，在5道四选一的单选题中有3道有思路，有2道完全没有思路，有思路的题目每道做对的概率为 $\frac{1}{2}$ ，没有思路的题目只好任意猜一个答案．若从这5道题目中任选2题，则该同学2道题目都做对的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{7}{32}$ C、 $\frac{3}{16}$ D、 $\frac{5}{32}$

查看解析
2、抛物线有如下光学性质：平行于抛物线对称轴的光线，经过抛物线上的一点反射后，反射光线经过抛物线的焦点．过点 $P (2 \sqrt{2}, 5)$ 且平行于 $y$ 轴的一条光线射向抛物线 $C : x^{2} = 4 y$ 上的 $A$ 点，经过反射后的反射光线与 $C$ 相交于点 $B$ ，则 $|A B| =$ （）

A、 $\frac{7}{2}$ B、9 C、36 D、 $\frac{9}{2}$

查看解析
3、若 $cos (α + \frac{π}{4}) = \frac{3}{5}$ ，则 $sin 2 α =$ （）

A、 $\frac{7}{25}$ B、 $- \frac{7}{25}$ C、 $\frac{9}{25}$ D、 $- \frac{9}{25}$

查看解析
4、已知集合 $A = \{1, 3, 4\}$ ，集合 $B = \{2, 3, 4, 6\}$ ，则如图中的阴影部分表示（）

A、 $\{3, 4\}$ B、 $\{1\}$ C、 $\{2, 6\}$ D、 $\{1, 2, 3, 4, 6\}$

查看解析
5、已知函数 $f (x) = (1 - a x) e^{x} (a \in R)$ .

(1)、讨论 $f (x)$ 的单调性；

(2)、若关于 $x$ 的不等式 $f (x) > a (1 - x)$ 无整数解，求 $a$ 的取值范围.

查看解析
6、欧几里得生活的时期人们就发现了椭圆有如下的光学性质：由椭圆一焦点射出的光线经椭圆内壁反射后必经过另一焦点 $.$ 现有一椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ，长轴长为 $4$ ，从一个焦点 $F$ 发出的一条光线经椭圆内壁上一点 $P$ 反射之后恰好与 $x$ 轴垂直，且 $P F = \frac{7}{2}$ ．

(1)、求椭圆 $C$ 的标准方程；

(2)、已知 $A$ 为该椭圆的左顶点，若斜率为 $k$ 且不经过点 $A$ 的直线 $l$ 与椭圆 $C$ 交于 $M$ ， $N$ 两点，记直线 $A M$ ， $A N$ 的斜率分别为 $k_{1} ， k_{2}$ ，且满足 $k (k_{1} + k_{2}) = 2$ ．
①证明：直线 $l$ 过定点；
②若 $|O M |^{2} +| O N |^{2} = 5$ ，求 $k$ 的值．

查看解析
7、如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A A_{1} ⊥ A_{1} B_{1}$ ， $A B ⊥ B C$ ，四边形 $B C C_{1} B_{1}$ 是菱形．

(1)、证明： $A C_{1} ⊥ B_{1} C$ ；

(2)、若 $A B = B C = \frac{\sqrt{3}}{3} B_{1} C$ ，求二面角 $B - A C_{1} - C$ 的正弦值．

查看解析
8、某大型公司进行了新员工的招聘，共有10000人参与.招聘规则为：前两关中的每一关最多可参与两次测试，只要有一次通过，就自动进入下一关的测试，否则过关失败.若连续通过三关且第三关一次性通过，则成功竞聘，已知各关通过与否相互独立.

(1)、若小李在第一关､第二关及第三关通过测试的概率分别为 $\frac{5}{6}, \frac{4}{5}, \frac{3}{4}$ ，求小李成功竞聘的概率 $P$ ；

(2)、统计得10000名竞聘者的得分 $X \sim N (420.5, {10.75}^{2})$ ，试估计得分在442分以上的竞聘者有多少人.（四舍五人取整）
附：若随机变量 $X \sim N (μ, σ^{2})$ ，则 $P (μ - σ \leq X \leq μ + σ) \approx 0.6827, P (μ - 2 σ \leq X \leq μ + 2 σ) \approx 0.9545$

查看解析
9、在 $△ A B C$ 中， $a cos C + c cos A = \frac{2 \sqrt{3}}{3} b cos B$ .

(1)、求 $∠ B$ ；

(2)、若 $a = 12, D$ 为 $B C$ 边的中点，且 $A D = 3$ ，求 $b$ 的值.

查看解析
10、某零食生产厂家准备用长为 $2 \sqrt{7} cm$ ，宽为4cm的长方形纸板剪去阴影部分（如图，阴影部分是全等四边形），再将剩余部分折成一个底面为长方形的四棱锥形状的包装盒，则该包装盒容积的最大值为 ${cm}^{3}$ .

查看解析
11、已知 $a = {log}_{2} 5$ ， $b = {log}_{3} 11$ ， $c = \frac{5}{2}$ ，则 $a$ ， $b$ ， $c$ 的大小关系是.（用“ $>$ ”连接）

查看解析
12、下列选项正确的是（）

A、命题“ $\exists x > 0$ ， $x^{2} + x + 1 \geq 0$ ”的否定是 $\forall x < 0$ ， $x^{2} + x + 1 < 0$ B、满足 $\{1\} \subseteq M \subseteq \{1, 2, 3\}$ 的集合M的个数为 $4$ C、已知 $x = \lg 3$ ， $y = \lg 5$ ，则 $\lg 45 = 2 x + y$ D、已知指数函数 $f (x) = a^{x}$ （ $a > 0$ 且 $a \neq 1$ ）的图象过点 $(2, 4)$ ，则 $\log_{a} \sqrt{2} = 1$

查看解析
13、已知函数 $f (x)$ 是定义域为 $R$ 且周期为4的奇函数，当 $x \in [0, 2]$ 时， $f (x) = - x^{2} + 2 x$ ， $g (x) = f (x) + f (x + 1)$ ，则下列结论错误的是（）

A、 $f (\frac{4}{11}) + f (\frac{8}{11}) + \dots + f (\frac{40}{11}) + f (4) = 0$ B、函数 $g (x)$ 的图象关于 $x = \frac{5}{2}$ 对称 C、 $g (x)$ 的最大值为 $\frac{3}{2}$ D、函数 $y = g (x) - \frac{1}{6} x$ 有8个零点

查看解析
14、平面向量 $\vec{a} = (1, 2)$ ， $\vec{b} = (4, 2)$ ， $\vec{c} = m \vec{a} + \vec{b}$ （ $m \in R$ ），且 $\vec{c}$ 与 $\vec{a}$ 的夹角等于 $\vec{c}$ 与 $\vec{b}$ 的夹角，则 $m =$ （）

A、 $- 2$ B、 $- 1$ C、 $1$ D、 $2$

查看解析
15、已知 $\log_{\frac{1}{3}} (a - 1) < \log_{\frac{1}{3}} (b - 1)$ ，则下列说法一定成立的是（）

A、 $\frac{1}{a} > \frac{1}{b}$ B、 ${(\frac{1}{2022})}^{a} < {(\frac{1}{2021})}^{b}$ C、 $\ln (a - b) > 0$ D、若 $\vec{A C} = a b \vec{A B}$ ，则点C在线段 $A B$ 上

查看解析
16、为维护市场秩序，保护消费者权益，在“五一”假期来临之际，我市物价部门对某商品在5家商场的售价 $x$ （元）及其一天的销售量 $y$ （件）进行调查，得到五对数据 $(x_{i}, y_{i}) (i = 1, 2, 3, 4, 5)$ ，经过分析、计算，得 $\bar{x} = 10 ， \bar{y} = 8$ ， $y$ 关于 $x$ 的经验回归方程为 $\hat{y} = - 3 x + \hat{a}$ ，则相应于点 $(9, 10)$ 的残差为（）

A、 $- 1$ B、1 C、 $- 3$ D、3

查看解析
17、党的十九大报告指出，要以创新理念提升农业发展新动力，引领经济发展走向更高形态.为进一步推进农村经济结构调整，某村举办水果观光采摘节，并推出配套乡村游项目现统计了4月份200名游客购买水果的情况，得到如图所示的频率分布直方图：
（1）若将购买金额不低于80元的游客称为“水果达人”，现用分层抽样的方法从样本的“水果达人”中抽取5人，求这5人中消费金额不低于100元的人数；
（2）从（1）中的5人中抽取2人作为幸运客户免费参加山村旅游项目，请列出所有的基本事件，并求2人中至少有1人购买金额不低于100元的概率；
（3）为吸引顾客，该村特推出两种促销方案，
方案一：每满80元可立减8元；
方案二：金额超过50元但又不超过80元的部分打9折，金额超过80元但又不超过100元的部分打8折，金额超过100元的部分打7折.
若水果的价格为11元/千克，某游客要购买10千克，应该选择哪种方案更优惠.

查看解析
18、某机械零件工厂为了检验产品的质量，质检部门随机在生产线上抽取了 $100$ 个零件并称出它们的重量（单位：克）．重量按照 $[495, 505)$ ， $[505, 515)$ ， …， $[535, 545]$ 分组，得到频率分布直方图如图所示．
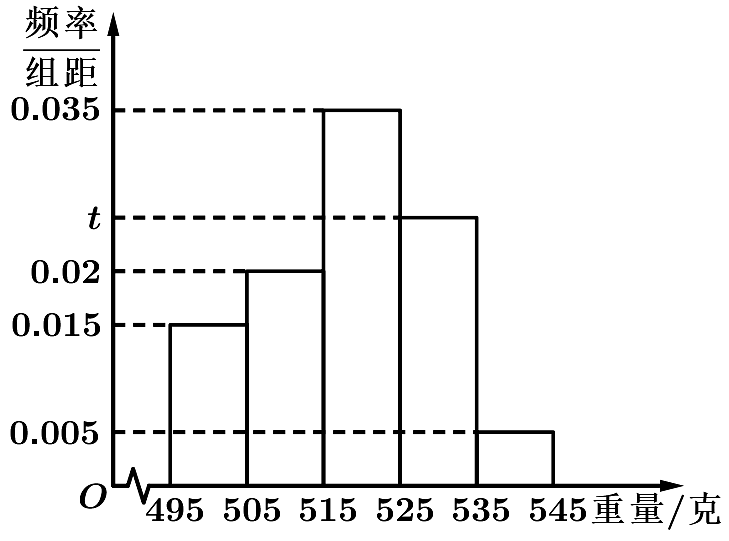
（1）估计该工厂生产的零件重量的平均数；（每组数据用该组的中点值作代表）
（2）估计该工厂生产的零件重量的 $80 %$ 分位数；
（3）按各组零件数量比例用分层随机抽样方法从样本里重量不低于 $525$ 克的零件中抽取 $6$ 个零件，再从这 $6$ 个零件中任取 $2$ 个，求这 $2$ 个零件的重量均在 $[525, 535)$ 内的概率．

查看解析
19、在 $△ A B C$ 中，角 $A, B, C$ 的对边分别为 $a, b, c$ ，且 $cos (A - B) cos B - sin (A - B) sin (A + C) = - \frac{3}{5}$

(1)、求 $sin A$ 的值；

(2)、若 $a = 4 \sqrt{2}, b = 5$ ，求 $△ A B C$ 的面积.

查看解析
20、如图所示，平行四边形 $A B C D$ 的边 $A D$ 所在的直线与菱形 $A B E F$ 所在的平面垂直，且 $G B = G E$ ， $A E = A F$ .
（1）求证：平面 $A C G ⊥$ 平面 $A D F$ ；
（2）若 $A F = 2$ ， ______，求二面角 $C - A G - F$ 的余弦值，从① $B C = \sqrt{2} A B$ ， ② $B C = A G$ 这两个条件中任选一个填入上面的横线上，并解答问题.

查看解析

上一页 594 595 596 597 598 下一页跳转