版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知曲线C的方程为： $\{\begin{array}{l} \frac{x^{2}}{4} + \frac{y^{2}}{3} = 1 (y \geq 0) \\ x^{2} + y^{2} = 4 (y < 0) \end{array}$ ， $M (- 1, 0)$ ， $N (1, 0)$ ，过M的直线交曲线C于A、B两点（A在B的上方），已知 $∠ A M N = α$ ， $∠ A N M = β$ ，下列命题正确的是（）

A、 $\sin α + \sin β = 2 \sin (α + β)$ B、 $\tan \frac{α}{2} + 3 \tan \frac{β}{2}$ 的最小值是2 C、 $△ A B N$ 周长的最大值是 $4 + 2 \sqrt{5}$ D、若 $α = \frac{π}{3}$ ，将 $△ A M N$ 沿 $M N$ 翻折，使面 $A M N ⊥$ 面 $M N B$ ，则折后 $|A B| = \frac{3 + \sqrt{13}}{2}$

查看解析
2、下列说法中正确的是（）

A、数据1，2，2，3，4，5的极差与众数之和为7 B、若随机变量X服从二项分布 $X ~ B (20, p)$ ，且 $E (X) = 8$ ，则 $D (X) = 4.8$ C、X和Y是分类变量，若 $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ 值越大，则判断“X与Y独立”的把握性越大 D、若随机变量X服从正态分布 $X ~ N (2, σ^{2})$ ，且 $P (X > 5) = 0.2$ ，则 $P (- 1 < X < 5) = 0.6$

查看解析
3、已知函数 $f (x) = (a - 2) x^{2} + b x - a + 1$ （a， $b \in R$ 且 $a \neq 2$ ）在区间 $[1, 2]$ 上有零点，则 $a^{2} + b^{2}$ 的最小值为（）

A、 $\frac{3}{2}$ B、 $\frac{1}{2}$ C、2 D、1

查看解析
4、函数 $y = \sin (2 ω x + φ) (ω > 0)$ 的部分图象如图所示，直线 $y = \frac{1}{2}$ 与其交于A，B两点，若 $|A B| = \frac{π}{3}$ ，则 $ω =$ （）

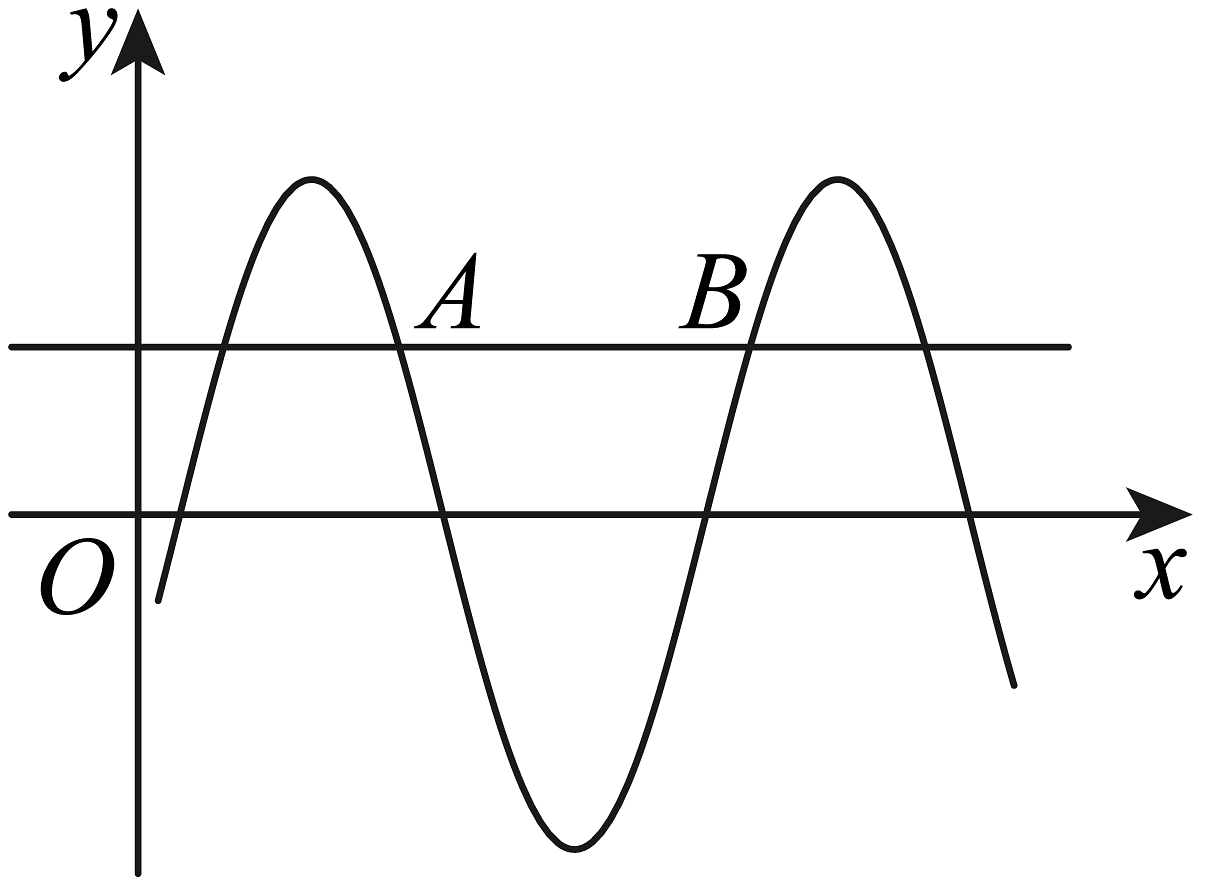A、4 B、3 C、2 D、1

查看解析
5、在 $△ A B C$ 中，D是BC上一点，满足 $\vec{B D} = 2 \vec{D C}$ ， M是AD的中点，若 $\vec{B M} = λ \vec{B A} + μ \vec{B C}$ ，则 $λ + μ =$ （）

A、 $\frac{5}{4}$ B、 $\frac{7}{8}$ C、 $\frac{5}{6}$ D、 $\frac{5}{8}$

查看解析
6、若命题“ $\exists x \in R$ ， $x^{2} + 2 x + a < 0$ 成立”是真命题，则实数a的取值范围是（）

A、 $a \leq 1$ B、 $a < 1$ C、 $a \geq 1$ D、 $a > 1$

查看解析
7、设复数 $z_{1}$ ， $z_{2}$ 在复平面内对应的点关于实轴对称， $z_{1} = 2 - i$ ，则 $\frac{z_{1}}{z_{2}} =$ （）

A、 $\frac{3}{5} - \frac{4}{5} i$ B、 $\frac{3}{5} + \frac{4}{5} i$ C、 $1 + \frac{4}{5} i$ D、 $1 - \frac{4}{5} i$

查看解析
8、已知集合 $A = \{0, - 1\}$ ， $B = \{0, 1, 2 - a\}$ 且 $A \subseteq B$ ，则a等于（）

A、1 B、 $- 1$ C、 $- 3$ D、3

查看解析
9、已知 $A$ 、 $B$ 是椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 长轴的两顶点， $M$ 是椭圆上的一点，直线 $A M$ 与 $B M$ 斜率之积 $k_{A M} \cdot k_{B M} > - \frac{1}{4}$ ，则此椭圆的离心率取值范围是（）

A、 $(\frac{1}{4}, 1)$ B、 $(\frac{1}{2}, 1)$ C、 $(\frac{\sqrt{2}}{2}, 1)$ D、 $(\frac{\sqrt{3}}{2}, 1)$

查看解析
10、已知抛物线 $C : y^{2} = 2 p x (p > 0)$ 的焦点F在直线 $l : y = x - 1$ 上．

(1)、求C的方程；

(2)、过点 $P (0, - 1)$ 的直线交C于M，N两点，又点Q在线段MN上，且 $\frac{|P M|}{|P N|} = \frac{|Q M|}{|Q N|}$ ，证明：点Q在定直线上．

查看解析
11、在四棱锥 $P - A B C D$ 中，底面ABCD是边长为2的正方形，且 $P A = A B$ ， $P A ⊥$ 底面ABCD，点E满足 $2 \vec{P E} = \vec{P C}$ ．

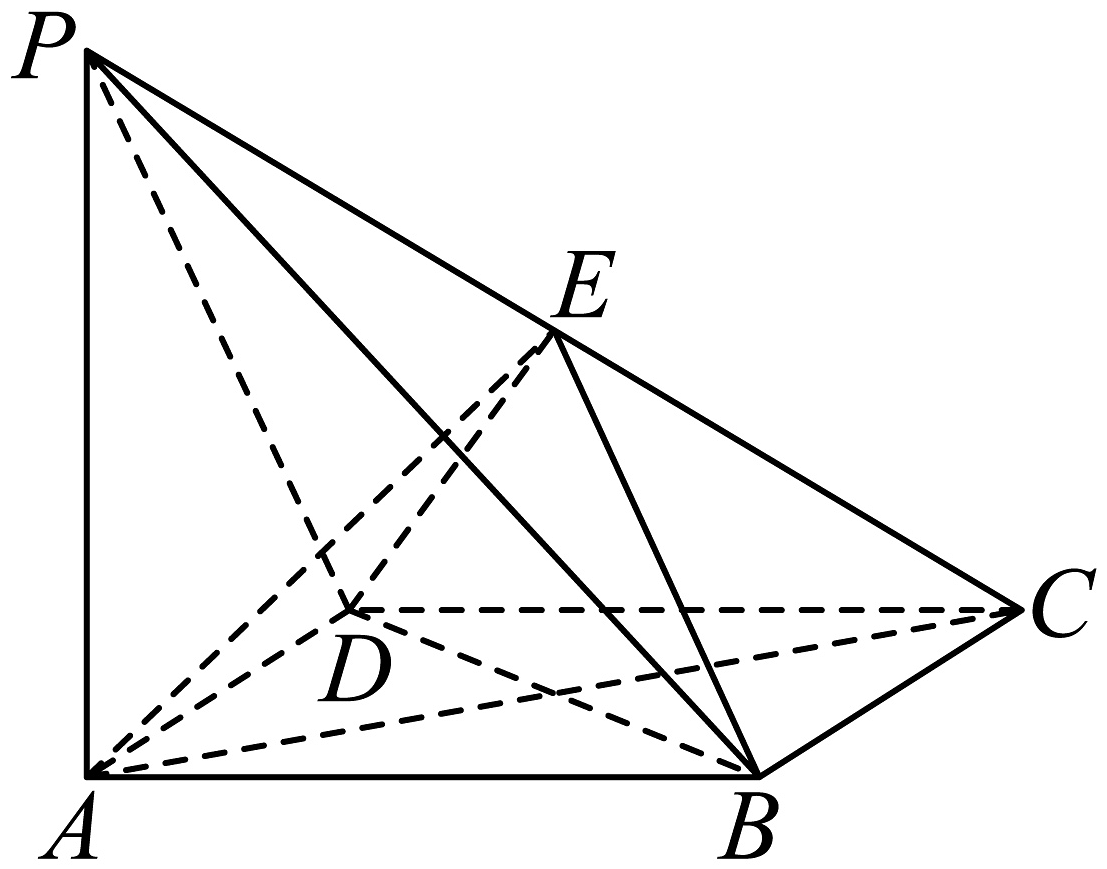(1)、证明： $B D ⊥$ 平面PAC；

(2)、求平面ABE与平面BDE的夹角的大小．

查看解析
12、2024年5月底，各省教育厅陆续召开了2024年高中数学联赛的相关工作，某市经过初次选拔后有小明，小王，小红三名同学成功进入决赛，在决赛环节中三名同学同时解答一道有关组合数论的试题．已知小明成功解出这道题的概率是 $\frac{3}{4}$ ，小明，小红两名同学都解答错误的概率是 $\frac{1}{12}$ ，小王、小红两名同学都成功解出的概率是 $\frac{1}{4}$ ，这三名同学解答是否正确相互独立.

(1)、分别求出小王，小红两名同学成功解出这道题的概率；

(2)、求三人中至少有两人成功解出这道题的概率．

查看解析
13、已知函数 $f (x) = (x + 1) \ln x$ ，记 $f^{'} (x)$ 为 $f (x)$ 的导函数．

(1)、求曲线 $f (x)$ 在点 $(1, f (1))$ 处的切线方程；

(2)、求 $f^{'} (x)$ 的最值．

查看解析
14、某高校的化学实验室内的电子微型质量测量仪的底座形似一个正四棱台，记该正四棱台为 $A B C D - A_{1} B_{1} C_{1} D_{1}$ ，经测量其体积为 $\frac{28 \sqrt{3}}{3}$ ，上底面 $A_{1} B_{1} C_{1} D_{1}$ ，下底面 $A B C D$ 的边长分别为2，4，记 $A C$ ， $B D$ 交于点 $O$ ， $A_{1} C_{1}$ ， $B_{1} D_{1}$ ，交于点 $O_{1}$ ，则 $O A_{1} =$ ，若四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的各个顶点均在球 $O_{2}$ 的表面上，则球 $O_{2}$ 的表面积为.

查看解析
15、若双曲线 $C : x^{2} - \frac{y^{2}}{3} = 1$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ， P是C右支上的动点，则 $|P F_{1}| \cdot |P F_{2}|$ 的最小值为．

查看解析
16、在某次考弍中，某陪考老师记录了12名同学提前到考场的时间（单位：分钟）分别为 $11, 12, 12, 13, 13, 14, 14, 15, 15, 16, 17, 18$ ，则该组数据的上四分位数为.

查看解析
17、已知函数 $f (x) = \{\begin{array}{l} 3 \sin^{2} x - 1, \sin x \geq 0, \\ \sin^{2} x - 1, \sin x < 0, \end{array}$ $x \in (0, 2 π)$ ，若方程 $f (x) = a \pm 1$ 有6个根，则 $a$ 的值可能为（）

A、0 B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看解析
18、已知 $(1 - 2 i) z = 1 + 3 i$ ，则（）

A、 $z = - 1 + i$ B、 $|z| = \sqrt{3}$ C、 $\bar{z}$ 在复平面上对应的点位于第三象限 D、 $z + 3 \bar{z} = - 4 - 2 i$

查看解析
19、已知直线l与圆 $O : x^{2} + y^{2} = 36$ 交于M，N两点，若以MN为直径的圆过点 $P (0, 8)$ ，则 $|M N|$ 的最大值为（）

A、 $4 + 2 \sqrt{2}$ B、 $3 + 2 \sqrt{2}$ C、 $8 + 2 \sqrt{2}$ D、 $4 + \sqrt{2}$

查看解析
20、在△ABC中，内角A，B，C的对边分别为a，b，c，满足 $2 b^{2} + c^{2} - a^{2} = 0$ ，则 $\sin B$ 的最大值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看解析

上一页 592 593 594 595 596 下一页跳转