相关试卷
- 高中数学人教新课标A版必修3 第一章 算法初步 1.3算法案例
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.3循环语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.2.1输入语句、输出语句和赋值语句
- 高中数学人教新课标A版必修3 第一章 算法初步 1.1算法与程序框图(包括1.1.1算法的概念,1.1.2程序框图与算法的基本逻辑结构)
- 高中数学人教新课标A版必修3 第三章 概率 3.3几何概型
- 高中数学人教新课标A版必修3 第三章 概率 3.2古典概型
- 高中数学人教新课标A版 必修3 第三章 概率 3.1.3概率的基本性质
- 高中数学人教新课标A版必修3 第三章 概率 3.1.1随机事件的概率,3.1.2概率的意义
- 高中数学人教新课标A版必修3 第二章 统计 2.3变量间的相关关系(包括2.3.1变量间的相关关系,2.3.2两个变量的线性相关)
- 高中数学人教新课标A版必修3 第二章 统计 2.2.2用样本的数字特征估计总体的数字特征
-
1、已知函数为奇函数,为偶函数,且当时, , 则( )A、2 B、-2 C、1 D、-1
-
2、已知点O为的外心,且向量 , , 若向量在向量上的投影向量为 , 则的值为( )A、 B、 C、 D、
-
3、在平行四边形中, , , , 是的中点,沿将翻折至的位置,使得平面平面 , 为的中点,则异面直线与所成角的余弦值为( )
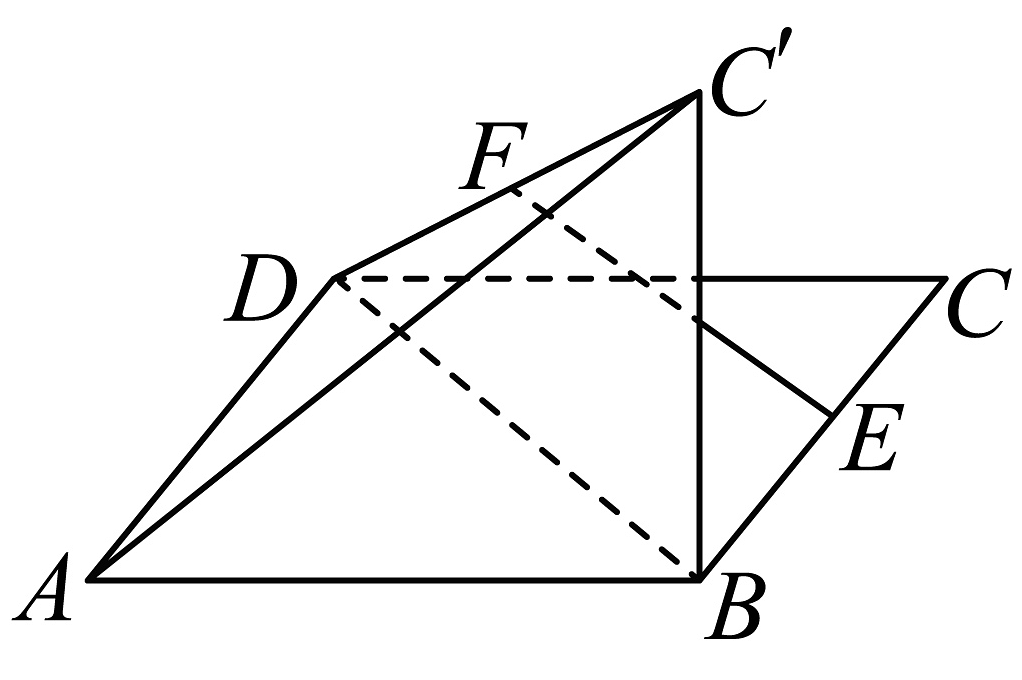 A、 B、 C、 D、
A、 B、 C、 D、 -
4、飞行棋是大家熟悉的棋类游戏,玩家通过投掷骰子来决定飞机起飞与飞行的步数.当且仅当玩家投掷出点时,飞机才能起飞.并且掷得点的游戏者可以连续投掷骰子,直至显示点数不是点.飞机起飞后,飞行步数即骰子向上的点数.(1)、求甲玩家第一轮投掷中,投郑次数的均值)(2)、对于两个离散型随机变量、 , 我们将其可能出现的结果作为一个有序数对,类似于离散型随机变量的分布列,我们可以用如下表格来表示这个有序数对的概率分布:
(记 , )
若已知 , 则事件的条件概率为.可以发现依然是一个随机变量,可以对其求期望.
(ⅰ)上述期望依旧是一个随机变量(取值不同时,期望也不同),不妨记为 , 求;
(ⅱ)若修改游戏规则,需连续掷出两次点飞机才能起飞,记表示“甲第一次未能掷出6点”,表示“甲第一次掷出点且第二次未能掷出点”,表示“甲第一次第二次均掷出点”,为甲首次使得飞机起飞时抛掷骰子的次数,求.
-
5、下列命题正确的有( )A、已知函数在上可导,若 , 则 B、已知函数 , 若 , 则 C、 D、设函数的导函数为 , 且 , 则
-
6、在中, , 为外心,且 , 则的最大值为( )A、 B、 C、 D、
-
7、在如图所示的试验装置中,两个正方形框架 , 的边长都是1,且它们所在平面互相垂直,活动弹子分别在正方形对角线和上移动,且和的长度保持相等,记 , 活动弹子在上移动.
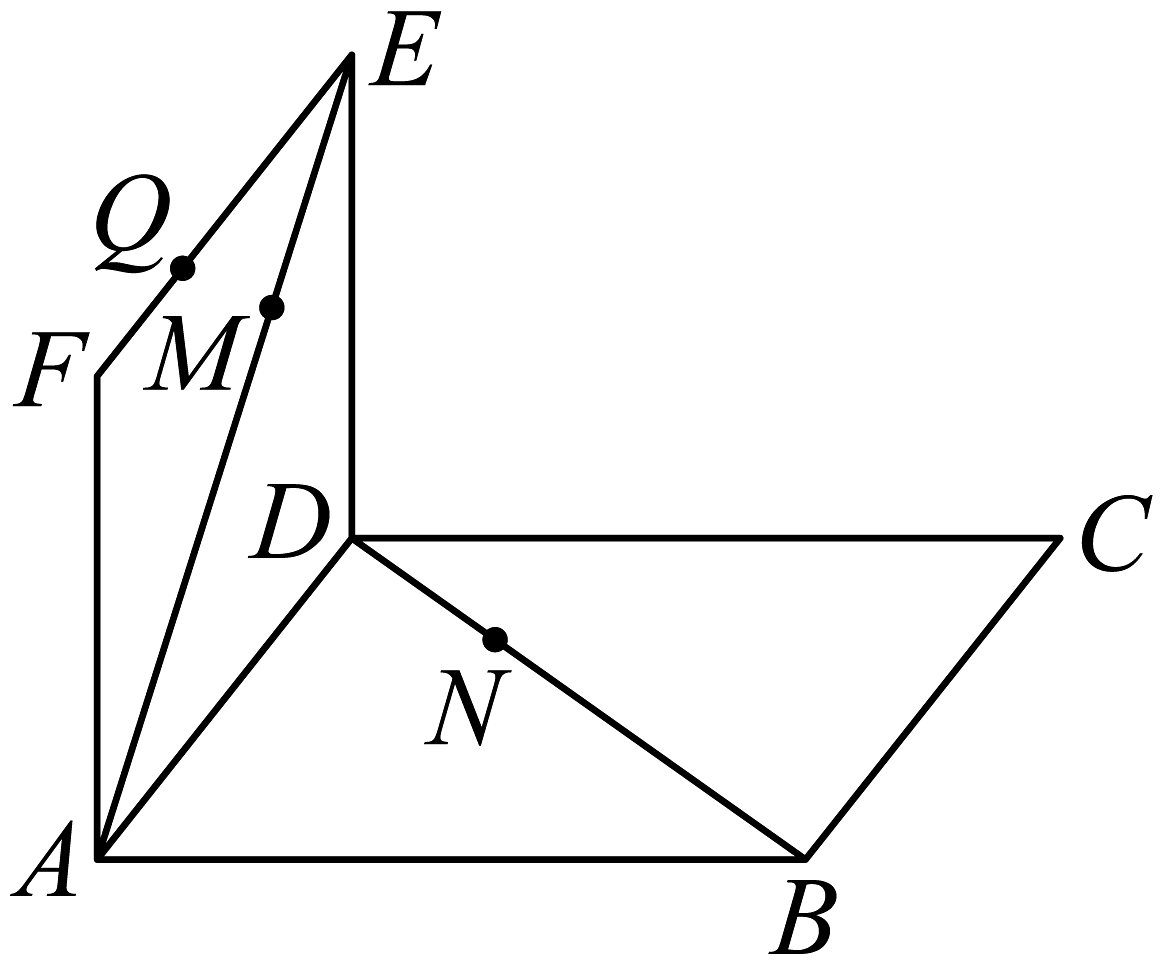 (1)、求证:直线平面;(2)、为上的点,求与平面所成角的正弦值的最大值.
(1)、求证:直线平面;(2)、为上的点,求与平面所成角的正弦值的最大值. -
8、质量监督局检测某种产品的三个质量指标 , 用综合指标核定该产品的等级.若 , 则核定该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号
质量指标()
产品编号
质量指标()
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品的一等品中,随机抽取2件产品,设事件为“在取出的2件产品中,每件产品的综合指标均满足”,求事件的概率.
-
9、直线l经过两直线:和:的交点.(1)、若直线l与直线垂直,求直线l的方程;(2)、若点到直线l的距离为5,求直线l的方程.
-
10、在空间直角坐标系中,已知向量 , 点 , 点 , 若平面经过点 , 且以为法向量,是平面内的任意一点,则平面的方程为:.由以上的理论,已知一平面和直线垂直,为其垂足,若 , 平面的方程式是
-
11、已知 , 从点射出的光线经x轴反射到直线上,又经过直线反射回到时点,则光线所经过的路程为 .
-
12、如图是一个古典概型的样本空间和事件和事件 , 其中 , , , , 那么

-
13、直线与圆C:相交所形成的弦中长度最短的弦长为
-
14、直线上的一点 , 到与的距离之差的绝对值的最大值为.
-
15、已知点A(1,2)在圆C:外,则实数m的取值范围为.
-
16、若直线与曲线有公共点,则的取值范围是( )A、 B、 C、 D、
-
17、已知直线 , 若直线与连接、两点的线段总有公共点,则直线的斜率的范围为( )A、 B、 C、 D、
-
18、在一个盒子中有3个红球和2个黑球,这5个球除颜色外没有其他差异.现从中依次不放回地随机抽取出2个球.则两次取到的球颜色相同的概率为( )A、 B、 C、 D、
-
19、正三棱柱各棱长均为 , 为的中点,那么四面体 的体积( )A、 B、 C、 D、
-
20、函数的图象与函数的图象关于轴对称,则( )A、 B、 C、 D、