版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知复数 $z = \frac{2 - i}{1 + i}$ ，则复数 $z$ 的虚部为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{2} i$ C、 $- \frac{3}{2}$ D、 $- \frac{3}{2} i$

查看解析
2、设 $\vec{a}, \vec{b}$ 均为单位向量，且 $\vec{a} \cdot \vec{b} = \frac{1}{4}$ ，则 $|\vec{a} + 2 \vec{b}| =$ （）

A、 $3$ B、 $\sqrt{6}$ C、 $6$ D、 $9$

查看解析
3、已知函数 $f (x) = \frac{1}{x} - x + 2 a \ln x$ （其中 $a$ 是实数）.
（1）若 $a = \frac{1}{2}$ ，求曲线 $y = f (x)$ 在 $(1, f (1))$ 处的切线方程；
（2）求函数 $f (x)$ 的单调区间；
（3）设 $g (x) = \ln x - b x - c x^{2}$ ，若函数 $f (x)$ 的两个极值点 $x_{1}, x_{2} (x_{1} < x_{2})$ 恰为函数 $g (x)$ 的两个零点，且 $y = (x_{1} - x_{2}) g^{'} (\frac{x_{1} + x_{2}}{2})$ 的范围是 $[\ln 2 - \frac{2}{3}, + \infty)$ ，求实数 $a$ 的取值范围.

查看解析
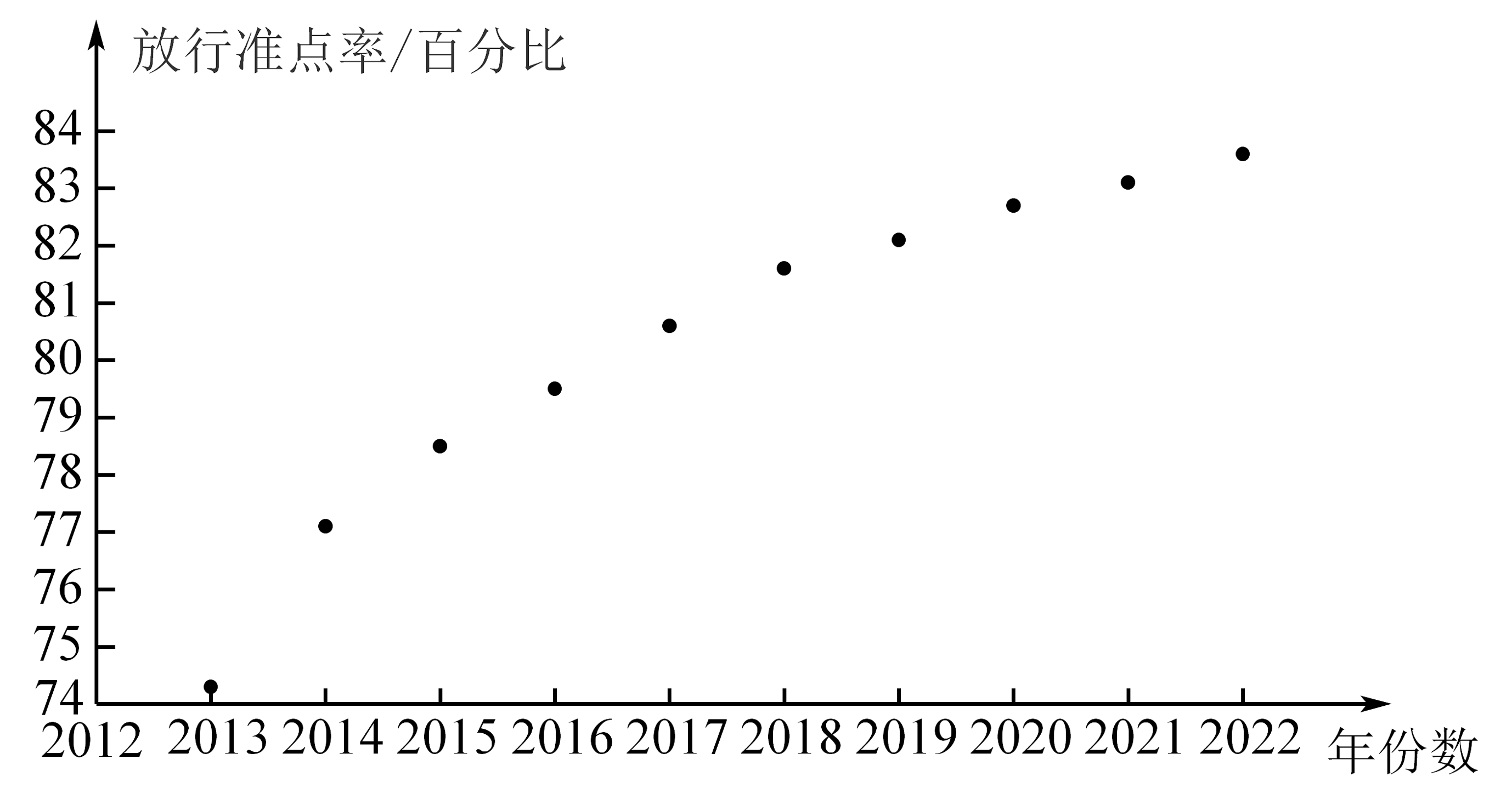
4、放行准点率是衡量机场运行效率和服务质量的重要指标之一.某机场自2012年起采取相关策略优化各个服务环节，运行效率不断提升.以下是根据近10年年份数 $x_{i}$ 与该机场飞往A地航班放行准点率 $y_{i}$ （ $i = 1 ， 2 ， \dots ， 10$ ）（单位：百分比）的统计数据所作的散点图及经过初步处理后得到的一些统计量的值.
$\bar{x}$
$\bar{y}$
$\bar{t}$
$\sum_{i = 1}^{10} x_{i}^{2}$
$\sum_{i = 1}^{10} x_{i} y_{i}$
$\sum_{i = 1}^{10} t_{i}^{2}$
$\sum_{i = 1}^{10} t_{i} y_{i}$
2017.5
80.4
1.5
40703145.0
1621254.2
27.7
1226.8
其中 $t_{i} = \ln (x_{i} - 2012)$ ， $\bar{t} = \frac{1}{10} \sum_{i = 1}^{10} t_{i}$

(1)、根据散点图判断， $y = b x + a$ 与 $y = c \ln (x - 2012) + d$ 哪一个适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型（给出判断即可，不必说明理由），并根据表中数据建立经验回归方程，由此预测2023年该机场飞往A地的航班放行准点率.

(2)、已知2023年该机场飞往A地､B地和其他地区的航班比例分别为0.2、0.2和0.6.若以（1）中的预测值作为2023年该机场飞往A地航班放行准点率的估计值，且2023年该机场飞往B地及其他地区（不包含A、B两地）航班放行准点率的估计值分别为 $80 %$ 和 $75 %$ ，试解决以下问题：
（i）现从2023年在该机场起飞的航班中随机抽取一个，求该航班准点放行的概率；
（ii）若2023年某航班在该机场准点放行，判断该航班飞往A地、B地、其他地区等三种情况中的哪种情况的可能性最大，说明你的理由.
附：（1）对于一组数据 $(u_{1}, v_{1})$ ， $(u_{2}, v_{2})$ ， …， $(u_{n}, v_{n})$ ，其回归直线 $v = α + β u$ 的斜率和截距的最小二乘估计分别为 $\hat{β} = \frac{\sum_{i = 1}^{n} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(u_{i} - \bar{u})}^{2}} = \frac{\sum_{i = 1}^{n} u_{i} v_{i} - n \bar{u} \cdot \bar{v}}{\sum_{i = 1}^{n} u_{i}^{2} - n {\bar{u}}^{2}}$ ， $\hat{α} = \bar{v} - \hat{β} \bar{u}$
参考数据： $\ln 10 \approx 2.30$ ， $\ln 11 \approx 2.40$ ， $\ln 12 \approx 2.48$ .

查看解析
5、已知 $f (x) = {(2 x - 3)}^{n}$ 展开式的二项式系数和为512，且 ${(2 x - 3)}^{n} = a_{0} + a_{1} (x - 1) + a_{2} {(x - 1)}^{2} + \dots + a_{n} {(x - 1)}^{n}$ .

(1)、求 $a_{3}$ 的值；

(2)、求 $a_{1} + a_{2} + a_{3} + \dots + a_{n}$ 的值；

(3)、求 $f (6) - 6$ 被8整除的余数.

查看解析
6、已知等比数列 $\{a_{n}\}$ 的首项 $a_{1} = 1$ ，公比为 $q$ ，前 $n$ 项和为 $S_{n}$ ，且 $S_{4}$ ， $S_{3}$ ， $S_{5}$ 成等差数列.

(1)、求 $\{a_{n}\}$ 的通项 $a_{n}$ ；

(2)、若 $b_{n} = \{\begin{cases} a_{n}, n = 2 k - 1 \\ q n + 1, n = 2 k \end{cases}, k \in N^{*}$ ，求 $\{b_{n}\}$ 的前 $n$ 项和 $T_{n}$ .

查看解析
7、对于三次函数 $f (x) = a x^{3} + b x^{2} + c x + d (a \neq 0)$ ，给出定义：设 $f^{'} (x)$ 是函数 $y = f (x)$ 的导数， $f^{″} (x)$ 是函数 $f^{'} (x)$ 的导数，若方程 $f^{″} (x) = 0$ 有实数解 $x_{0}$ ，则称点 $(x_{0}, f (x_{0}))$ 为函数 $y = f (x)$ 的“拐点”.某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心.给定函数 $f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} + 3 x - \frac{5}{12}$ ，请你根据上面的探究结果，解答以下问题：
①函数 $f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} + 3 x - \frac{5}{12}$ 的对称中心坐标为；
②计算 $f (\frac{1}{2024}) + f (\frac{2}{2024}) + f (\frac{3}{2024}) + \dots + f (\frac{2023}{2024}) =$ .

查看解析
8、已知 $(x + \frac{1}{x}) {(2 x - 1)}^{5}$ 的展开式中含 $x^{3}$ 的项的系数为.

查看解析
9、从1，2，3，6，9中任取两个不同的数相乘，则不同的乘积结果有种，乘积为偶数的取法有种.

查看解析
10、有甲、乙两个小组参加某项测试，甲组的合格率为70%，乙组的合格率为90%．已知甲、乙两组的人数分别占这两组总人数的70%，30%．从这两组组成的总体中任选一个人，用事件 $A_{1}$ ， $A_{2}$ 分别表示选取的该人来自甲、乙组，事件 $B$ 表示选取的该人测试合格，则（）

A、 $P (A_{1} B) = 0.49$ B、 $P (B| A_{1}) = 0.9$ C、 $P (A_{2} B) = 0.21$ D、 $P (B) = 0.76$

查看解析
11、甲、乙、丙、丁、戊五人并排站成一排，下列说法正确的是（）

A、如果甲、乙必须相邻，那么不同的排法有24种 B、最左端只能排甲或乙，最右端不能排甲，则不同的排法共有42种 C、甲、乙不相邻的排法种数为72种 D、甲在乙左边的排列的排法有30种

查看解析
12、 $\forall x_{1}$ ， $x_{2} \in [1, e]$ ，当 $x_{1} < x_{2}$ 时，都有 $\ln \frac{x_{1}}{x_{2}} > a (x_{1} - x_{2})$ ，则实数 $a$ 的最小值为（）

A、 $\frac{1}{e^{2}}$ B、 $\frac{1}{e}$ C、 $\frac{\sqrt{e}}{e}$ D、1

查看解析
13、已知 $f (x)$ 的定义域为 $(0, + \infty)$ ， $f^{'} (x)$ 为 $f (x)$ 的导函数，且满足 $f (x) < - x f^{'} (x)$ ，则不等式 $f (x + 1) > (x - 1) f (x^{2} - 1)$ 的解集是（）

A、 $(0, 1)$ B、 $(2, + \infty)$ C、 $(1, 2)$ D、 $(1, + \infty)$

查看解析
14、已知在8个电子元件中，有2个次品，6个合格品，每次任取一个测试，测试完后不再放回，直到2个次品都找到为止，则经过3次测试恰好将2个次品全部找出的概率为（）

A、 $\frac{1}{14}$ B、 $\frac{3}{56}$ C、 $\frac{1}{42}$ D、 $\frac{4}{21}$

查看解析
15、为了研究经常使用手机是否对数学学习成绩有影响，某校高二数学研究性学习小组进行了调查，随机抽取高二年级50名学生的一次数学单元测试成绩，并制成下面的2×2列联表：
使用手机情况
成绩
合计
及格
不及格
很少
20
5
25
经常
10
15
25
合计
30
20
50
参考公式： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .
附表：
$α$
0.05
0.025
0.010
0.005
0.001
$x_{α}$
3.841
5.024
6.635
7.879
10.828
参照附表，得到的正确结论是（）

A、依据小概率值 $α = 0.01$ 的独立性检验，认为“经常使用手机与数学学习成绩无关” B、依据小概率值 $α = 0.001$ 的独立性检验，认为“经常使用手机与数学学习成绩有关” C、在犯错误的概率不超过0.5%的前提下，认为“经常使用手机与数学学习成绩无关” D、在犯错误的概率不超过0.5%的前提下，认为“经常使用手机与数学学习成绩有关”

查看解析
16、已知离散型随机变量 $ξ$ 的概率分布列如下表：则数学期望 $E (ξ)$ 等于（）
$ξ$
$1$
$3$
$5$
$P$
$0.5$
$m$
$0.2$

A、 $1$ B、 $0.6$ C、 $2 + 3 m$ D、 $2.4$

查看解析
17、在等差数列 $\{a_{n}\}$ 中，若 $a_{4} + a_{6} = 10, a_{7} = 9$ ，则公差 $d =$ （）

A、1 B、2 C、3 D、4

查看解析
18、某高一数学研究小组，在研究边长为1的正方形 $A B C D$ 某些问题时，发现可以在不作辅助线的情况下，用高中所学知识解决或验证下列有趣的现象．若 $P, Q$ 分别为边 $A B, D A$ 上的动点，当 $△ A P Q$ 的周长为2时， $P Q$ 有最小值（图1）、 $∠ P C Q$ 为定值（图2）、 $C$ 到 $P Q$ 的距离为定值（图3）．请你分别解以上问题．

(1)、如图1，求 $P Q$ 的最小值；

(2)、如图2，证明： $∠ P C Q$ 为定值；

(3)、如图3，证明： $C$ 到 $P Q$ 的距离为定值．

查看解析
19、在 $△ A B C$ 中， $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ ．

(1)、证明： $G$ 为 $△ A B C$ 的重心．

(2)、若 $A G = 4, B C = 6$ ，求 $B G + \sqrt{3} C G$ 的最大值，并求此时 $A B$ 的长．

查看解析
20、“熵”常用来判断系统中信息含量的多少，也用来判断概率分布中随机变量的不确定性大小，一般熵越大表示随机变量的不确定性越明显．定义：随机变量 $X$ 对应取值 $x_{i}$ 的概率为 $p_{i} = P (X = x_{i})$ ，其单位为bit的熵为 $H (X) = - \sum_{i = 1}^{n} p_{i} \log_{2} p_{i}$ ，且 $\sum_{i = 1}^{n} p_{i} = 1$ ．（当 $p_{i} = 0$ ，规定 $p_{i} {log}_{2} p_{i} = 0$ ．）

(1)、若抛掷一枚硬币1次，正面向上的概率为 $m (0 < m < 1)$ ，正面向上的次数为 $X$ ，分别比较 $m = \frac{1}{2}$ 与 $m = \frac{1}{4}$ 时对应 $H (X)$ 的大小，并根据你的理解说明结论的实际含义；

(2)、若拋掷一枚质地均匀的硬币 $n$ 次，设 $X$ 表示正面向上的总次数， $Y$ 表示第 $n$ 次反面向上的次数（0或1）． $p (x_{1}, y_{1})$ 表示正面向上 $x_{1}$ 次且第 $n$ 次反面向上 $y_{1}$ 次的概率，如 $n = 3$ 时， $p (0, 1) = \frac{1}{8}$ ．对于两个离散的随机变量 $X, Y$ ，其单位为bit的联合熵记为 $H (X, Y) = - (\sum_{i = 1}^{n} p (x_{i}, 0) \log_{2} p (x_{i}, 0) + \sum_{i = 1}^{n} p (x_{i}, 1) \log_{2} p (x_{i}, 1))$ ，且 $\sum_{i = 1}^{n} p (x_{i}, 0) + \sum_{i = 1}^{n} p (x_{i}, 1) = 1$ ．
（ⅰ）当 $n = 3$ 时，求 $H (X, Y)$ 的值；
（ⅱ）求证： $H (X, Y) < n - \frac{1}{2^{n - 1}} (n \geq 3)$ ．

查看解析

上一页 1309 1310 1311 1312 1313 下一页跳转

$\bar{x}$	$\bar{y}$	$\bar{t}$	$\sum_{i = 1}^{10} x_{i}^{2}$	$\sum_{i = 1}^{10} x_{i} y_{i}$	$\sum_{i = 1}^{10} t_{i}^{2}$	$\sum_{i = 1}^{10} t_{i} y_{i}$
2017.5	80.4	1.5	40703145.0	1621254.2	27.7	1226.8

使用手机情况	成绩		合计
使用手机情况	及格	不及格	合计
很少	20	5	25
经常	10	15	25
合计	30	20	50

$α$	0.05	0.025	0.010	0.005	0.001
$x_{α}$	3.841	5.024	6.635	7.879	10.828

$ξ$	$1$	$3$	$5$
$P$	$0.5$	$m$	$0.2$