河北省承德市2016-2017学年高一下学期数学期末考试试卷

试卷更新日期：2017-11-23 类型：期末考试

进入出卷网下载

一、选择题

1. 数列{a_n}满足a₁=1，a_n₊₁=3a_n（n∈N^*），则a₅等于（）

A、27 B、﹣27 C、81 D、﹣81

查看试题解析
2. 直线 $\frac{x}{3}$ ﹣ $\frac{y}{4}$ =1在x轴上的截距是（）

A、﹣3 B、3 C、﹣4 D、4

查看试题解析
3. 已知a，b是两条直线，α是一个平面，则下列判断正确的是（）

A、a⊥α，b⊥α，则a⊥b B、a∥α，b⊂α，则a∥b C、a⊥b，b⊂α，则a⊥α D、a∥b，b⊂α，a⊄α，则a∥α

查看试题解析
4. 已知x＜0，﹣2＜y＜﹣1，则下列结论正确的是（）

A、xy＞x＞xy² B、xy²＞xy＞x C、xy＞xy²＞x D、x＞xy＞xy²

查看试题解析
5. 已知{a_n}为等差数列，其前n项和为S_n ，若a₃=6，S₃=12，则公差d等于（）

A、1 B、 $\frac{5}{3}$ C、2 D、3

查看试题解析
6. 在△ABC中，角A，B，C的对边分别是a，b，c，若C=45°，c= $\sqrt{2}$ a，则A等于（）

A、120° B、60° C、150° D、30°

查看试题解析
7. 如图是一个几何体的三视图，则该几何体的表面积为（）

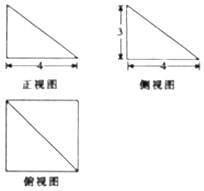A、46 B、48 C、50 D、52

查看试题解析
8. 直线（2a+5）x﹣y+4=0与2x+（a﹣2）y﹣1=0互相垂直，则a的值是（）

A、﹣4 B、4 C、3 D、﹣3

查看试题解析
9. 已知变量x，y满足约束条件 ${\begin{matrix} - 2 x + y \leq 4 \\ 4 x + 3 y \leq 12 \\ y \geq 1 \end{matrix}$ ，则z=2x+y的最小值为（）

A、 $- \frac{1}{2}$ B、1 C、﹣2 D、 $\frac{11}{2}$

查看试题解析
10. 飞机的航线和山顶在同一个铅垂直平面内，已知飞机的高度为海拔15000m，速度为1000km/h，飞行员先看到山顶的俯角为18°，经过108s后又看到山顶的俯角为78°，则山顶的海拔高度为（）

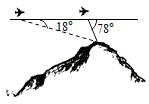A、（15﹣18 $\sqrt{3}$ sin18°cos78°）km B、（15﹣18 $\sqrt{3}$ sin18°sin78°）km C、（15﹣20 $\sqrt{3}$ sin18°cos78°）km D、（15﹣20 $\sqrt{3}$ sin18°sin78°）km

查看试题解析
11. 在四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD为矩形，AB=2BC，E是CD上一点，若AE⊥平面PBD，则 $\frac{C E}{E D}$ 的值为（）

A、 $\frac{3}{2}$ B、 $\frac{5}{2}$ C、3 D、4

查看试题解析
12. 已知数列{a_n}中，a₁=2，当n≥2时， $\frac{a_{n}}{2^{n}}$ = $\frac{a_{n - 1}}{2^{n - 1}}$ +n﹣1，设b_n= $\frac{a_{n}}{2^{n}}$ ﹣1，则 $\frac{1}{b_{2}}$ + $\frac{1}{b_{3}}$ +…+ $\frac{1}{b_{20}}$ 等于（）

A、 $\frac{19}{10}$ B、 $\frac{29}{20}$ C、 $\frac{40}{21}$ D、 $\frac{36}{19}$

查看试题解析

二、填空题

13. 如果直线4ax+y+2=0与直线（1﹣3a）x+ay﹣2=0平行，那么a等于．

查看试题解析
14. 底面半径为2 $\sqrt{3}$ ，母线长为4的圆锥的体积为．

查看试题解析
15. 在△ABC中，角A，B，C的对边分别为a，b，c，asinB= $\sqrt{2}$ sinC，sinC= $\frac{2 \sqrt{2}}{3}$ ，△ABC的面积为4，则c= ．

查看试题解析
16. 已知三棱锥P﹣ABC的四个顶点都在球O的球面上，△ABC是边长为2 $\sqrt{3}$ 的正三角形，PA⊥平面ABC，若三棱锥P﹣ABC的体积为2 $\sqrt{3}$ ，则球O的表面积为．

查看试题解析

三、解答题

17. 设函数f（x）=ax²+（b﹣1）x+3．

(1)、若不等式f（x）＞0的解为（﹣1， $\frac{3}{2}$ ），求不等式bx²﹣3x+a≤0的解集；

(2)、若f（1）=4，a＞0，b＞0，求ab的最大值．

查看试题解析
18. 等比数列{a_n}中，已知a₁=2，a₄=16．

(1)、求数列{a_n}的通项公式a_n；

(2)、若a₃ ， a₅分别是等差数列{b_n}的第4项和第16项，求数列{b_n}的通项公式及前n项和S_n ．

查看试题解析
19. 已知△ABC的三个内角A，B，C所对应的边分别为a，b，c，且满足asinB= $\sqrt{3}$ bcosA．

(1)、求A的大小；

(2)、若a=7，b=5，求△ABC的面积．

查看试题解析
20. 如图，四边形ABCD是矩形，平面ABCD⊥平面BCE，BE⊥EC．

(1)、求证：平面AEC⊥平面ABE；

(2)、点F在BE上，若DE∥平面ACF，DC=CE= $\frac{1}{2}$ BC=3，求三棱锥A﹣BCF的体积．

查看试题解析
21. 已知点A（2，2），B（3，4），C（m，0），△ABC的面积为5．

(1)、求m的值；

(2)、若m＞0，∠BAC的平分线交线段BC于D，求点D的坐标．

查看试题解析
22. 已知数列{a_n}中，a₁=1，a₁+2a₂+3a₃+…+na_n= $\frac{n + 1}{2} a_{n + 1}$ （n≥1，n∈Z）

(1)、求数列{a_n}的通项公式a_n；

(2)、求数列{n²a_n}的前n项和T_n ．

查看试题解析