-
1、不等式组的最小整数解为 .
-
2、如图,是⊙的直径,点为⊙上一点,连接 , 过点作交⊙于点 , 连接、 , 若 , 则等于( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、斑马线的作用是为了引导行人安全地通过马路.某数学兴趣小组为了验证斑马线是由密若干条平行线组成的,在保证安全的前提下,按照如图方式分别测出 , 这种验证方法依据的基本事实是( )
 A、内错角相等,两直线平行 B、同位角相等,两直线平行 C、两直线平行,内错角相等 D、两直线平行,同位角相等
A、内错角相等,两直线平行 B、同位角相等,两直线平行 C、两直线平行,内错角相等 D、两直线平行,同位角相等 -
4、如图所示,一个圆柱体和长方体按如图所示的方式摆放,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
5、根据有理数加法法则,计算过程正确的是( )A、 B、 C、 D、
-
6、对凸四边形我们进行约定:
若四边形对角线既不垂直也不相等,叫做“线无垂等”四边形;
若四边形对角线垂直但不相等,叫做“线垂不等”四边形;
若四边形对角线相等但不垂直,叫做“线等不垂”四边形;
若四边形对角线既相等又垂直,叫做“线垂且等”四边形;
(1)、判断下列说法的正确性,正确的请在括号内打“√”;错误的打“×”①所有的平行四边形都是“线无垂等”四边形( )
②内角不是的菱形一定是“线垂不等”四边形( )
③邻边相等的矩形是“线垂且等”四边形( )
(2)、如图,在矩形中,P是边上一点,若;
①连接 , 四边形是“________”四边形;
②若 , 且 , 求的长.
(3)、二次函数的对称轴为直线 , 且与x轴交于A,B两点(A在B点左侧),且 , 点 , 都在函数图象上,若四边形是“线垂且等”四边形,求C点坐标. -
7、如图,在中,平分 , 交于点 , 交的延长线于点 .
 (1)、求证:;(2)、若 , , , 求的长和的面积.
(1)、求证:;(2)、若 , , , 求的长和的面积. -
8、2025年蛇年春晚吉祥物形象“巳升升”已正式发布亮相,因其憨态可掬的眉眼与满满的中式美好寓意,“巳升升”受到广大群众的喜爱.某厂家生产A,B两款“巳升升”吉祥物,已知A款吉祥物的批发单价比B款吉祥物的批发单价高20元.若花800元批发购买A款吉祥物的数量与花600元批发购买B款吉祥物的数量相同.(1)、求A,B两款“巳升升”吉祥物的批发单价分别是多少元?(2)、某网店从该厂家处批发购进了A,B两款型号的“巳升升”吉祥物共60个,A款吉祥物的数量不超过B款吉祥物数量的一半,B款吉祥物售价为80元/个,A款吉祥物的售价比B款吉祥物的售价高 . 若购进的这两种型号吉祥物全部售出,且要使得该网店所获利润最多,则该网店购进A款吉祥物多少个?最大利润是多少?
-
9、如图,在中, , , , 分别以点A,B为圆心,大于的长为半径画弧,两弧分别交于点M和N,作直线分别交于点D,E,连接
 (1)、求的长;(2)、求的周长.
(1)、求的长;(2)、求的周长. -
10、先化简,再求值: , 其中 .
-
11、一只皮箱的密码是一个三位数,小光说:“它是”;小明说:“它是”;小亮说:“它是”;已知每人都只猜对了位置不同的一个数字.这只皮箱的密码是 .
-
12、如图, , , , 两两不相交,且半径都是 , 则图中四个扇形(即阴影部分)的面积之和为 .

-
13、平面直角坐标系中的点在第二象限,则的取值范围在数轴上可表示为( )A、
 B、
B、 C、
C、 D、
D、
-
14、如图,内接于 , 连接 , 作交于点D,若 , 则的度数为( )
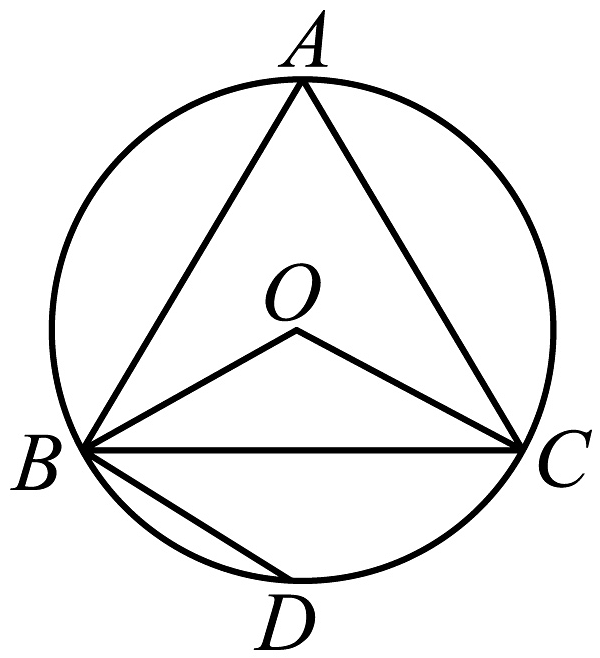 A、 B、 C、 D、
A、 B、 C、 D、 -
15、下列所给的事件中,是随机事件的是( )A、抛掷硬币时,正面朝上 B、任意画一个三角形,其内角和为 C、若 , 互为相反数,则 D、水中捞月
-
16、是人工智能研究实验室新推出的一种由人工智能技术驱动的自然语言处理工具,其技术底座有着多达175000000000个模型参数,数据175000000000用科学记数法表示为( )A、 B、 C、 D、
-
17、如图,是的直径, , 点E在的延长线上,且 .
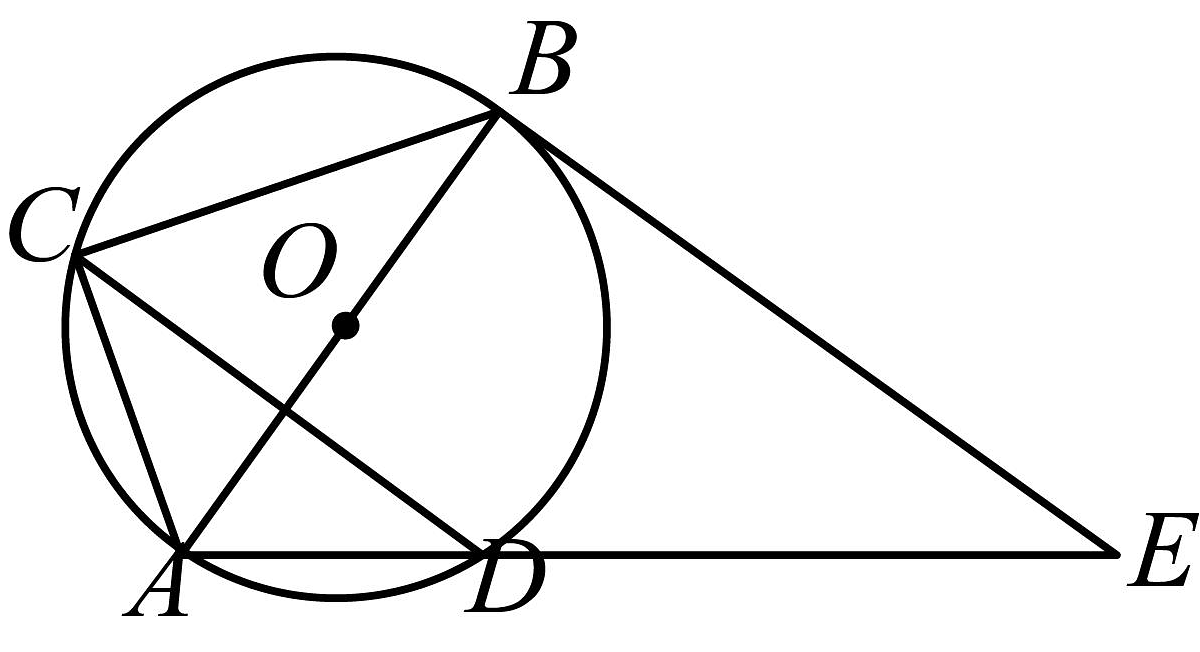 (1)、求证:是的切线;(2)、当的半径为2,时,求的值.
(1)、求证:是的切线;(2)、当的半径为2,时,求的值. -
18、如图,在平面直角坐标系中,将函数的图象向上平移3个单位长度,得到一次函数的图象,与反比例函数的图象交于点 . 过点作x轴的平行线分别交与的图象于C,D两点.
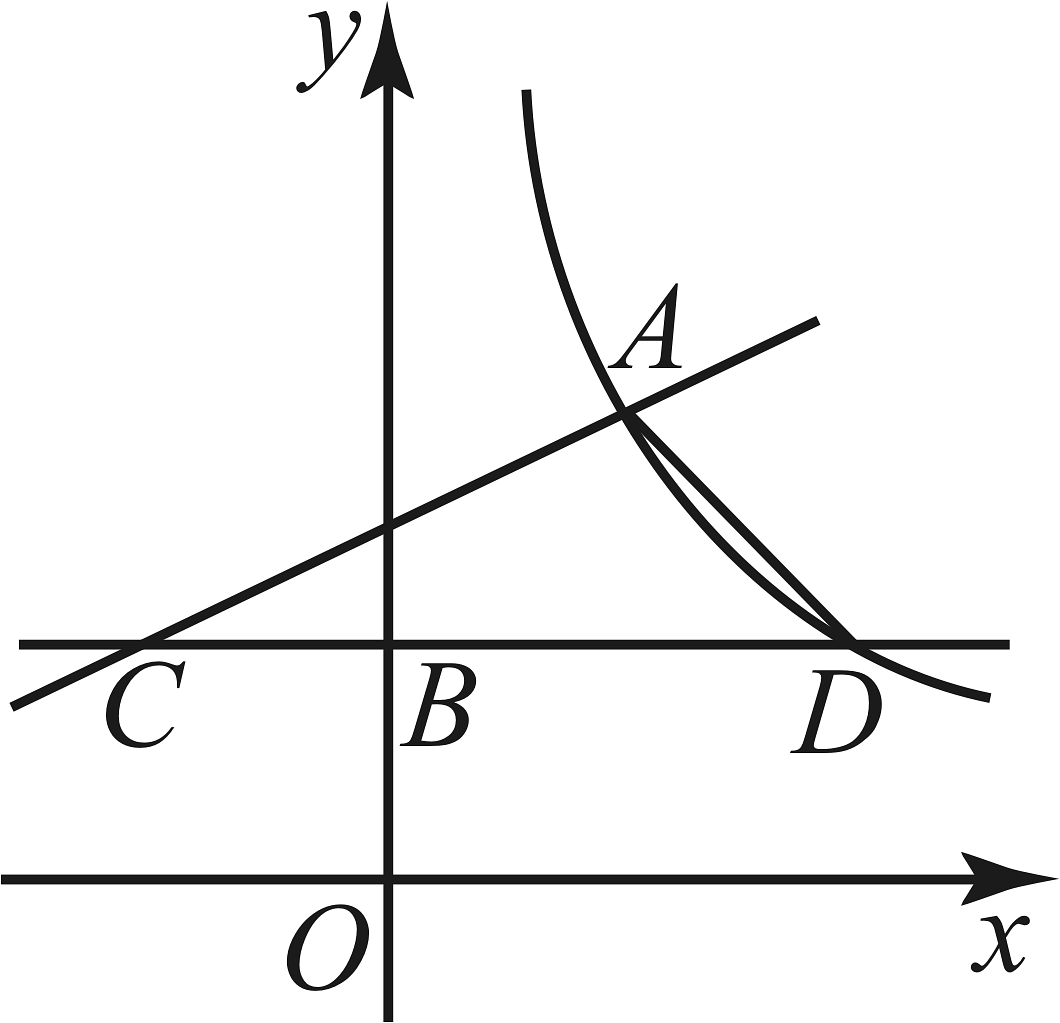 (1)、求一次函数和反比例函数的表达式;(2)、连接 , 求的面积.
(1)、求一次函数和反比例函数的表达式;(2)、连接 , 求的面积. -
19、习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和.甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒垂直于地面,测角仪 , 在两侧, , 点C与点E相距 (点C,H,E在同一条直线上),在D处测得简尖顶点A的仰角为 , 在F处测得筒尖顶点A的仰角为 . 求风电塔筒的高度.(参考数据: , , . )

-
20、马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、黑、白彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧.如图1的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图2,已知和圆上一点M.作法如下:
①以点M为圆心,长为半径,作弧交于A,B两点;
②延长交于点C;
即点A,B,C将的圆周三等分.
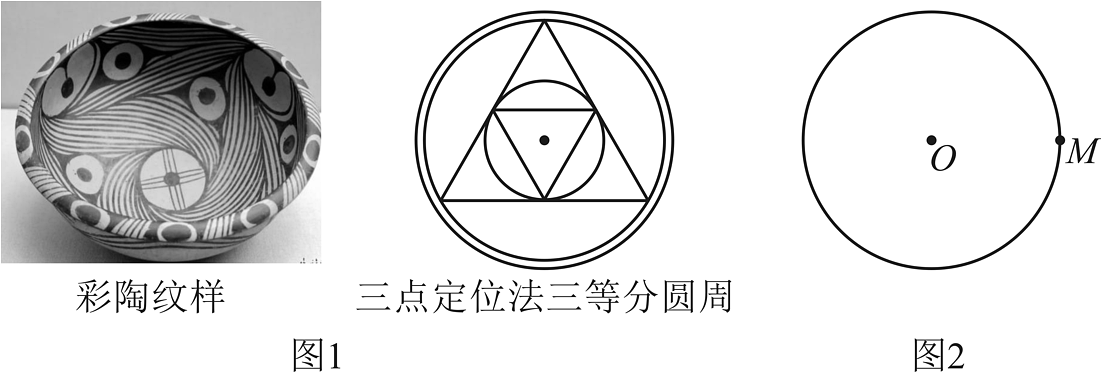 (1)、请你依据以上步骤,用不带刻度的直尺和圆规在图2中将的圆周三等分(保留作图痕迹,不写作法);(2)、根据(1)画出的图形,连接 , , , 若的半径为 , 则的周长为______ .
(1)、请你依据以上步骤,用不带刻度的直尺和圆规在图2中将的圆周三等分(保留作图痕迹,不写作法);(2)、根据(1)画出的图形,连接 , , , 若的半径为 , 则的周长为______ .