相关试卷

1、因式分解： $9 a^{2} - b^{2} =$ ．

查看解析
2、若二次函数的解析式为 $y = (x - 2 m) (x - 2) (1 \leq m \leq 5)$ ．若函数图象过点 $(p, q)$ 和点 $(p + 4, q)$ ，则q的取值范围是（　　）

A、 $- 12 \leq q \leq 4$ B、 $- 5 \leq q \leq 0$ C、 $- 5 \leq q \leq 4$ D、 $- 12 \leq q \leq 3$

查看解析
3、如图所示，在边长为12的正方形中ABCD中，有一个小正方形EFGH，其中点E、F、G分别在线段AB、BC、FD上，若 $B F = 3$ ，则小正方形的边长为（）

A、6 B、5 C、 $\frac{15}{4}$ D、 $2 \sqrt{3}$

查看解析
4、已知关于x的一元二次方程（m－1）x²－2x＋1＝0，要使该方程有实数根，则m必须满足（）

A、m＜2 B、m≤2 C、m＜2且m≠1 D、m≤2且m≠1

查看解析
5、某市城市轨道交通 $6$ 号线工程的中标价格是 $81750000$ 元， $81750000$ 精确到 $100000$ ，用科学记数法可表示为（）

A、 $8.17 \times 10^{7}$ B、 $8.17 \times 10^{8}$ C、 $8.18 \times 10^{7}$ D、 $8.18 \times 10^{8}$

查看解析
6、下列各数是正数的是（）

A、 $- \frac{1}{3}$ B、0 C、2 D、 $- 0.2$

查看解析
7、如图，在四边形 $A B C D$ 中， $A D ∥ C B$ ，点M在 $B C$ 上，点N在 $C D$ 上，且 $∠ A M N = ∠ A B C$ ， $\sin ∠ B A D = \frac{4}{5}$ ， $A B = B C = 5$ ， $A D = 16$ ．

(1)、求证： $∠ B A D = 2 ∠ A D C$ ．

(2)、如图①，当 $C M = C N$ 时，求 $B M$ 的长．

(3)、如图②，点E在线段 $A B$ 上，且 $B E = \frac{5}{3}$ ，过点E作 $E F ∥ A D$ ，交 $C D$ 于点F，在 $E F$ 的延 $A P$ 长线上有一点P，射线 $F D$ 上有一点Q，且 $∠ A P Q = ∠ A B C$ ．若 $E F = 3 P F$ ，求 $\frac{A P}{P Q}$ 的值．

查看解析
8、如图，已知抛物线 $y = x^{2} - b x + c$ 与x轴交于A， $B (1, 0)$ 两点，与y轴交于点 $C (0, - 2)$ ， E为x轴负半轴上的点，F为抛物线第一象限上的点， $∠ O E F = ∠ O A C$ ， D为直线 $E F$ 上的点．

(1)、求抛物线的解析式；

(2)、如图①，若四边形 $A C B D$ 是平行四边形，求直线 $E F$ 的解析式；

(3)、如图②，直线 $E F$ 满足（2）中的条件，M为直线 $E F$ 上的点，当点D在第一、象限中，且 $△ A D E ∽ △ D B M$ ，求点D的坐标．

查看解析
9、如图， $A B$ 为 $⊙ O$ 的直径，D，E为 $⊙ O$ 上的点， $\overset{⌢}{A E}$ = $\overset{⌢}{D E}$ ，延长 $B D$ 至点C，连接 $A C$ ， $∠ A B C = 2 ∠ C A F$ ，延长 $A E$ 与 $B C$ 交于点F， $A B = 10$ ， $\tan ∠ C A F = \frac{1}{2}$

(1)、求证： $A C$ 与 $⊙ O$ 相切．

(2)、求 $\sin ∠ A C F$ 的值．

查看解析
10、如图，B是反比例函数 $y = \frac{k}{x} (x > 0)$ 图象上的一点，点A的坐标为 $(2, 0), △ A O B$ 是等边三角形．

(1)、求该反比例函数的解析式；

(2)、若D为反比例函数图象上位于点B右边的一点，C为x轴上的点， $△ A C D$ 是等边三角形，求点D的坐标．

查看解析
11、随着汽车拥有量的持续增加，城市交通堵塞情况日益严重，为优化交管措施，相关部门对一城市主干道交通情况进行了调研．通常情况下，当主干道上的车流密度达到200辆 $/ km$ 时，造成堵塞，此时车流平均速度为 $0 km / h$ ；当车流密度不高于50辆 $/ km$ 时，车流平均速度为 $50 km / h$ ．研究表明：当 $50 \leq x \leq 200$ 时，车流平均速度v（单位： $km / h$ ）是车流密度x（单位：辆 $/ km$ ）的一次函数．

(1)、当 $50 \leq x \leq 200$ 时，求v关于x的函数解析式；

(2)、已知车流量 $=$ 车流密度 $\times$ 车流速度（车流量为单位时间内通过主干道上某观测点的车辆数，单位：辆 $/ h$ ），设车流量为y，请写出y关于车流密度x的函数解析式，并求出当车流密度x为多少时车流量y可以达到最大，求出最大值（精确到1辆 $/ h$ ）．

查看解析
12、“低碳生活，绿色出行”的理念逐渐深入人心，更多居民选择共享单车作为出行的交通工具，某中学课外兴趣小组为了解某小区居民每周使用共享单车时间的情况，随机抽取了该小区部分使用共享单车的居民进行调查（问卷调查表如图所示），并用调查结果绘制了图①、图②两幅统计图（均不完整），请根据统计图解答以下问题：

(1)、本次接受问卷调查的共有___________人；在扇形图中，“A”选项所占的百分比为___________．

(2)、扇形图中，“B”选项所对应的扇形圆心角的度数为___________．

(3)、请补全条形图．

(4)、若该小区共有1200名居民使用共享单车，请你估计这1200名居民使用共享单车的时间在“D”选项的有多少人．

查看解析
13、（1）计算： $\sqrt{27} - 3^{- 1} - {(\frac{1}{3} - π)}^{0} - 4 \sin 60 °$
（2）先化简，再求值： $(\frac{x^{2} + 1}{x} - 2) \div \frac{x^{2} - 1}{2 x}$ ，其中 $x = \sqrt{2}$ ．

查看解析
14、如图，在菱形 $A B C D$ 中， $∠ A B C = 60 °, A B = 6, A E = 4, B E$ 与 $A C$ 交于点O，F为 $A B$ ．上一点，且 $O F ∥ B C$ ，连接 $C F, C F$ 与 $B E$ 交于点M，则 $B M$ 的长为．

查看解析
15、已知不等式 $\frac{x - 2}{3} - 1 > - \frac{x}{2}$ 的解都能使得关于x的不等式 $(a - 3) x < 3 a - 1$ 成立，则a的取值范围是．

查看解析
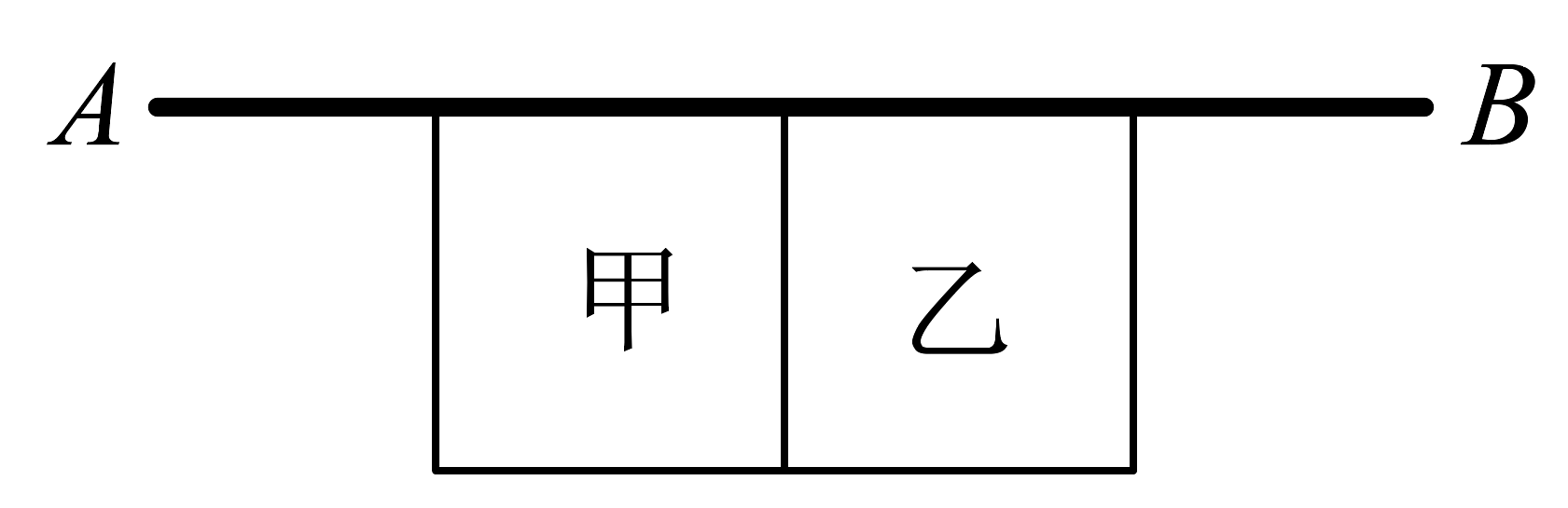
16、如图，某农场拟建造由甲．乙两个矩形组成的羊圈，饲养室的一面靠 $15 m$ 长的墙AB，其余的部分用栅栏围成甲、乙两部分．已知提前准备的建筑材料可以建造 $24 m$ 长的栅栏，则该羊圈最大面积可以建造 $m^{2}$

查看解析
17、一个不透明的袋中共有6个小球，分别为3个红球和3个黄球，它们除颜色外无其他差别．随机摸出两个小球，摸出两个颜色均为红色小球的概率为．

查看解析
18、如图，直线 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 交于一点，直线 $l_{1} ∥ l_{4}$ ，若 $∠ 1 = 118 °$ ， $∠ 2 = 86 °$ ，则 $∠ 3$ 的度数为．

查看解析
19、如图，在 $△ A O B$ 中， $∠ A O B = 90 °$ ， $tan ∠ A B C = \frac{1}{3}$ ， $⊙ O$ 与 $O B$ 交于点C， $A B$ 与 $⊙ O$ 相切，过点C作 $D C ⊥ O B$ ，交 $A B$ 于点D，M是边 $O A$ 上一动点，则当 $△ M C D$ 的周长最小时， $tan ∠ M C O$ 的值为（　　）

A、 $\frac{\sqrt{2}}{4}$ B、 $\frac{\sqrt{10} - 1}{6}$ C、 $\frac{\sqrt{10} - 2}{3}$ D、 $\frac{\sqrt{2}}{6}$

查看解析
20、二次函数 $y = a x^{2} + b x + c$ 图象的一部分如图所示，其对称轴是直线 $x = - 1$ ，且该图象过点 $A (- 3, 0)$ ．有下列说法：① $a b c < 0$ ；② $2 a - b + c < 0$ ；③ $4 a + 2 b + c < 0$ ；④若 $(- 3, y_{1}), (2, y_{2})$ 是抛物线上两点，则 $y_{1} < y_{2}$ ．其中正确的是（　　）

A、①② B、①②④ C、①②③ D、②④

查看解析

上一页 980 981 982 983 984 下一页跳转