相关试卷

1、下列4个箱子中，装有除颜色外完全相同的10个小球，任意摸出一个球，摸到红球可能性最小的是（）

A、 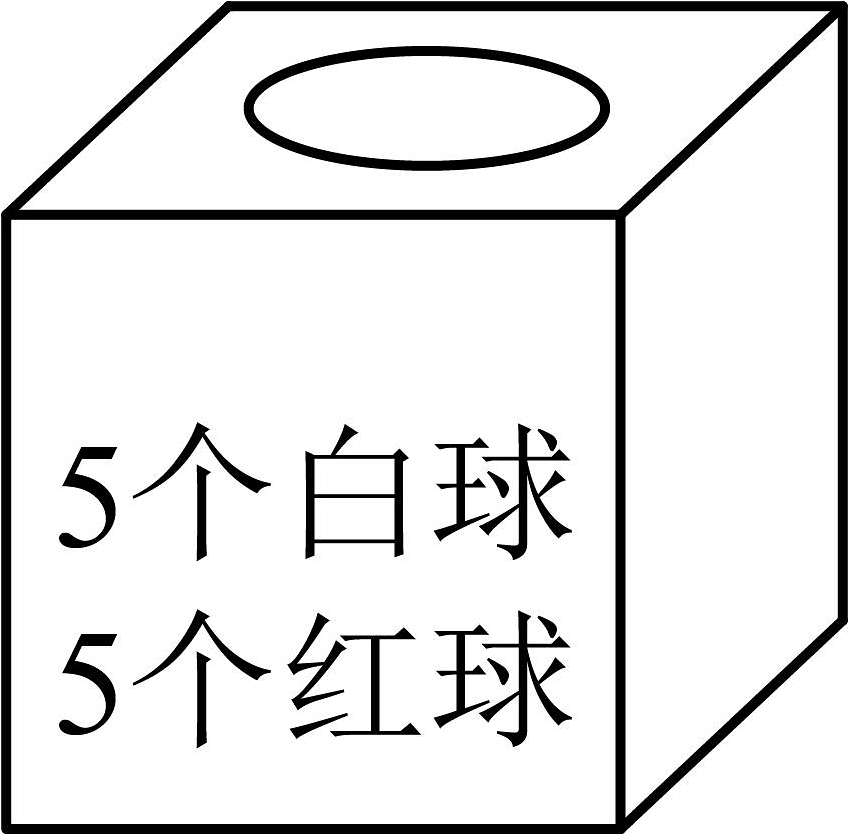B、 C、 D、

查看解析
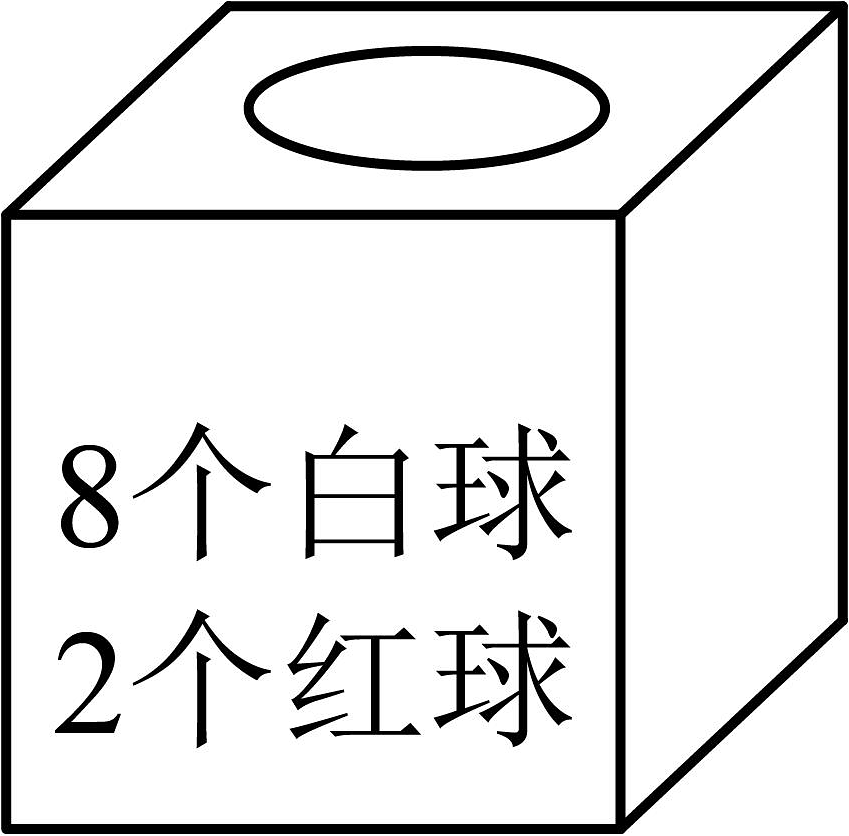
2、漫步城垣步道，寻迹贵阳“九门四阁”．如图是小李绘制的“九门四阁”平面示意图，若“大西门”所在位置的坐标是 $(- 3, 2)$ ， “老东门”所在位置的坐标是 $(3, 2)$ ，则“次南门”所在位置的坐标是（）

A、 $(- 3, 0)$ B、 $(- 2, 0)$ C、 $(- 1, 0)$ D、 $(0, 0)$

查看解析
3、化简 $\frac{2}{x + 1} + \frac{x - 1}{x + 1}$ 结果正确的是（）

A、 $\frac{3 - x}{x + 1}$ B、 $\frac{x - 1}{x + 1}$ C、 $1$ D、 $\frac{x}{x + 1}$

查看解析
4、如图，两直线 $a$ ， $b$ 被直线 $c$ 所截，已知 $a ∥ b$ ， $∠ 2 = 70 °$ ， $∠ 3 = 120 °$ ，则 $∠ 1$ 的度数为（）

A、 $50 °$ B、 $55 °$ C、 $60 °$ D、 $70 °$

查看解析
5、据统计，2024年中国芯片进口额近28000亿元人民币，分析进口芯片的结构，处理器及控制器占据了半壁江山，存储芯片占据了四分之一的份额，揭示了国内芯片市场的现状与挑战．数据28000用科学记数法表示为（）

A、 $28 \times 10^{3}$ B、 $2.8 \times 10^{3}$ C、 $2.8 \times 10^{4}$ D、 $0.28 \times 10^{5}$

查看解析
6、中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产名录，下面四幅作品分别代表二十四节气中的“立春”“谷雨”“芒种”“白露”，其中是轴对称图形的是（）

A、 B、 C、 D、

查看解析
7、如图甲所示，在正方形ABCD中，E是AD的中点.将△ABE沿BE折叠，使点A落在点F处，连结DF.

(1)、求证：∠BEF=∠DFE.

(2)、如图乙所示，延长DF交BC于点G，求 $\frac{D F}{D G}$ 的值.

(3)、如图丙所示，将 $△ C D G$ 沿DG折叠，此时点C的对应点H恰好落在BE上.若记 $△ B E F$ 和 $△ D G H$ 重叠部分的面积为 $S_{1}$ ，正方形ABCD的面积为 $S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的值.

查看解析
8、如图所示，抛物线 $y = - \frac{3}{4} x^{2} + \frac{9}{4} x + 3$ 交x轴的正半轴于点A，交y轴于点B，动点C（m，0）（0<m<4）在x轴上，过点C作x轴的垂线交线段AB于点D，交该抛物线于点P，连结OP交AB于点E.

(1)、求点A，B的坐标.

(2)、当m=2时，求线段PE的长.

(3)、当△BOE是以BE为腰的等腰三角形时，求m的值.（直接写出答案即可）

查看解析
9、如图甲所示，一吸管杯放置在水平桌面上，矩形ABCD为其横截面，OE为吸管，其示意图如图乙所示，AD=20cm，AB=6cm，OE=4cm，∠EOB=36°.

(1)、当杯子盖上时，吸管OE绕点O按顺时针方向转动到OB处，求OE扫过的面积.

(2)、当杯子绕点C按顺时针方向转动到OE与水平线CM平行时（如图丙所示）.
①求杯子与水平线CM的夹角∠BCM的度数.
②由图乙到图丙，点A的位置是升高了还是下降了?变化了多少厘米?（结果精确到0.1cm，参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）

查看解析
10、图甲是1个纸杯和6个叠放在一起的纸杯的示意图，量得1个纸杯的高为10cm，6个叠放在一起的纸杯的高为14cm.

(1)、求3个叠放在一起的纸杯的高为多少厘米.

(2)、若设x个叠放在一起的纸杯的高为ycm（如图乙所示），并将这x个叠放在一起的纸杯按如图丙所示的方式放进竖立的方盒中，方盒的厚度不计.
①求y关于x的函数表达式.
②若竖立的方盒的高为33.5cm，求x的最大值.

查看解析
11、某公司要招聘一名职员，根据实际需要，从学历、经验、能力和态度四个方面对甲、乙、丙三名应聘者进行测试，测试成绩如下表.
测试项目
应聘者
甲
乙
丙
学历
9
8
8
经验
8
6
9
能力
7
8
8
态度
5
7
5

(1)、若将学历、经验、能力和态度四项得分按1∶1∶1∶1的比例确定每人的最终得分，并以此为依据确定录用者，则谁将被录用?

(2)、如果这家公司较看重员工的学历和态度，且学历与态度的得分比例相同，经验与能力的得分比例相同，请你帮该公司设计一个四项得分的比例，并以此为依据确定录用者，则谁将被录用?

查看解析
12、数学课上老师要同学证明命题“对角线互相平分的四边形是平行四边形”是正确的.小红同学先任意画出△ABC，再取边AC的中点O，连结BO并延长到点D，使OD=OB，连结AD，CD（如图所示），并写出了如下尚不完整的已知和求证.

(1)、补全已知和求证（在方框中填空）.
已知：如图所示，在四边形ABCD中，
OD=OB，
OA=.
求证：四边形ABCD是四边形.

(2)、小红同学的思路是利用三角形全等，依据“一组对边平行且相等的四边形是平行四边形”来证明.请完成证明过程（可以用小红的思路，也可以用其他方法）.

查看解析

13、分解因式（3x+y）²-（x+3y）².小禾经过因式分解后，通过代入特殊值检验

小禾的解法：

（3x+y）²（x+3y）²

=（3x+y+x+3y）（3x+y-x+3y）

=（4x+4y）（2x+4y）

8（x+y）（x+2y）

小禾的检验：

当x=0，y=1时，

（3x+y）²-（x+3y）²

=1²-3²

=1-9

=-8

∵-8≠16

∴分解因式错误。

8（x+y）（x+2y）

=8×1×2

=16

任务：

(1)、小禾的解答是从第几步开始出错的?请指出他错误的原因.

(2)、请尝试写出正确的因式分解过程.

查看解析

14、

(1)、计算： $| - 2 | - 2 s i n 3 0^{°} + 202 3^{°}$ .

(2)、解不等式组： ${\begin{array}{l} 3 x - 1 > - 7, \\ 2 x < x + 2 . \end{array}$

查看解析
15、如图所示，等边△ABC内接于☉O，BC=6，D为 $\overset{⌢}{C A}$ 上一动点，过点B作射线DO的垂线，垂足为点E.

(1)、☉O的半径长为.

(2)、当点D由点C沿 $\overset{⌢}{C A}$ 运动到点A时，点E的运动路径长为.

查看解析
16、如图所示，在直角坐标系xOy中，矩形OACB被三条直线分割成六个小矩形，D是边OB的中点， $D E = 2 O E$ ，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过小矩形的顶点F，G，若图中的阴影矩形面积 $S_{1}$ 和 $S_{2}$ 满足 $2 S_{1} + S_{2} = 16$ ，则k的值为.

查看解析
17、分式方程 $\frac{3}{x + 1} = \frac{2}{x - 1}$ 的解为.

查看解析
18、在1，0，-2 $\sqrt{2}$ ， -3这四个数中，最小的是.

查看解析
19、已知二次函数 $y = - x^{2} + 2 c x + c$ 的图像经过点A（a，c），B（b，c），且满足 $0 < a + b < 2$ .当 $- 1 \leq x \leq 1$ 时，该函数的最大值m和最小值n之间满足的关系式为（）

A、 $n = m^{2} - 3 m$ B、 $m = n^{2} - 3 n$ C、 $n = m^{2} + m$ D、 $m = n^{2} + n$

查看解析
20、如图所示，正方形ABCD边长为4，点E在边AD上运动，在BE的左侧作等腰直角三角形BEF，∠BEF=90°，连结AF.喜欢探究的小亮通过独立思考，得到以下两个结论：①当点E与点D重合时，AF=4；②当线段AF最短时，AE=2.下列判断中，正确的是（）

A、①，②都正确 B、①，②都错误 C、①正确，②错误 D、①错误，②正确

查看解析

上一页 956 957 958 959 960 下一页跳转

测试项目	应聘者
测试项目	甲	乙	丙
学历	9	8	8
经验	8	6	9
能力	7	8	8
态度	5	7	5