相关试卷

1、图甲是1个纸杯和6个叠放在一起的纸杯的示意图，量得1个纸杯的高为10cm，6个叠放在一起的纸杯的高为14cm.

(1)、求3个叠放在一起的纸杯的高为多少厘米.

(2)、若设x个叠放在一起的纸杯的高为ycm（如图乙所示），并将这x个叠放在一起的纸杯按如图丙所示的方式放进竖立的方盒中，方盒的厚度不计.
①求y关于x的函数表达式.
②若竖立的方盒的高为33.5cm，求x的最大值.

查看解析
2、某公司要招聘一名职员，根据实际需要，从学历、经验、能力和态度四个方面对甲、乙、丙三名应聘者进行测试，测试成绩如下表.
测试项目
应聘者
甲
乙
丙
学历
9
8
8
经验
8
6
9
能力
7
8
8
态度
5
7
5

(1)、若将学历、经验、能力和态度四项得分按1∶1∶1∶1的比例确定每人的最终得分，并以此为依据确定录用者，则谁将被录用?

(2)、如果这家公司较看重员工的学历和态度，且学历与态度的得分比例相同，经验与能力的得分比例相同，请你帮该公司设计一个四项得分的比例，并以此为依据确定录用者，则谁将被录用?

查看解析
3、数学课上老师要同学证明命题“对角线互相平分的四边形是平行四边形”是正确的.小红同学先任意画出△ABC，再取边AC的中点O，连结BO并延长到点D，使OD=OB，连结AD，CD（如图所示），并写出了如下尚不完整的已知和求证.

(1)、补全已知和求证（在方框中填空）.
已知：如图所示，在四边形ABCD中，
OD=OB，
OA=.
求证：四边形ABCD是四边形.

(2)、小红同学的思路是利用三角形全等，依据“一组对边平行且相等的四边形是平行四边形”来证明.请完成证明过程（可以用小红的思路，也可以用其他方法）.

查看解析

4、分解因式（3x+y）²-（x+3y）².小禾经过因式分解后，通过代入特殊值检验

小禾的解法：

（3x+y）²（x+3y）²

=（3x+y+x+3y）（3x+y-x+3y）

=（4x+4y）（2x+4y）

8（x+y）（x+2y）

小禾的检验：

当x=0，y=1时，

（3x+y）²-（x+3y）²

=1²-3²

=1-9

=-8

∵-8≠16

∴分解因式错误。

8（x+y）（x+2y）

=8×1×2

=16

任务：

(1)、小禾的解答是从第几步开始出错的?请指出他错误的原因.

(2)、请尝试写出正确的因式分解过程.

查看解析

5、

(1)、计算： $| - 2 | - 2 s i n 3 0^{°} + 202 3^{°}$ .

(2)、解不等式组： ${\begin{array}{l} 3 x - 1 > - 7, \\ 2 x < x + 2 . \end{array}$

查看解析
6、如图所示，等边△ABC内接于☉O，BC=6，D为 $\overset{⌢}{C A}$ 上一动点，过点B作射线DO的垂线，垂足为点E.

(1)、☉O的半径长为.

(2)、当点D由点C沿 $\overset{⌢}{C A}$ 运动到点A时，点E的运动路径长为.

查看解析
7、如图所示，在直角坐标系xOy中，矩形OACB被三条直线分割成六个小矩形，D是边OB的中点， $D E = 2 O E$ ，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过小矩形的顶点F，G，若图中的阴影矩形面积 $S_{1}$ 和 $S_{2}$ 满足 $2 S_{1} + S_{2} = 16$ ，则k的值为.

查看解析
8、分式方程 $\frac{3}{x + 1} = \frac{2}{x - 1}$ 的解为.

查看解析
9、在1，0，-2 $\sqrt{2}$ ， -3这四个数中，最小的是.

查看解析
10、已知二次函数 $y = - x^{2} + 2 c x + c$ 的图像经过点A（a，c），B（b，c），且满足 $0 < a + b < 2$ .当 $- 1 \leq x \leq 1$ 时，该函数的最大值m和最小值n之间满足的关系式为（）

A、 $n = m^{2} - 3 m$ B、 $m = n^{2} - 3 n$ C、 $n = m^{2} + m$ D、 $m = n^{2} + n$

查看解析
11、如图所示，正方形ABCD边长为4，点E在边AD上运动，在BE的左侧作等腰直角三角形BEF，∠BEF=90°，连结AF.喜欢探究的小亮通过独立思考，得到以下两个结论：①当点E与点D重合时，AF=4；②当线段AF最短时，AE=2.下列判断中，正确的是（）

A、①，②都正确 B、①，②都错误 C、①正确，②错误 D、①错误，②正确

查看解析
12、在平面直角坐标系中，点P（2，4）是一个光源，木杆AB两端点的坐标分别是（1，2），（4，1），则木杆AB在x轴上的投影A'B'的长是（）

A、4 B、 $\frac{14}{3}$ C、 $\frac{9}{2}$ D、5

查看解析
13、如图所示，过直线AB外的点P作直线AB的平行线，下列作法中，错误的是（）

A、 B、 C、 D、

查看解析
14、某市为缓解交通拥堵，决定修建高架快速路.原计划用20个月完成这项工程，实际提前2个月完成该工程，求实际每月的工作效率比原计划提高的百分比?若设实际每月的工作效率比原计划提高的百分比是x%，根据题意可列的方程为（）

A、 $\frac{1}{18} = \frac{1}{20} (1 + x %)$ B、 $\frac{1}{20} = \frac{1}{18} (1 - x %)$ C、 $\frac{1}{18} = \frac{1}{20} (1 - x %)$ D、 $\frac{1}{20} = \frac{1}{18} (1 + x %)$

查看解析
15、对于一组统计数据：2，2，3，4，4.下列说法中，错误的是（）

A、平均数是3 B、方差是0.8 C、中位数是3 D、众数是4

查看解析
16、如图所示，在菱形ABCD中，∠C=80°，则∠ABD的度数为（）

A、80° B、70° C、60° D、50°

查看解析
17、如图所示，该简单几何体的俯视图是（）

A、 B、 C、 D、

查看解析
18、小王在学习浙教版《义务教育教科书数学九年级上册》第72页例2后，进一步开展探究活动：将一个矩形ABCD绕点A按顺时针方向旋转α（0°<α≤90°），得到矩形AB'C'D'，连结BD.

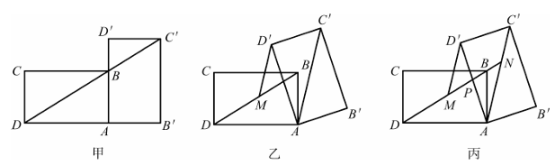(1)、如图甲所示，当α=90°时，点C'恰好在DB延长线上.若AB=1，求BC的长.

(2)、如图乙所示，连结AC'，过点D'作D'M∥AC'交BD于点M.线段D'M与DM相等吗?请说明理由.

(3)、在（2）的条件下，射线DB分别交AD'，AC'于点P，N（如图丙所示），发现线段DN，MN，PN存在等式数量关系，请写出这个等式，并加以证明.

查看解析
19、【问题】
如图所示，在▱ABCD中，AB=8，AD=5，∠DAB，∠ABC的平分线AE，BF，求EF的长.

(1)、把【问题】中的条件“AB=8”去掉，其余条件不变.
①当点E与点F重合时，求AB的长.
②当点E与点C重合时，求EF的长.

(2)、把【问题】中的条件“AB=8，AD=5”去掉，其余条件不变，C，D，E，F相邻两点间的距离相等时，求 $\frac{A D}{A B}$ 的值.

查看解析
20、在正方形ABCD中，AB=8，E，F分别是BC，AB边上的动点，以DF、EF为边作平行四边形EFDG.

(1)、如图甲，连结AE，交DF于点O，若AF=BE，
①试说明EG与AE的关系；
②求线段DG的最小值；

(2)、如图乙，若四边形EFDG为菱形，请判断线段BE与AF之间的数量关系，并说明理由.

查看解析

上一页 953 954 955 956 957 下一页跳转

测试项目	应聘者
测试项目	甲	乙	丙
学历	9	8	8
经验	8	6	9
能力	7	8	8
态度	5	7	5