-
1、在平面直角坐标系xOy中,点 P 的坐标为(m+1,m-1).
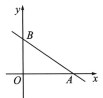 (1)、试判断点 P 是否在一次函数y=x-2的图象上,并说明理由.(2)、如图,一次函数 的图象与x轴、y轴分别相交于点A,B,若点 P 在△AOB 的内部,求 m 的取值范围.
(1)、试判断点 P 是否在一次函数y=x-2的图象上,并说明理由.(2)、如图,一次函数 的图象与x轴、y轴分别相交于点A,B,若点 P 在△AOB 的内部,求 m 的取值范围. -
2、已知点P(a,b)在直线y=-3x-4上,且2a-5b≤0,则下列不等式一定成立的是( ).A、 B、 C、 D、
-
3、坐标平面上点 P(a,b)先绕点(1,5)逆时针方向旋转90°,再关于直线y=-x 对称,经两次变换后得到点P'(-6,3).则b-a 的值为( ).A、1 B、3 C、5 D、7 E、9
-
4、当自变量-1≤x≤3时,函数y=|x-k|(k为常数)的最小值为k+3,则满足条件的k的值为.
-
5、设直线 (n为自然数)与两坐标轴围成的三角形面积为 Sn(n=1,2,…,2005),则 的值为.
-
6、如图,在平面直角坐标系中,直线y=-x+3过点A(5,m),且与y轴交于点B,把点A 向左平移2个单位长度,再向上平移4个单位长度,得到点C.过点C且与直线y=2x平行的直线交y轴于点D.
 (1)、求直线CD 的解析式.(2)、直线AB与CD 交于点 E,将直线CD 沿 EB 方向平移至经过点 B 的位置结束,求直线CD 在平移过程中与x轴交点的横坐标的取值范围.
(1)、求直线CD 的解析式.(2)、直线AB与CD 交于点 E,将直线CD 沿 EB 方向平移至经过点 B 的位置结束,求直线CD 在平移过程中与x轴交点的横坐标的取值范围. -
7、若 abc<0,直线 不经过第四象限,则直线y=(a+b)x+c一定不经过( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
8、在平面直角坐标系中,过点(-2,3)的直线l经过一、二、三象限,若点(0,a),(-1,b),(c,-1)都在直线l上,则下列判断正确的是( ).A、a<b B、a<3 C、b<3 D、c<-2
-
9、设有一次函数y=kx+b(k,b为常数),下表中给出5组自变量和相应的函数值,其中只有一组的函数值计算有误,则这个函数值是.
x
1
2
3
4
5
y
4
7
10
14
16
-
10、(1)、已知直线y=2x+(3-a)与x轴的交点在A(2,0),B(3,0)之间(包括A,B 两点),则a的取值范围是.(2)、在平面直角坐标系中,已知点A(2,3),B(4,7),直线y= kx-k(k≠0)与线段AB 有交点,则k 的取值范围为.
-
11、如图,在平面直角坐标系中,直线 分别交x轴、y 轴于点 A,B,将△AOB 绕点 O 顺时针旋转 90°后得到△A'OB'.
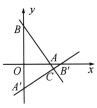 (1)、求直线A'B'的解析式.(2)、若直线A'B'与直线l 相交于点C,求△A'CB 的面积.
(1)、求直线A'B'的解析式.(2)、若直线A'B'与直线l 相交于点C,求△A'CB 的面积. -
12、对于平面直角坐标系中的任意两点P1(x1 , y1),P2(x2 , y2),我们把 叫作 P1 , P2两点间的直角距离,记作d(P2 , P2).(1)、已知O为坐标原点,动点 P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在直角坐标系中画出所有符合条件的点 P所组成的图形.(2)、设P0(x0 , y0)是一定点,Q(x,y)是直线 y= ax+b上的动点,我们把d(P0 , Q)的最小值叫作 P0到直线 y=ax+b 的直角距离.试求点 M(2,1)到直线y=x+2的直角距离.
-
13、(1)、已知函数y=kx+b的图象如右图,则y=2kx+b的图象可能是( ).
 A、
A、 B、
B、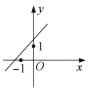 C、
C、 D、
D、 (2)、如图,平面直角坐标系xOy中,点A 的坐标为(9,6),AB⊥y 轴,垂足为 B,点 P 从原点O出发向x轴正方向运动,同时,点Q 从点A 出发向点 B 运动,当点 Q 到达点 B 时,点P,Q同时停止运动,若点 P 与点Q 的速度之比为1:2,则下列说法正确的是( ).
(2)、如图,平面直角坐标系xOy中,点A 的坐标为(9,6),AB⊥y 轴,垂足为 B,点 P 从原点O出发向x轴正方向运动,同时,点Q 从点A 出发向点 B 运动,当点 Q 到达点 B 时,点P,Q同时停止运动,若点 P 与点Q 的速度之比为1:2,则下列说法正确的是( ). A、线段 PQ 始终经过点(2,3) B、线段 PQ 始终经过点(3,2) C、线段 PQ 始终经过点(2,2) D、线段 PQ 不可能始终经过某一定点
A、线段 PQ 始终经过点(2,3) B、线段 PQ 始终经过点(3,2) C、线段 PQ 始终经过点(2,2) D、线段 PQ 不可能始终经过某一定点 -
14、
 (1)、如图①,在平面直角坐标系中,M是直线y=-x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点 M 的横坐标为m,则m 的取值范围为.(2)、如图②,有一种动画程序,屏幕上正方形区域ABCD 表示黑色物体甲,其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到区域甲时,甲由黑变白,则b的取值范围为时,甲能由黑变白.
(1)、如图①,在平面直角坐标系中,M是直线y=-x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点 M 的横坐标为m,则m 的取值范围为.(2)、如图②,有一种动画程序,屏幕上正方形区域ABCD 表示黑色物体甲,其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到区域甲时,甲由黑变白,则b的取值范围为时,甲能由黑变白. -
15、我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用现代式子表示即为: ①(其中a,b,c为三角形的三边长,S为面积).而文明古国古希腊也有求三角形面积的“海伦公式”: ②(其中(1)、若已知三角形的三边长分别为5,7,8,试分别运用公式①和公式②,计算该三角形的面积S.(2)、你能否由公式①推导出公式②?请试试.
-
16、求比大的最小整数.
-
17、计算的值等于( ).A、 B、 C、 D、
-
18、 a,b为有理数,且满足等式 , 则a+b 的值为( ).A、2 B、4 C、6 D、8
-
19、已知 则 .
-
20、当 , 化简 的结果是.