-
1、如图，AD 是 的角的角平分线， 垂足为E， 交ED 的延长线于点F，若BC恰好平分. ， .给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF.其中正确的结论共有( ).
A、4个 B、3个 C、2个 D、1个 -
2、如图，在△ABC 中，AD⊥BC于D，CE⊥AB于E，AD，CE交于点H，已知EH=EB=3，AE=4，则CH 的长是( ).
A、1 B、2 C、3 D、4 -
3、一个三角形的三条边的长分别为3，5，7，另一个三角形的三条边的长分别为3，3x-2，2x-1.若这两个三角形全等，则x 的值是.
-
4、如图， AC平分∠DCB，CB=CD，DA 的延长线交BC 于点E，若∠EAC=49°，则∠BAE 的度数为.
-
5、如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E，AD=3，BE=1，则DE的长为.
-
6、 问题提出 学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
初步思考 我们不妨将问题用符号语言表示为：在△ABC 和△DEF中，AC=DF，BC=EF，∠B=∠E.然后，对∠B 进行分类，可分为“∠B 是直角、钝角、锐角”三种情况进行探究.
深入探究
(1)、第一种情况：当∠B 是直角时，△ABC≌△DEF.如图①，在△ABC 和△DEF 中，AC=DF，BC=EF，∠B=∠E=90°，根据 ， 可以知道Rt△ABC≌Rt△DEF.
(2)、第二种情况：当∠B 是钝角时，△ABC≌△DEF.如图②，在△ABC 和△DEF 中，AC=DF，BC=EF，∠B=∠E，且∠B，∠E 都是钝角.求证：△ABC≌△DEF.
(3)、第三种情况：当∠B 是锐角时，△ABC 和△DEF 不一定全等.在△ABC 和△DEF 中，AC= DF，BC =EF，∠B=∠E，且∠B，∠E 都是锐角，请你用尺规在图③中作出△DEF，使△DEF 和△ABC 不全等.(不写作法，保留作图痕迹)
(4)、∠B 还要满足什么条件，就可以使△ABC≌△DEF?请直接填写结论：在△ABC 和△DEF 中，AC=DF，BC=EF，∠B=∠E，且∠B，∠E 都是锐角，若 ， 则△ABC≌△DEF.
-
7、 如图，已知△ABC 中，∠A=60°，BE，CD 分别平分∠ABC，∠ACB，P 为BE，CD 的交点.求证：BD+CE=BC.
-
8、如图，在△ABC中，D是BC边上的一点，E 是 AD 上的一点，且AD=DC，∠DEC=∠ABC，求证：AB=CE.
-
9、如图，在平面直角坐标系中，已知点A(3，0)，B(0，5)，点 C 在第一象限，以 BC 为边作等腰直角三角形ABC，求点 C 的坐标.
-
10、 如图，在四边形ABCD 中，对角线AC 平分∠BAD，AB>AD，下列结论正确的是( ).
A、AB-AD>CB-CD B、AB-AD=CB-CD C、AB-AD<CB-CD D、AB-AD 与CB-CD 的大小关系不确定 -
11、如图，△ABC 与△AEF 中，AB=AE，BC=EF.∠B=∠E，AB交EF于D.给出下列结论：①∠AFC=∠C；②DF=CF；③BC=DE+DF；④∠BFD=∠CAF.其中正确的结论是(填写所有正确结论的序号).
-
12、在平面直角坐标系xOy中，对于A，A'两点，若在 y 轴上存在点T，使得 且TA=TA'，则称A，A'两点互相关联，把其中一个点叫作另一个点的关联点.已知点 M(-2，0)，N(-1，0)，点Q(m，n)在一次函数y=-2x+1的图象上.
(1)、①如图，在点 B(2，0)，C(0，-1)，D(-2，-2)中，点 M 的关联点是(填“B”“C”或“D”).②若在线段 MN 上存在点 P(1，1)的关联点 P'，则点 P'的坐标是.
(2)、若在线段 MN 上存在点Q 的关联点Q'，求实数m 的取值范围.(3)、分别以点E(4，2)，Q为圆心，1为半径作⊙E，⊙Q.若对⊙E 上的任意一点G，在⊙Q上总存在点G'，使得G，G'两点互相关联，请直接写出点 Q 的坐标. -
13、在平面直角坐标系中，已知O为坐标原点，点A(3，0)，B(0，4).以点 A 为旋转中心，把△ABO顺时针旋转，得△ACD，记旋转角为α，∠ABO 为β.
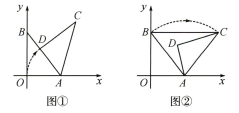(1)、如图①，当旋转后点 D 恰好落在AB 边上时，求点 D 的坐标.(2)、如图②，当旋转后满足 BC∥x轴时，求α与β之间的数量关系.(3)、当旋转后满足∠AOD=β时，求直线CD 的解析式. -
14、如图①，在△ABC中，AB=BC，BD⊥AC于点D(AD>BD).动点M从A 点出发，沿折线AB→BC方向运动，运动到点C停止.设点M 的运动路程为x，△AMD 的面积为y，y与x的函数图象如图②，则AC 的长为( ).
A、3 B、6 C、8 D、9 -
15、如图，在直角坐标系中，矩形 ABCO 的边OA 在x 轴上，边OC 在y 轴上，点 B 的坐标为(1，3)，将矩形沿对角线AC 翻折，B 点落在D 点的位置，且AD 交y轴于点E.那么点 D 的坐标为( ).
A、 B、 C、 D、 -
16、如图，点A、点B 的坐标分别为(-1，1)，(3，2)，P为x轴上一点，且P 到A，B的距离之和最小，则点 P 的坐标为.
-
17、如图，在平面直角坐标系xOy 中，直线y=-x+m分别交x轴、y轴于点A，B，已知点C(2，0)，设点 P 为线段OB 的中点，连接 PA，PC，若∠CPA=∠ABO，则m 的值为.
-
18、如图，已知A(6，0)，B(8，5)，将线段OA 平移至CB，点 D 在x 轴正半轴上(不与点A 重合)，连接OC，AB，CD，BD.
(1)、求对角线AC 的长.(2)、设点 D 的坐标为(x，0)，△ODC 与△ABD 的面积分别记为S1 ， S2.设、 写出S 关于x 的函数解析式，并探究是否存在点 D 使S 与△DBC 的面积相等，如果存在，用坐标形式写出点 D 的位置，如果不存在，说明理由. -
19、如图①，点 F 从菱形ABCD 的顶点A 出发，沿A→D→B 以1cm/s的速度匀速运动到点 B.图②是点 F 运动时，△FBC 的面积y(cm2)随时间x(s)变化的图象，则a 的值为( ).
A、 B、2 C、 D、 -
20、如图，已知A 点坐标为(5，0)，直线y=x+b(b≥0)与y轴交于点B，连接AB，∠α=75°，则b的值为( ).
A、3 B、 C、4 D、