相关试卷

1、如图，将边长为 $5 c m$ 的等边 $△ A B C$ 沿边 $B C$ 向右平移 $4 c m$ 得到 $△ A^{'} B^{'} C^{'}$ ，则四边形 $A B C^{'} A^{'}$ 的周长为（）

A、 $28 c m$ B、 $25 c m$ C、 $23 c m$ D、 $21 c m$

查看解析
2、如果n边形的内角和是它外角和的2倍，则 $n$ 等于（）

A、 $4$ B、 $5$ C、 $6$ D、 $7$

查看解析
3、下列命题为假命题的是（）

A、两点确定一条直线 B、若 $|a| > |b|$ ，则 $a > b$ C、等角的余角相等 D、两直线平行，同位角相等

查看解析
4、若分式 $\frac{x + 2}{x - 2}$ 的值为零，则x等于（　　）

A、0 B、2 C、 $- 2$ D、 $\pm 2$

查看解析
5、分解因式：

(1)、 $6 x^{2} y^{3} + 15 x y^{2} z$ ；

(2)、 $m (n - 1) + (1 - n)$ ．

查看解析
6、如图1，已知四边形 $A B C D$ 中， $A B = B C = C D = 4 ， ∠ B = ∠ B C D = α (60 ° < α \leq 90 °)$

(1)、点 $E$ 、 $F$ 分别是 $A B$ 、 $B C$ 边上动点，且 $B E = C F$ ，连接 $C E$ 与 $D F$ ，交于点 $G$ ，求 $∠ D G E$ 的度数（用 $a$ 表示）；

(2)、当 $α = 90 °$ 时，
①点 $F$ 是 $B C$ 边上动点，将 $△ C D F$ 沿着 $D F$ 翻折，若点 $C$ 的对应点刚好落在对角线 $B D$ 上，求此时 $C F$ 的长度；
②如图2， $N$ 在 $C D$ 上运动， $F$ 在射线 $B C$ 上运动， $B N$ 与 $A F$ 交于点 $M$ ，且满足 $∠ N B C = \frac{1}{2} ∠ B A F$ ， $P$ 是 $B M$ 中点，求 $\frac{\sqrt{5}}{5} D P + C P$ 的最小值．

查看解析
7、已知二次函数 $y = a x^{2} + b x + c$ 图象的对称轴为直线 $x = 1$ ，且与 $x$ 轴的一个交点为 $A (3 ， 0)$ ，与 $y$ 轴交点为 $B (0 ， 3)$ ．

(1)、求二次函数的解析式；

(2)、点 $P$ 为 $∠ O A B$ 内部一个动点，且 $A P = 3$ ，点 $P$ 关于直线 $A B$ 的对称点为 $P_{1}$ ，点 $P$ 关于 $x$ 轴的对称点为 $P_{2}$ ，问 $P_{1} P_{2}$ 的距离是定值吗？若为定值，请求出距离：若不是定值，请说明理由；

(3)、点 $C$ 为二次函数 $y = a x^{2} + b x + c$ 与 $x$ 轴的另一个交点，点 $Q$ 为二次函数 $y = a x^{2} + b x + c$ 上一点，若 $∠ Q A B = ∠ O B A - ∠ O B C$ ，求点 $Q$ 的坐标．

查看解析
8、数学兴趣小组了解到一款如图1所示的电子托盘秤，它是通过所称重物调节可变电阻 $R$ 的大小，从而改变电路中的电流 $I$ ，最终通过显示器显示物体质量．已知可变电阻 $R$ （单位： $k Ω$ ）与物体质量 $m$ （单位： $kg$ ）之间的关系如图2所示，电流 $I$ （单位： $mA$ ）与可变电阻 $R$ 之间关系为 $I = \frac{6}{R + 3} (R \geq 0)$ ．

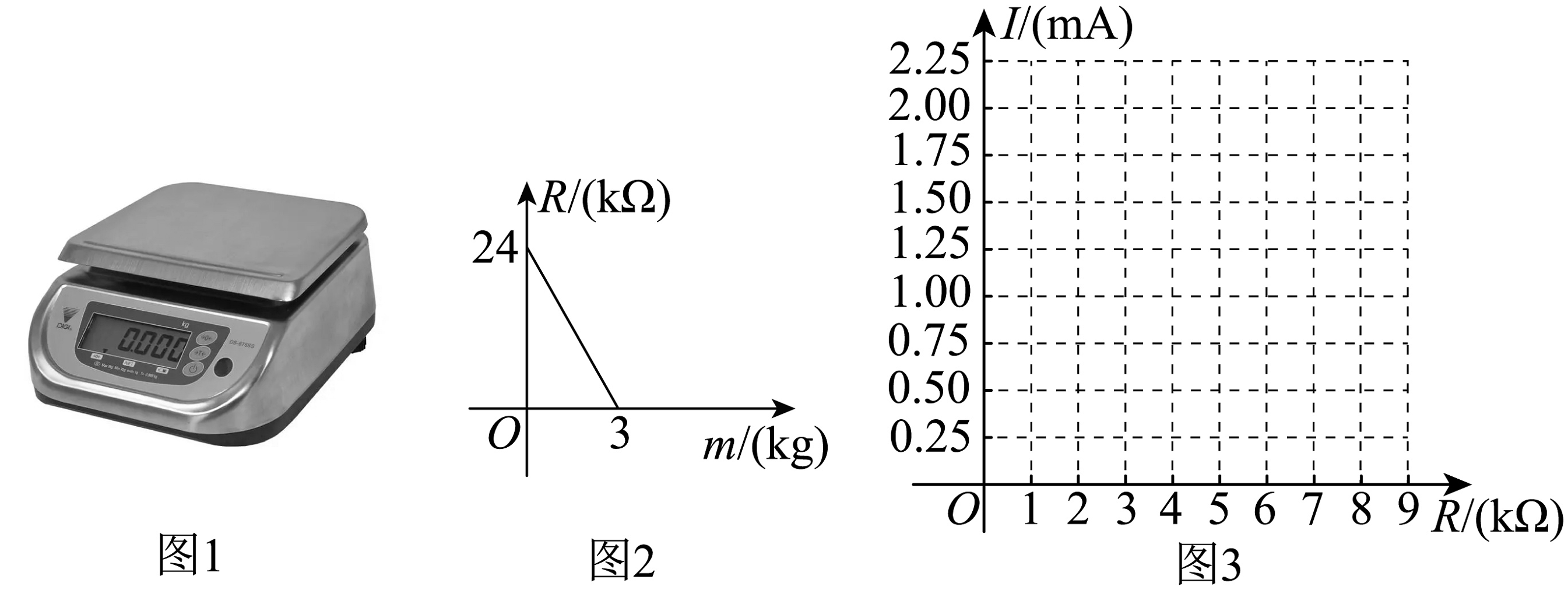(1)、小组先探究函数 $I = \frac{6}{R + 3} (R \geq 0)$ 的图象与性质，并根据 $I$ 与 $R$ 之间关系得到如下表格：
$R (kΩ)$
0
1
2
3
4
5
6
7
．．．
$I (mA)$
2
1.5
1.2
$p$
$\frac{6}{7}$
0.75
$\frac{2}{3}$
0.6
．．．
①表格中的 $p =$ ___________；
②请在图3中画出 $I = \frac{6}{R + 3} (R \geq 0)$ 对应的函数图象；

(2)、该小组综合图2和图3发现， $I$ 随着 $m$ 的增大而___________；（填“增大”或“减小”）

(3)、若将该款电子秤中的电路电流范围设定为 $0.2 < I < 0.4$ （单位： $mA$ ），判断该电子托盘秤能否称出质量为 $2 kg$ 的物体的质量？请说明理由．

查看解析
9、在《黑神话·悟空》中，“天命人”需要跨越一座被妖雾笼罩的山峰，由于雾气被施法，无法飞行，只能缓缓爬山，路线示意图如图②，“天命人”从山脚 $A$ 出发，沿 $A B$ 走400米到 $B$ 点，再沿 $B C$ 到山顶 $C$ 点，已知山高 $C F$ 为384米， $B E ∥ A F$ ， $B D ⊥ A F$ ， $C E ⊥ B E$ 交 $A D$ 的延长线于点 $F$ ， $∠ 1 = 30 °$ ， $∠ 2 = 50 °$ ．（图中所有点均在同一平面内）

(1)、求 $B D$ 的长；

(2)、求“天命人”从山脚 $A$ 点到达山顶 $C$ 点共走了多少米？（结果精确到0.1米）．（参考数据： $sin 50 ° \approx 0.77$ ， $cos 50 ° \approx 0.64$ ， $tan 50 ° \approx 1.19$ ）

查看解析
10、广府文化传承小组为了解中学生对传统艺术的了解情况，随机抽取某校一批学生进行调查，要求他们从粤剧、醒狮、广绣和广彩四种艺术中选择“最感兴趣的一项”．调查结果部分数据如下：
项目
频数
频率
粤剧
30
$b$
醒獅
45
$0.375$
广绣
$a$
$0.25$
广彩
15
$0.125$

(1)、由上表可得， $a =$ ___________， $b =$ ___________，总调查人数为___________人．

(2)、该校有两名艺术老师打算开设两个不同的特色课程，课程内容从以上四种广府文化项目中任选两个，请求出两个老师开设的特色课程中有粤剧课程的概率．

查看解析
11、如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C < B C$ ， $D$ 为 $B C$ 上一点，且 $D$ 到 $A$ ， $B$ 两点的距离相等．

(1)、用直尺和圆规作出点 $D$ 的位置；（不写作法，保留作图痕迹）

(2)、连结 $A D$ ，若 $A C = 3$ ， $B C = 9$ ，求 $C D$ 的长．

查看解析
12、先化简，再求值： $\frac{a + 1}{a - 2} \cdot \frac{a^{2} - 4}{a^{2} + 2 a + 1} \div \frac{1}{a^{2} - 1}$ 其中 $a^{2} + a = 1$ ．

查看解析
13、求满足不等式组 $\{\begin{array}{l} 3 x \leq x + 6 ① \\ x + 3 > 1 ② \end{array}$ 的所有整数解的和．

查看解析
14、如图，在正方形 $A B C D$ 中， $A B = 2 ， E$ 是平面内一点， $∠ A E D = 45 °$ ，连接 $D E$ ．过点 $A$ 作 $A E$ 的垂线交直线 $D E$ 于点 $P$ ．下列结论：① $△ A P D ≌ △ A E B$ ；② $E B ⊥ E D$ ；③当 $∠ A D E = 30 °$ 时， $A E = \sqrt{3}$ ；④ $C P$ 的最小值为 $\sqrt{10} - \sqrt{2}$ ．其中正确的结论是．

查看解析
15、在实数范围内定义运算“☆”和“★”，其规则为： $a ☆ b = a^{2} - b^{2}$ ， $a ★ b = \frac{a b}{2}$ ，则方程 $2 ☆ x = x ★ 6$ 的解为．

查看解析
16、若 $x^{2} + 3 x$ 的值为5，则 $- 3 x^{2} - 9 x + 20$ 的值为

查看解析
17、如图，在平行四边形 $A B C D$ 中， $∠ A B C$ 的角平分线交边 $A D$ 于点 $E$ ， $∠ A E B = 25 °$ ，则 $∠ D$ 的度数是．

查看解析
18、 $2025^{2} - 2024^{2} =$ ．

查看解析
19、如图，在矩形 $A B C D$ 中， $A B = 4$ ， $B C = 4 \sqrt{3}$ ，连接 $A C$ ，以点C为圆心， $C D$ 为半径作弧交 $B C$ 于点E，连接 $A E$ ．则图中阴影部分的面积为（）

A、 $8 + \frac{4 π}{3}$ B、 $2 + \frac{4 π}{2}$ C、 $4 + \frac{4 π}{3}$ D、 $8 + \frac{2 π}{3}$

查看解析
20、如图，在等腰三角形 $A B C$ 中， $∠ A B C = 90 °$ ， $D$ 为 $A C$ 边上中点，过 $D$ 点作 $D E ⊥ D F$ 交 $A B$ 于 $E$ ，交 $B C$ 于 $F$ ，若 $A B$ 的长为8，则四边形 $B F D E$ 的面积为（　　）

A、14 B、16 C、18 D、20

查看解析

上一页 770 771 772 773 774 下一页跳转

$R (kΩ)$	0	1	2	3	4	5	6	7	．．．
$I (mA)$	2	1.5	1.2	$p$	$\frac{6}{7}$	0.75	$\frac{2}{3}$	0.6	．．．

项目	频数	频率
粤剧	30	$b$
醒獅	45	$0.375$
广绣	$a$	$0.25$
广彩	15	$0.125$