相关试卷

1、如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， $C D$ 是 $A B$ 边上的高， $A B = 4$ ，若圆 $D$ 是以点 $D$ 为圆心， $1.4$ 为半径的圆，那么圆 $D$ 与直线 $A C$ 的关系是（　　）

A、相切 B、相离 C、相交 D、不能确定

查看解析
2、双曲线与直线交于A、B两点，要使反比例函数的值小于一次函数的值，则x的取值范围是（　　）

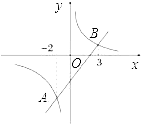A、x＞3 B、x＜﹣2 C、﹣2＜x＜0或x＞3 D、x＜﹣2或0＜x＜3

查看解析
3、某校随机抽取50名学生进行每周课外阅读时间的问卷调查，将调查结果制成频数直方图如图所示（每组包含最大值，不包含最小值）．估计该校2000名学生中每周阅读时间多于6小时的学生共有（）

A、20人 B、396人 C、800人 D、1080人

查看解析
4、下列AI软件的图标中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看解析
5、下面各数中最小的是（　　）

A、 $- 7$ B、0 C、 $\sqrt{5}$ D、 $- \frac{1}{2}$

查看解析
6、【思考探究】
（1）数学活动课上，老师出示了一个问题：如图1，在矩形 $A B C D$ 中， $E$ 是边 $A B$ 上一点，连接 $C E$ ， $D F ⊥ C E$ 于点 $F ， G D ⊥ D F ， A G ⊥ D G ， A G = C F$ ．求证：四边形 $A B C D$ 是正方形．
【实践探究】
（2）小慧受此问题启发，逆向思考并提出新的问题：如图2在正方形 $A B C D$ 中， $E$ 是边 $A B$ 上一点，连接 $C E ， D F ⊥ C E$ 于点 $F ， A H ⊥ C E$ 交 $C E$ 的延长线于点 $H ， D G ⊥ D F$ 于点 $D$ ，并交 $H A$ 延长线于点 $G$ ．猜想线段 $F H ， A H ， C F$ 的数量关系，并说明理由．
【拓展迁移】
（3）小贤深入研究小慧提出的这个问题，发现并提出新的探究点：如图3，在正方形 $A B C D$ 中， $E$ 是边 $A B$ 上一点，连接 $C E ， A H ⊥ C E$ 交 $C E$ 延长线于点 $H$ ，点 $M$ 在 $C H$ 上，且 $A H = H M$ ，连接 $A M$ ， $B H$ ，若 $B H = \sqrt{2}$ ，请直接写出 $C M$ 的长度．

查看解析
7、【素材1】在毕业晚会上，为了烘托晚会气氛，需要在晚会上悬挂一串彩灯，如图①．挂好后彩灯灯绳形状可近似看成由两段抛物线拼接而成．
【素材2】将图①的两段抛物线抽象成如图②所示的抛物线 $L_{1}$ 和抛物线 $L_{2}$ ，抛物线 $L_{1}$ 和抛物线 $L_{2}$ 大小形状完全相同， $A O$ ， $B C$ ， $D E$ 三个支撑杆均垂直于地面 $O E$ ，垂足分别是点 $O$ ， $C$ ， $E$ ， $A O = B C = D E = 3 m$ ．
【素材3】点C是 $O E$ 的中点， $O C = 4 m$ ．以点O为原点， $O E$ 所在直线为x轴， $O A$ 所在直线为y轴建立如图②所示的平面直角坐标系，抛物线 $L_{1}$ 的函数表达式为 $y = a x^{2} - b x + 6 b$ ．
【任务】

(1)、求 $a, b$ 的值；

(2)、求抛物线 $L_{2}$ 的函数表达式；

(3)、在抛物线 $L_{2}$ 的点M处绑一根竖直彩带（彩带绷直，打结处的长度忽略不计，抛物线的形状不改变），彩带末端恰好接触到地面N处， $M N ⊥ O E$ 于点 $N$ ， $N E = 3 m$ ，求彩带的长度 $M N$ ．

查看解析
8、如图， $B E$ 是 $⊙ O$ 的直径，点 $A$ ，点 $D$ 在 $⊙ O$ 上，且位于 $B E$ 的两侧，点 $C$ 在 $B E$ 的延长线上， $∠ E A C = ∠ A D E$ ．

(1)、求证： $C A$ 是 $⊙ O$ 的切线；

(2)、当 $A D$ 平分 $∠ B A E$ 时，若 $A C = 6 ， C E = 3$ ，求 $D E$ 的长．

查看解析
9、综合与实践
为响应国家“双碳”战略，某中学数学小组针对燃油汽车与新能源汽车的经济性展开课题研究．数学小组针对价格相近的国产燃油汽车与新能源汽车进行使用费用对比分析，探究其经济性差异．信息如表所示：
参数类型
燃油汽车
新能源汽车
能源类型
燃油
电能
能源容量
油箱容积： $50$ 升
电池电量： $50$ 千瓦时
能源价格
油价： $8$ 元/升
电价： $1$ 元/千瓦时
续航里程
$a$ 千米
$\frac{a}{2}$ 千米
据调查，燃油汽车的每千米行驶费用比新能源汽车多 $0.6$ 元，燃油汽车和新能源汽车每年的其它费用分别为 $4800$ 元和 $7500$ 元．
请按要求完成下列任务：

(1)、用含 $a$ 的代数式表示新能源汽车的每千米行驶费用；

(2)、分别求出燃油汽车和新能源汽车的每千米行驶费用；

(3)、每年行驶里程满足什么条件时，买新能源汽车的年费用比燃油汽车的年费用更低？（年费用 $=$ 年行驶费用 $+$ 年其它费用）

查看解析
10、为落实“阳光体育”活动要求，某校随机抽取20名学生，调查他们每天参加体育锻炼的时间（单位：分钟），锻炼时间在 $30 \leq x < 60$ 范围内的数据：35，40，50，45，50，30，45，55，40，50．结合以下统计表（图）信息回答下列问题：
不完整的统计表
锻炼时间 $x$ （分钟）
等级
人数
$0 \leq x < 15$
A
2
$15 \leq x < 30$
B
b
$30 \leq x < 60$
C
10
$x \geq 60$
D
$d$

(1)、统计表中 $b =$ ___________， $d =$ ___________；

(2)、统计图中 $C$ 等级对应扇形圆心角为___________度；

(3)、若全校共有1200名学生，估计锻炼时间达到 $C$ 等级及以上的学生人数有多少人？

查看解析
11、如图，在 $△ A B C$ 中， $A C = B C$ ，已知点 $D$ 是线段 $A B$ 的中点．

(1)、尺规作图：过点 $D$ 作 $A C$ 的平行线交 $B C$ 于点 $E$ ；（要求：保留作图痕迹，不写作法，标明字母）

(2)、在（1）所作的图中，连接 $C D$ ，若 $D E = 3 ， ∠ A = 30 °$ ，求 $C D$ 的长．

查看解析
12、（1）已知 $a = |- 2| + 3^{0} - \sqrt{4}$ ，计算 $a$ 的值；
（2）在（1）的条件下，先化简，后求值： $2 (a^{2} - 1) - a^{2} + 2$ ．

查看解析
13、如图，在矩形 $A B C D$ 中，点 $E$ 为 $A B$ 的中点， $P$ 为 $B C$ 边上的任意一点，把 $△ P B E$ 沿 $P E$ 折叠，得到 $△ P F E$ ，连接 $C F$ ．若 $A B = 5$ ， $B C = 6$ ，则 $C F$ 的最小值为．

查看解析
14、已知一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $(- 1, 3)$ ，且与 $y$ 轴交点的纵坐标为2，则它的解析式为．

查看解析
15、一个不透明的袋子里装有1个红球、1个白球和1个绿球，这些球除颜色外完全相同．小明随机从袋中摸出1个球，恰好摸到白球的概率是．

查看解析
16、比较大小： $- 1$ $2$ （填“ $>$ ”“ $<$ ”或“ $=$ ”）．

查看解析
17、如图，平面直角坐标系中，原点 $O$ 为正六边形 $A B C D E F$ 的中心， $E F ∥ x$ 轴，点 $E$ 在反比例函数 $y = \frac{k}{x}$ （ $k$ 为常数， $k > 0$ ）的图象上，将正六边形 $A B C D E F$ 向上平移 $\sqrt{6}$ 个单位长度，点 $D$ 恰好落在该函数图象上，则 $k$ 的值为（）

A、 $8 \sqrt{3}$ B、 $4 \sqrt{3}$ C、 $4 \sqrt{2}$ D、 $2 \sqrt{6}$

查看解析
18、《九章算术》是中国传统数学重要的著作之一，其中第九卷《勾股》中记载了一个“圆材埋壁”的问题：“今有圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”用几何语言表达为：如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点 $E ， E B = 1$ 寸， $C D = 10$ 寸，则直径 $A B$ 长为（）

A、 $6.5$ 寸 B、 $12$ 寸 C、 $13$ 寸 D、 $26$ 寸

查看解析
19、某公司研发的两个 $A I$ 模型 $R_{1}$ 和 $R_{2}$ 共同处理一批数据．已知 $R_{2}$ 单独处理数据的时间比 $R_{1}$ 多2小时．若两模型合作处理，仅需1.2小时即可完成．设 $R_{2}$ 单独处理需要 $x$ 小时，可列方程为（）

A、 $\frac{1}{x} + \frac{1}{x - 2} = 1.2$ B、 $\frac{1}{x} + \frac{1}{x + 2} = \frac{1}{1.2}$ C、 $\frac{1}{x} + \frac{1}{x - 2} = \frac{1}{1.2}$ D、 $x + (x + 2) = 1.2$

查看解析
20、小李在做“小孔成像”实验时，蜡烛到挡板的距离与挡板到屏幕的距离之比是 $6 : 13$ ．若烛焰 $A C$ 的高是 $3 cm$ ，则实像 $D B$ 的商是（）

A、 $6.5 cm$ B、 $13 cm$ C、 $26 cm$ D、 $39 cm$

查看解析

上一页 771 772 773 774 775 下一页跳转

参数类型	燃油汽车	新能源汽车
能源类型	燃油	电能
能源容量	油箱容积： $50$ 升	电池电量： $50$ 千瓦时
能源价格	油价： $8$ 元/升	电价： $1$ 元/千瓦时
续航里程	$a$ 千米	$\frac{a}{2}$ 千米

锻炼时间 $x$ （分钟）	等级	人数
$0 \leq x < 15$	A	2
$15 \leq x < 30$	B	b
$30 \leq x < 60$	C	10
$x \geq 60$	D	$d$