-
1、如图,将点向右平移1个单位长度,再向上平移2个单位长度,则所得点的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2、在学校开展的环保主题实践活动中,某小组的5位同学捡拾废弃塑料瓶的个数分别为5,6,7,8,7,这组数据的众数是( )A、5 B、6 C、7 D、8
-
3、如图,直线 , 直线分别与 , 相交, , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、截至2025年5月5日,国产动画电影《哪吒2》在全球范围内热映,票房表现强劲.据官方统计,其全球总票房突破元.这一成绩使其成为中国影史票房排名前列的电影之一、将数据用科学记数法表示为( )A、 B、 C、 D、
-
5、随着人工智能技术的普及,出现众多具有广泛影响力的人工智能应用,以下是一些常见人工智能应用的图案,其中属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
6、【问题情境】如图1,在矩形中, , . 在上取一点E, , 点F是边上的一个动点,以为一边作四边形 , 使点N落在边上,点M落在矩形内或其边上.
【知识技能】(1)如图1,当四边形是正方形时,的面积为_____;
【构建联系】(2)如图2,当四边形是菱形时,若 , 的面积为S,求S与x之间的函数解析式;
【拓展应用】(3)如图3,正方形是某小区旁一块边长为100米的空地,为了提升附近居民的生活环境,现要把这块空地及其周边打造成一个生态公园.按设计要求,为广场区域,正方形是休息区,是儿童娱乐区, , 点N在边的延长线上.为满足各区域及绿化用地,想让广场的面积尽可能小,求面积的最小值及这时点D到点E的距离.

-
7、【问题背景】如图1,在平面直角坐标系中,有一矩形 , , 对角线 , 相交于点 , , 反比例函数与矩形交于点H,G, .

【问题解决】
(1)、求反比例函数的解析式;(2)、求的值;(3)、如图2,过点作于点于点 , 求的值. -
8、“准、绳、规、矩”是我国古代使用的测量工具.一个简单结构的“矩”指两条边成直角的曲尺(如图1),它的两条边分别是a,b,中国古代的天文和数学著作《周髀算经》中简明扼要地阐述了“矩”的功能,如“偃矩以望高”就是把“矩”仰立放置可以测量物体的高度.如图2,从“矩”EFG的一端E处望向一根木杆(木杆的宽度忽略不计)的顶端B处,使视线通过“矩”的另一端G处,测得 , , 若“矩”的边 , 求木杆的长.

-
9、如图,已知线段a,h.
 (1)、求作: , 使 , 且 , 高;(尺规作图,不写作法,保留作图痕迹)(2)、若 , , 请求等腰三角形的腰长.
(1)、求作: , 使 , 且 , 高;(尺规作图,不写作法,保留作图痕迹)(2)、若 , , 请求等腰三角形的腰长. -
10、解不等式组: .
-
11、如图,正方形和正方形的边长分别是4和2,连接 , H是的中点,连接 , 则的长为 .

-
12、某种风衣每件按进价的1.8倍标价,再降价40元售出后,每件可以获得120元的利润,那么该种风衣每件的进价为元.
-
13、已知二次函数的图象如图所示,对称轴为直线 , 则下列结论正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O即跷跷板的中点到地面的距离是 , 当小明从水平位置上升时,小敏离地面的高度是( ).
 A、 B、 C、 D、
A、 B、 C、 D、 -
15、下列图形是正方体展开图的是( )A、
 B、
B、 C、
C、 D、
D、
-
16、石墨烯是现在世界上最薄的纳米材料,其理论厚度应为 , 用科学记数法表示为( )A、 B、 C、 D、
-
17、在平行四边形中,对角线交于点 , 是线段上一个动点(不与点重合),过点分别作的平行线,交于点 , 交于点 , 连接 .
 (1)、如图1,如果 , , 求证:;(2)、如图2,如果 , , 且与相似,求的值,并补全图形;(3)、如图3,如果 , 且射线过点A,求的度数.
(1)、如图1,如果 , , 求证:;(2)、如图2,如果 , , 且与相似,求的值,并补全图形;(3)、如图3,如果 , 且射线过点A,求的度数. -
18、【问题背景】如图1,已知是等腰三角形, , 为边BC上一动点,由点向运动,以点为圆心,为半径作半圆弧分别交于点 .
【数学思考】(1)求证:在点运动过程中,始终有;
(2)如图2,在点运动过程中,设为线段的中点,连接交半圆弧于点 , 当点H恰为的中点时,求此时线段OB的长度;
【拓展探索】(3)如图3,点在点与点重合时停止运动,若此时半圆弧与等腰三角形的腰交于另一点P,且四边形为等腰梯形,求等腰三角形顶角度数的取值范围.

-
19、综合与实践.
【主题】排球运动的数学建模.
【素材】①如图1,一名排球运动员在比赛中起跳扣球,球在出手后的飞行路线可以用函数刻画,其中y轴是球网所在的位置,x轴是水平地面,排球飞行的水平距离x(米)与其飞行的高度y(米)的变化规律如下表:
x
-2
0
…
y
3
2.92
…
②如图2所示,排球场地标准:长18米,宽9米,球网高度为2.24米.
【模型建立】(1)求素材①中函数的解析式及排球的落点A的坐标;
【模拟计算】(2)若在素材①中对方运动员在球网另一侧截击,假设截击后球的轨迹与原来轨迹关于过截击点平行于y轴的直线对称,求使排球刚好能过网的截击点到球网的距离.(结果保留根号)
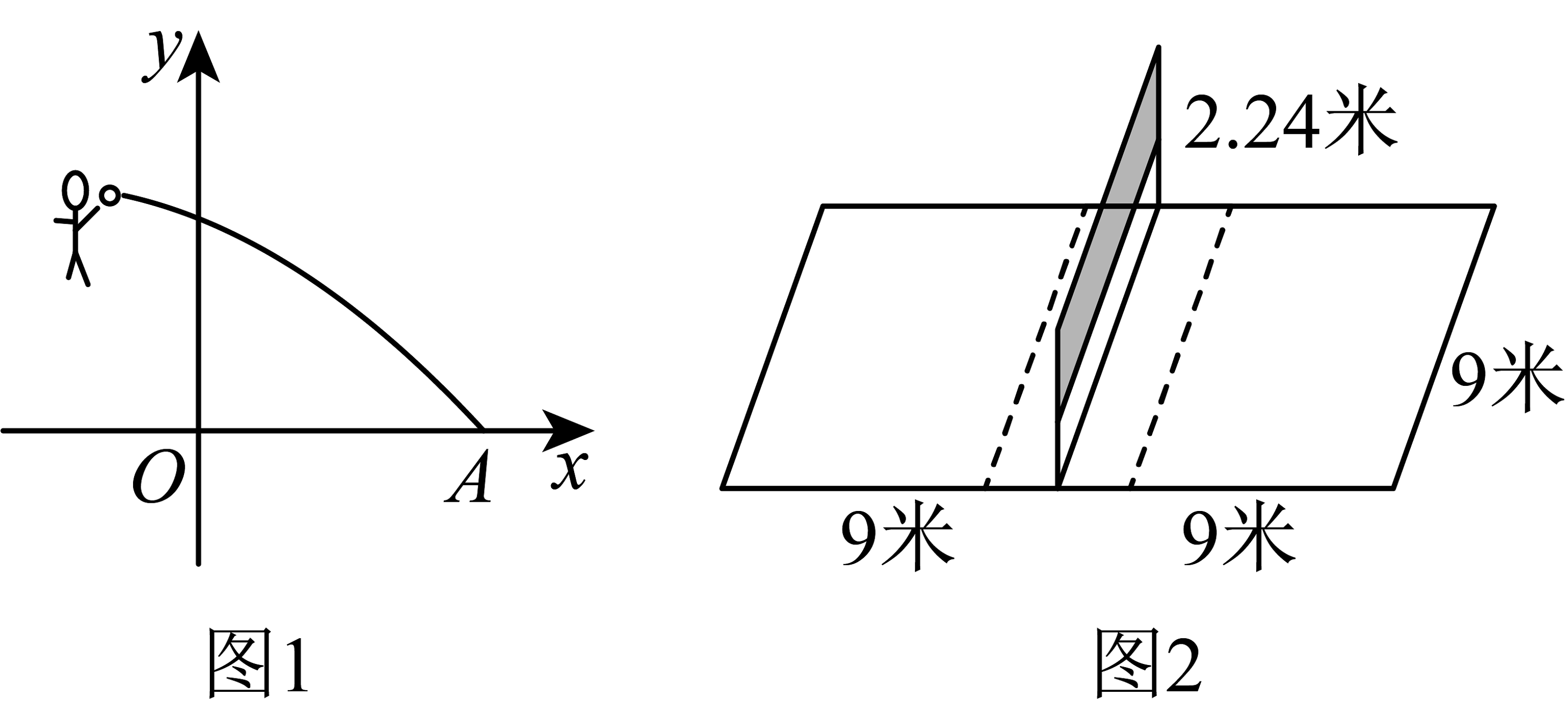
-
20、【阅读材料】给出如下定义:在平面直角坐标系中,点的纵坐标与横坐标的差“”称为点的“纵横差”.在某范围内某函数图象上所有点的“纵横差”中的最大值称为该范围内函数的“纵横极差”.例如:点的“纵横差”为;函数图象上所有点的“纵横差”可以表示为;当时,的最大值为 , 所以函数()的“纵横极差”为 .
【问题解决】根据阅读材料中的定义,解答下列问题:
(1)、求点的“纵横差”;(2)、求函数的“纵横极差”;(3)、若为实数,函数的“纵横极差”为 , 求的值.