-
1、 如图， 一个长方体形盒子的长为15cm， 宽为10cm， 高为20cm， 点B到点C的距离是5cm.一只蚂蚁沿盒的外表面从点A处爬到点B处，那么它爬行的最短路程是多少?
-
2、一架云梯长25m，如图那样斜靠在一面墙上.当这架云梯的顶端位于A处时，它的底端位于B处，底端离墙7m.
(1)、这架云梯的顶端到地面的距离是多少?(2)、当这架云梯的顶端从A处下滑4m到达处时，它的底端从B处滑动到 处，云梯底端在水平方向滑动的距离也是4m吗? -
3、(1)、已知直角三角形的三边长均为正整数，其中一直角边长为8，求这个直角三角形的另两边长；(2)、根据求解(1)的经验，尝试探索出更多的勾股数组.
-
4、如图 ①，直角三角形的两个锐角分别是40°和50°，它的三边上分别有一个正方形.执行下面的操作：分别以两个小正方形的边为斜边，向外作一个锐角为40°的直角三角形；再分别以所得到的直角三角形的直角边为边，向直角三角形外作正方形.图②是1次操作后得到的图形.
(1)、试画出2次操作后得到的图形.(2)、已知最初的直角三角形斜边长为1cm，写出2次操作后得到的图形中所有正方形的面积和.(3)、如果一直画下去，你能想象出它的样子吗?请借助数学软件进行探索.(4)、重复上述步骤若干次后得到的图形称为“毕达哥拉斯树”.如果最初的直角三角形是等腰直角三角形，那么此时“毕达哥拉斯树”会是什么形状? -
5、如图，方格纸上每个小正方形的面积为1个单位.
(1)、在方格纸上，以线段AB为边长画正方形，计算所画正方形的面积，并解释你的计算方法；(2)、请在图上分别画出面积为5个单位、10个单位、13个单位的正方形. -
6、据说古埃及人曾用下面的方法得到直角：如图所示，他们用13个等距的结把一根绳子分成等长的12段，一个人同时握住绳子的第1个结和第13个结，另两个人分别握住第4个结和第8个结，拉紧绳子，就会得到一个直角三角形，其直角顶点在第4个结处.请你说说其中的道理.
-
7、据传，当年毕达哥拉斯借助如图所示的两个图验证了勾股定理，请你说说其中的道理.
-
8、如图，直角三角形三边上的半圆面积之间有什么关系?
-
9、 如图， BC长为3cm， AB长为4cm， AF长为12cm.求正方形 CDEF的面积.
-
10、一只蚂蚁沿图中所示的折线由点A处爬到了点D处，它一共爬行了多少厘米(图中小方格的边长代表1cm)?
-
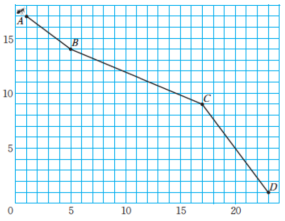
11、在一张纸上复制四个全等的直角三角形，并将四个三角形剪下来，通过拼图的方法验证勾股定理.你有哪些方法?说说你的方法与课堂上的方法之间有什么联系与区别.
-
12、如图，某储藏室入口的横截面是一个半径为1.2m的半圆，一个长、宽、高分别是1.2m，1m，0.8m的箱子能放进储藏室吗?
-
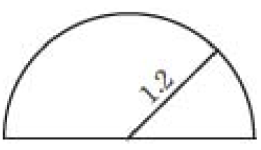
13、如图(单位：cm)，求等腰三角形ABC的面积.
-
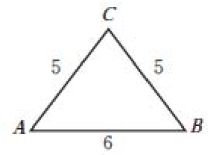
14、请用如图所示的图形验证勾股定理，并说一说这一方法与课堂上的方法之间的联系.
-
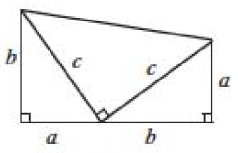
15、如图，所有的四边形都是正方形，所有的三角形都是直角三角形.请在图中找出若干图形，使得它们的面积之和恰好等于最大正方形①的面积，尝试给出两种以上的方案.
-
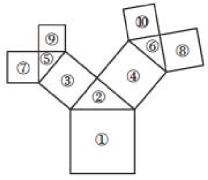
16、如图，强大的台风使一根旗杆在离地面3m 处折断倒下，旗杆顶部落在离旗杆底部4m处.旗杆折断之前有多高?
-
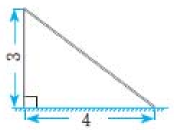
17、求斜边长为17cm、一条直角边长为15cm的直角三角形的面积.
-
18、求出图中直角三角形未知边的长度.
-
19、下图是某沿江地区交通平面图的一部分(单位：km)，为了加快经济发展，该地区拟修建一条连接 M，O，Q三城市的沿江高速公路，已知沿江高速公路的建设成本是5000万元/ km， 该沿江高速公路的建设成本预计是多少?
-
20、在一次军事演习中，红方侦察员王叔叔在距离一条东西向公路400m处侦察，发现一辆蓝方汽车在这条公路上疾驶.他用红外测距仪测得汽车与他相距400m；过了10s，测得汽车与他相距500m.你能帮王叔叔计算蓝方汽车这10s的平均速度吗?